6.1.1. Послідовності незалежних випробувань. Нехай здійснюється п незалежних випробувань, у кожному з яких подія А може відбутися зі сталою ймовірністю р, або не відбутися з ймовірністю q = 1 – p. Результат кожного випробування не залежить від результатів всіх попередніх випробувань, тобто випробування незалежні в сукупності. В цьому випадку говорять, що випробування здійснюються за схемою Бернуллі: В (п, р), де п і р – параметри схеми Бернуллі. Треба знайти ймовірність того, що в п випробуваннях подія А відбудеться к разів.
Подію в, яка полягає в тому, що подія А настала при кожному з к перших випробувань і не відбулася при інших (п – к) випробуваннях, можна записати у вигляді добутку к подій А (п – к) подій 
(6.1)
Оскільки всі п випробувань за умовою незалежні, то ймовірність настання події В дорівнює добутку ймовірностей настання подій А і А:
Р (В) = рk ·(1 – p) n - k = p k · q n - k .
6.1.2. Формула Бернуллі. Подія А може відбуватися k разів при п випробуваннях, але при цьому може утворитися послідовності (6.1). Проте для будь – якої такої послідовності подій ймовірність настання події А k разів при п випробуваннях дорівнює p k ·q n – k. Число найрізноманітніших послідовностей появи події А k разів в п випробуваннях дорівнює числу сполучень з п елементів по k. Оскільки різні послідовності з k елементів А і п – k елементів А можна розглядати як різні наслідки серії з п незалежних випробувань, то всі ці наслідки (події) несумісні. Тому шукану ймовірність, яку звичайно позначають Р п (k), обчислюють як суму ймовірностей настання різних наслідків серії з п випробувань:
P n (k) = C 
· pk · (1 – p) n - k = C · pk · qn - k .
Ця формула називається формулою Бернуллі.
6.1.3. Найвірогідніше число появи події А. Ймовірності Рп (к) при фіксованому п спочатку зростають при збільшенні k від 0 до деякого числа ko , а потім зменшуються, якщо ko < k 
n. Число ko, якому при заданому п відповідає найбільша ймовірність Рп (ko), називається найвірогіднішим числом появи події А. Якщо число р (п + 1) дробове, то ko = [p(n+1)] – цілій частині цього числа. Якщо р(п + 1) ціле,то ko має два значення р(п + 1) ціле, то ko має значення р(п + 1) і (п + 1) – 1.
6.1.4.Локальна теорема Муавра – Лапласа. Користуватися формулою Бернуллі (6.2.) при великих значеннях п досить важко. В таких випадках застосовують локальну теорему Мувра – Лапласа, яка дає асимптотичну формулу вигляду
Рп (k) 
· 
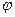(x), де 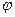(х) = 
е 
, х = 
.
Існують таблиці значень функції 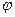(х) для додатних значень аргументу х (додаток 1). Для від’ємних значень аргументу використовують ті ж самі таблиці, оскільки функція 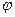(х) парна, тобто 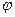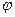(-х) = (х).
6.1.5. Інтегральна теорема Муавра – Лапласа. Щоб знайти ймовірність Рп (k1,k2) того, що кількість появи події А в п випробуваннях знаходиться в межах k1 k k2, використовують інтегральну теорему Муавра – Лапласа:
Pn (k 1, k 2) 
(6.4)
де 
Оскільки визначений інтеграл (6.4) не виражається через елементарні функції, то використовують таблиці, в яких вміщені значення функції Лапласа
для доданих значень аргументу х (додаток 2). Для від’ємних значень аргументу використовують ті ж самі таблиці, враховуючи, що функція Ф (х) непарна, тобто 
Щоб користуватися функцією Лапласа, перетворимо співвідношення (6.4)
Остаточно маємо
(6.5)
6.1.6.Розподіл Пуассона. Якщо у послідовності незалежних випробувань за схемою Бернуллі п досить велике, а р мале (р 
npq <9), то при обчисленні Рп (k) доцільно користуватися граничною формулою Пуассона (закон “рідкісних” явищ):
де 
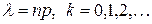(6.6)
Для відомих значень k і 
використовують таблиці функції (6.6)
(додаток 3).
