1.КОМБІНАТОРИКА
Нехай множина А містить n елементів. Множина А називається упорядкованою, якщо кожному її елементу поставлено у відповідність деяке натуральне число, тобто елементи занумеровані. Тут істотним є як набір елементів множини, так і порядок їх розташування.
Розміщеннями з n елементів по k (
) називаються упорядковані підмножини множини А, що містять k елементів, і які відрізняються одна від одної як складом елементів, так і порядком їх слідування.
Число розміщень із n елементів по k (записують 
) обчислюється за формулою
(1.1)
де n! називається n-факторіал і визначається за формулою
окрім того, за означенням
0!=1.
Перестановками називаються розміщення із n елементів по n.
Число перестановок із n елементів (записують 
) обчислюється за формулою
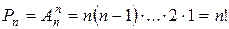(1.2)
Сполученнями (комбінаціями) із n елементів множини А по k називаються невпорядковані її підмножини, що містять k елементів, які відрізняються між собою хоча б одним елементом.
Число сполучень із n елементів по k (записують 
) обчислюється за формулою
(1.3)
Мають місце рівності
Нехай множина А складається з n елементів: А = 
. Розміщеннями з повтореннями називаються всі упорядковані k -елементні підмножини (взагалі кажучи, з повтореннями), які відрізняються або складом елементів, або порядком їх слідування. Наприклад, при k =4 множини 
є різними.
Число всіх розміщень з повтореннями з n елементів по k (записують 
) обчислюється за формулою
(1.4)
Нехай множина А містить n елементів k різних типів: n 1 елемент 1-го типу, n 2 елементів 2-го типу,..., nk елементів k -го типу, причому n 1+ n 2+…+ nk = n.
Перестановками з повтореннями такої множини А називаються будь-які упорядковані множини з n елементів, які можуть повторюватись.
Число всіх таких перестановок (записують Pn (n 1, n 2,… nk)) обчислюється за формулою
Pn (n 1, n 2,… nk)= 
Сполученнями з повтореннями називаються невпорядковані k -елементні підмножини (взагалі кажучи, з повтореннями), які відрізняються складом елементів. Наприклад, при k = 4 набори 
є однаковими для даного експерименту, а набір 
відрізняється від двох попередніх.
Число сполучень з повтореннями із n елементів по k (записують 
) обчислюється за формулою
(1.6)
При розв'язанні задач комбінаторики використовують такі правила.
Правило суми. Якщо деякий об'єкт А можна вибрати з сукупності об'єктів m способами, а інший об'єкт В можна вибрати n способами, то вибрати або А, або В можна m + n способами.
Правило добутку. Якщо деякий об'єкт А можна вибрати з сукупності об'єктів m способами і після кожного такого вибору об'єкт В можна вибрати n способами, то пару об'єктів (А, В) можна вибрати m× n способами.
