Цель работы: вычисление интегралов в задачах геометрии и механики в программе MathCad.
Указания к выполнению лабораторной работы:
I Вычислить площадь плоской фигуры, ограниченной заданными линиями.
1 Записать уравнение кривых, которые ограничивают площадь плоской фигуры.
2 Найти точки их пересечения, для того чтобы использовать их у двукратном интегрировании.
3 Обратиться на панели Символы к функции simplify.
4 Ввести оператор интегрирования. В соответствующих местах заполнить имя первой переменной и границы интегрирования.
5 На месте ввода функции под интегралом ввести еще один оператор интегрирования, границы интегрирования и подынтегральную функцию
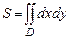
II Вычислить координаты центру тяжести пластины.
1 Записать уравнения кривых, которые описывают область D пластины.
2 Найти точки их пересечения, для того чтобы использовать их в двукратном интегрировании.
3 Найти площадь S однородной пластинки через двойной интеграл.
3.1 Обратиться на панели Символы к функции simplify.
3.2 Ввести оператор интегрирования. В соответствующих местах заполнить имя первой переменной и границы интегрирования.
3.3 На месте ввода функции под интегралом ввести еще один оператор интегрирования, границы интегрирования и подынтегральную функцию
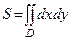
4 Найти аналогично статические моменты Mx и My пластины относительно осей Ох и Оу как двойные интегралы
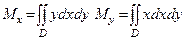
5 Определить координаты центра тяжести как отношение подынтегральной функции, которая определяет статические моменты пластины относительно осей Ох и Оу
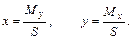

Таблица 7.1 – Варианты задания к лабораторной работе №7
| Номер варианта | Функции для вычисления площади фигуры | Функции для вычисления координат центра тяжести фигуры |
| x=y2-2y; x+y=0 | 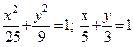
| |
| y=2-x; y2=4x+4 | y=x2; y=2x2; x=1;x=2 | |
| y2=4x-4; y2=2x (извне параболы) | y2=x; x2=y | |
| 3y2=25x; 5x2=9y | y= 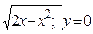
| |
| y2+2y-3x+1=0; 3x-3y-7=0 | 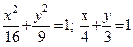
| |
| y=4x-4x2; y=x2-5x | 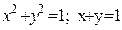
| |
| x=4-y2; x+2y-4=0 | 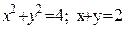
| |
| y2=4(x-1); x2+ y2=4 (извне параболы) | 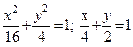
| |
| x=y2-2y; x+y=0 | 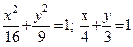
| |
| y=2-x; y2=4x+4 | 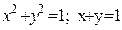
| |
| y2+2y-3x+1=0; 3x-3y-7=0 | 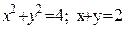
| |
| y=4x-4x2; y=x2-5x | y2=x; x2=y | |
| x=4-y2; x+2y-4=0 | y= 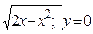
| |
| x=y2-2y; x+y=0 | 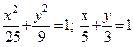
| |
| y=2-x; y2=4x+4 | y=x2; y=2x2; x=1;x=2 | |
| y2+2y-3x+1=0; 3x-3y-7=0 | 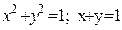
| |
| y=4x-4x2; y=x2-5x | 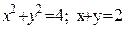
| |
| x=4-y2; x+2y-4=0 | 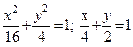
| |
| x=y2-2y; x+y=0 | 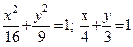
| |
| y=2-x; y2=4x+4 | 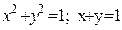
| |
| y2=4(x-1); x2+ y2=4 (извне параболы) | 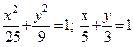
| |
| y=2-x; y2=4x+4 | y=x2; y=2x2; x=1;x=2 |
Продолжение табл. 7.1
| y2=4x-4; y2=2x (извне параболы) | y2=x; x2=y | |||
| x=y2-2y; x+y=0 | y= 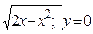
| |||
| y=2-x; y2=4x+4 | 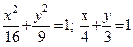
| |||
| 3y2=25x; 5x2=9y | 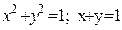
| |||
| x=y2-2y; x+y=0 | 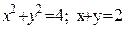
| |||
| y2+2y-3x+1=0; 3x-3y-7=0 | 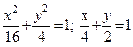
| |||
| y=4x-4x2; y=x2-5x | y=x2; y=2x2; x=1;x=2 | |||
| x=4-y2; x+2y-4=0 | y2=x; x2=y | |||
Пример
I Вычислить площадь фигуры, которая ограничена линиями x=4y-y2 и x+y=6.
1 Найти координаты точек пересечения заданных линий, для чего необходимо решить систему уравнений (одной из встроенных функций MathCad, графически или решить систему уравнений).
x=4y-y2
x+y=6.
В результате будут получены точки пересечения А(4;2) и В(3;3).
2 Записать формулу для вычисления площади через кратный интеграл и использовать на панели Символы функцию simplify
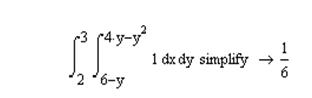 .
.
II Вычислить координаты центра тяжести пластины, которая ограничена кривыми y2=4x+4 i y2=-2x+4.
Площадь
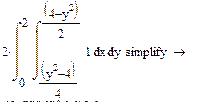
Статические моменты относительно осей Ох и Оу
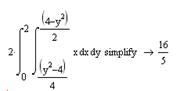
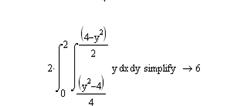
Координаты центра тяжести
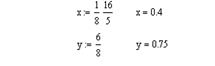
Контрольные вопросы
1 Какие геометрические характеристики можно вычислить с использованием интегралов?
2 Как вычислить центр тяжести через интегралы?






