Цель работы: вычисление производных в задачах геометрии и нахождение частных производных высоких порядков в программе MathCad.
Указания к выполнению лабораторной работы:
I Составить уравнение касательной и нормали к линии, которая задана уравнением y(x)=f(x) в точке М(x0,y0).
1 Задать значения х0 и у0 в точке М.
2 Записать уравнение линии у(х).
3 Определить производную от функции у(х)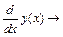 
, использовав панель вычислений и панель символов. Присвоить значение производной функции уу(х): = 
.
4. Записать уравнение касательной у виде
,
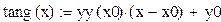5. Аналогично записать уравнение нормали 
6. Построить графики касательной и нормали.
7 Отформатировать графики.
II Выполнить числовое и символьное вычисление частных производных высшего порядка от функции трех переменных.
1 Записать функцию, от которой будут вычисляться производные второго порядка.
2 Обратиться к панели вычислений и выбрать оператор дифференцирования.
3 В соответствующем месте заполнения оператора записать функцию, переменную для дифференцирования и порядок дифференцирования.
4 Нажать правой кнопкой мыши на знак оператора дифференцирования и в контекстному меню выбрать View Derivative As (Показать производную как), установить флажок Partial Derivative (Частная производная).
5 Отметить оператор дифференцирования и обратиться к панели Символика/Вычислить/В символах.
6 Задать числовые значения для переменных, от которых вычисляется производная.
7 Вычислить числовые значения производных.
Таблица 6.1 – Варианты заданий к лабораторной работе №6
| Номер варианта | Функция f(x) для определения касательной и нормали | Точка М (х0,у0) для определения касательной и нормали | Функция f(x,у,z) для вычисления частной производной | Точка М (х0,у0,z0) для числового вычисления частной производной | ||||
| х2 -3х+5 | (2,3) | х2 -3х3y-4y2+2y-z3 | (0,1,2) | |||||
| х2 +2х+6 | (-1.1) | z2ex*x+y*y | (0,0,0) | |||||
| х3-3х2 | (3,1) | xcos(y)+yz4 | (1,0,0) | |||||
| 0.5х-sin(x) | (0, p/3) | z ln (x2-y2) | (3,1,3) | |||||
| (x-5)ex | (4,0) | zsin(xy)+z2 | (1,1,1) | |||||
| 1-(x-2)4/5 | (2,1) | х2 +2y2-3xy-4z2 | (0,0,0) | |||||
| x5+5x-6 | (0,-1) | zx× ln (y)+xy2z | (0,2,1) | |||||
| (x3+4)/x2 | (2,3) | y(x-zcos(x)) | (0,0,0) | |||||
| (0,1) | sin(x)(cos(z)+cos(y)) | (1,0,0) | |||||
| sin2(x) | (0.5,0.5) | x4yz+sin(y) | (2,1,0) | |||||
| x2-0.5x4 | (0,0) | (x-y2)*(z3-x) | (1,1,1) | |||||
| х3-3х2 | (0, p/3) | х2 -3х3y-4y2+2y-z3 | (0,1,2) | |||||
| 0.5х-sin(x) | (4,0) | z2ex*x+y*y | (0,0,0) | |||||
| (x-5)ex | (2,1) | xcos(y)+yz4 | (1,1,1) | |||||
| 1-(x-2)4/5 | (2,1) | z ln (x2-y2) | (3,1,3) | |||||
| x5+5x-6 | (0,-1) | zsin(xy)+z2 | (1,1,1) | |||||
| 0.5х-sin(x) | (0, p/3) | х2 +2y2-3xy-4z2 | (0,0,0) | |||||
| (x-5)ex | (4,0) | zx× ln (y)+xy2z | (0,2,1) | |||||
Продолжение табл. 6.1
| 1-(x-2)4/5 | (2,1) | y(x-zcos(x)) | (0,0,0) | |||||
| x5+5x-6 | (0,-1) | sin(x)(cos(z)+cos(y)) | (1,0,0) | |||||
| (x3+4)/x2 | (2,3) | zx× ln (y)+xy2z | (0,2,1) | |||||
| х3-3х2 | (3,1) | y(x-zcos(x)) | (0,0,0) | |||||
| 0.5х-sin(x) | (0, p/3) | sin(x)(cos(z)+cos(y)) | (1,0,0) | |||||
| (x-5)ex | (4,0) | x4yz+sin(y) | (2,1,0) | |||||
| 1-(x-2)4/5 | (2,1) | (x-y2)*(z3-x) | (1,1,1) | |||||
| x5+5x-6 | (0,-1) | х2 -3х3y-4y2+2y-z3 | (0,1,2) | |||||
| (x3+4)/x2 | (2,3) | z2ex*x+y*y | (0,0,0) | |||||
|
| (0,1) | xcos(y)+yz4 | (1,0,0) | |||||
| sin2(x) | (0.5,0.5) | z ln (x2-y2) | (3,1,3) | |||||
| x2-0.5x4 | (0,0) | zsin(xy)+z2 | (1,1,1) | |||||
Пример
I Составить уравнение касательной и нормали к линии, которая задана уравнением y(x)=х4 -3х3+4х2-5х+1 в точке М(0,1).
1 Задать значения х0 и у0 в точке М: х0:=0, у0:=1.
2 Записать уравнения лини у(х):= х4 -3х3+4х2-5х+1.
3 Определить производную от функции у(х) 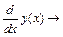, использовав панель вычислений и панель символов. Присвоить значение производной функции уу(х): = .
4 Записать уравнение касательной в виде
,
 .
|
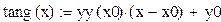5 Аналогично записать уравнение нормали
|
|
6 Построить графики касательной и нормали.
7 Отформатировать графики.
|
|
|
|
|
|
|
|
|
|
|
|
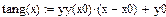
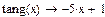
Рисунок 24- График касательной и нормали
ІІ Записать функцию, от которой будут вычисляться производные второго порядку
2 Обратиться к панели вычислений и выбрать оператор дифференцирования 
.
3 В соответствующие места заполнения оператора записать функцию, переменную для дифференцирования и порядок дифференцирования.
4 Нажать правой кнопкой мыши на знак оператора дифференцирования и в контекстному меню выбрать View Derivative As (Показать производную как), установить флажок Partial Derivative (Частная производная) (рис.25):
, 
, 
.
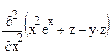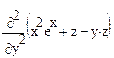5 Отметить оператор дифференцирования и обратиться к панели Символика/Вычислить/В символах.
6 Задать числовые значения для переменных, от которых вычисляется производная х:=1, y:=1, z:=1.
7 Вычислить числовые значения производных.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 25 – Диалоговое окно Показать производную
Контрольные вопросы
1 Як найти касательную к любой кривой в MathCad?
2 Як найти нормаль к любой кривой в MathCad?
3 Як выполнить символьные вычисления частных производных высокого порядка?
4 Як выполнить числовые вычисления частных производных высокого порядка?
