Угол сдвига и угол резания формируют площадки, по которым происходит движение срезанного грунта, а, следовательно, и направления действия сил, зависящие от положения этих площадок.
Граничные условия на дневной поверхности разрабатываемого грунта будут определяться всесторонним давлением связности.
Определим граничные условия на площадке сдвига. Для этого необходимо найти значения сил, действующих на поверхность площадки сдвига ОВВ1O1.
Рассмотрим силы, действующие на грунт, перемещаемый по ножу (рисунок 4.7) при свободном резании, то есть без учета сопротивлений, возникающих по боковым кромкам ножа, так как эти сопротивления оказывают локальное воздействие на грунт по торцам ножа. По этой причине они практически не изменяют граничные условия на поверхности площадки сдвига ОВВ1O1. Будем считать так же, что на данном этапе расчетное положение площадки сдвига определено.
На призму грунта с нормальным сечением ОВКД действует, прежде всего, ее собственный вес, равный
. (4.38)
Объем грунта V, входящий в эту формулу, определяется по уравнению (4.22).
Со стороны ножа действуют нормальная сила N и сила трения Т, равная
, (4.39)
где 
- угол внешнего трения.
Сила N расположена в плоскости XOY, а сила Т ориентирована против направления движения грунта по ножу, т. е. направлена в сторону движения грунта. В плоскости XOY будет расположена ее проекция T’, равная
. (4.40)
Угол 
, входящий в это уравнение, находится по формуле (4.7).
Со стороны площадки сдвига ОВB1O1 на перемещаемый по ножу грунт действуют нормальная сила Q, сила трения S и сила CОВ, затрачиваемая на преодоление сцепления по площадке сдвига.
Нормальная сила Q так же расположена в плоскости XOY. Сила трения S и сила CОВ будут действовать в направлении, противоположном направлению сдвига грунта по площадке ОВB1O1. Этот сдвиг происходит под углом 
, на данном этапе неизвестном, но величина которого связана с углами сдвига 
и 
формулой (4.17).
Сила трения S будет равна
. (4.41)
Величина силы CОВ определится по формуле
, (4.42)
|
|
| Рисунок 4.7 – Расчетная схема сил: а) – полная; б) – в плоскости XOY. |
где 
- площадь лобовой площадки сдвига, определяемая по уравнению (4.37).
В плоскости XOY (рисунок 4.7, б) будут находиться проекции 
и 
рассмотренных выше сил, равные
;
. (4.43)
Составим уравнения проекций сил, действующих на перемещаемый по ножу срезанный грунт, на координатные оси X, Y и Z, учитывая, что ось Z расположена вдоль режущей кромки ножа
;
; 
.
Выразив силы трения Т и S через нормальные силы N и Q, придем к следующей системе уравнений
;
;
;
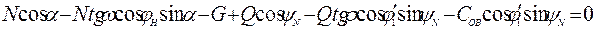Сгруппировав элементы системы уравнений, получим
;
Введя обозначения
;
;
; (4.45)
придем к системе
;
; (4.46)
;
В эту систему входят три неизвестных- силы N, Q и угол 
. Поскольку система состоит из трех уравнений и содержит три неизвестных, то такая система имеет решение.
Из третьего уравнения системы (4.44) можно получить, что
. (4.47)
Из первого уравнения системы (4.44) получим
. (4.48)
Подставляя это значение во второе уравнение, будем иметь после преобразований
,
откуда получим
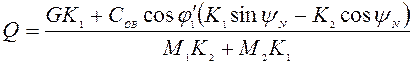. (4.49)
Поскольку решение нельзя представить в замкнутом виде, систему уравнений (4.46) необходимо решать численными методами. По завершении расчетов будем иметь значения угла и сил N и Q, а, следовательно, и зависящих от них сил трения T и S.
Для определения приведенного давления qmax, действующего на площадку сдвига, воспользуемся схемой, изображенной на рисунке 4.8. Обозначим на этой схеме давления от сил Q, S и CОВ соответственно как qQ, s и c, отметив при этом, что величина c будет являться удельным сцеплением грунта, что видно из уравнения (4.42).
Из схемы на рисунке 4.8 можно записать, что величина приведенного давления qmax будет равна
|
| Рисунок 4.8 – Схема к определению приведенного давления. |
. (4.50)
Отметим при этом, что
. (4.51)
Таким образом, приведенная методика расчета граничных условий и ее основное уравнение (4.50) позволяют получить величину приведенного давления, действующего на площадку сдвига при известном ее положении.
Устойчивость откоса будет минимальной, когда приведенное давление qmax наклонено к вершине откоса под углом внутреннего трения, что бывает в момент сдвига в направлении, совпадающем с направлением сдвига грунта.
Поэтому необходимо связать угол сдвига, измеренный в плоскости, нормальной к поверхности площадки сдвига и отклоненной от нормали к режущей кромке под углом , с нормальным углом сдвига 
. Для этого поступим следующим образом.
Проведем через точку О нормаль ОР к поверхности ОВВ1О1, являющейся площадкой сдвига (рис. 4.9). Через эту нормаль проведем секущую плоскость, перпендикулярную отрезку ВВ1, являющемуся режущей кромкой ножа. Таким образом, получим прямоугольный треугольник с прямым углом РОВ. Теперь повернем секущую плоскость на угол , получив при этом треугольник РОВ’. Отметим, что плоскость по-прежнему проходит через нормаль ОР, то есть она остается перпендикулярной поверхности сдвига ОВВ1О1. При этом длина отрезка 
, расположенного на поверхности сдвига, равна длине отрезка 
(формула 4.13). Новое обозначение 
введено лишь по той причине, что секущая плоскость на рисунке 4.9 перпендикулярна поверхности сдвига ОВВ1О1, в отличие от секущей плоскости на рисунке 4.2, проходящей через такой же отрезок, но перпендикулярной основанию плоскости, расположенному в горизонтальной плоскости. На рисунке 4.9 секущая плоскость, перпендикулярная основанию плоскости, представлена треугольником ОО′В′.
Таким образом, 
.
|
| Рисунок 4.9 – Схема для определения расчетного угла сдвига |
Из схемы видно, что из треугольников ОРВ и ОРВ’ соответственно будем иметь
;
, (4.52)
так как углы РОВ и РОВ’ являются прямыми, как углы между нормалью РО и любым лучом, проведенным в плоскости, перпендикулярной нормали.
Из формул (4.52) получим
. (4.53)
Полученное уравнение позволяет связать расчетный угол сдвига 
с углом сдвига измеренным в плоскости, нормальной к режущей кромке ножа.
Система уравнений решается итерационными методами. Суть расчета сводится к произвольному выбору предварительного значения угла сдвига 
и определения по уравнению (4.50) давления qmax на площадку сдвига. После этого определяется по одному из уравнений (2.45) или (2.47) угол сдвига, выдерживающий это давление. Полученное значение сравнивается с предварительно выбранным, и, если они не равны друг другу, то необходимо соответствующим образом выбрать новое значение угла 
и повторять расчеты до получения результата с требуемой точностью.
Определение сопротивлений
При косом резании грунта
Определим силы, действующие на нож.
При известной величине угла сдвига значения всех отмеченных выше сил будут известны. Для определения составляющих сопротивления резанию из этих сил достаточно использовать только силы 
N и Т, действующие как со стороны ножа на грунт, так и со стороны грунта на нож (уравнения (4.39) и (4.48)). Эти силы ориентированы по-разному. Сила N направлена перпендикулярно плоскости ножа, а сила Т, расположена в плоскости ножа и действует в направлении движения грунта по ножу, совпадающем с направлением перемещения ножа.
Силу N необходимо разложить по координатным осям X, Y и Z, изображенным на рисунок 4.7.
Нормальная проекция Nу силы N будет равна
. (4.54)
Это уравнение не изменяется при повороте ножа на угол 
в плане.
Горизонтальная проекция этой силы
. (4.55)
Угол между этой силой и осью Х является углом 
поворота ножа в плане. Поэтому касательная проекция Nх силы N будет равна
. (4.56)
Аналогичным образом получим и поперечную проекцию Nz
. (4.57)
Перейдем к сопротивлению резанию. В момент сдвига сопротивление будет максимальным, и его составляющие определятся таким образом
;
;
. (4.58)
При сдвиге разрушается сцепление на площадке сдвига. После сдвига значения сил N и Т, равно как и сил Q и S уменьшаются. При этом следует учесть, что грунт движется по сформированной площадке и в направлении, сформированном в момент сдвига. Поэтому, пренебрегая остаточным сцеплением, величину силы Qmin можно найти из уравнения (4.49) при СОВ=0, а именно
, (4.59)
а величину силы Nmin - уравнения (4.48) с учетом полученного значения Qmin.
. (4.60)
Сила трения Тmin, действующая после сдвига, будет равна
. (4.61)
Величину составляющих, действующих непосредственно после сдвига, можно получить из уравнений (4.58), подставляя в них значения Nmin и Тmin из уравнений (4.60) и (4.61) соответственно.
Будем иметь
;
; (4.62)
.
Максимальная величина амплитуды колебаний составляющих сопротивления резанию будет соответствовать большому сдвигу, при котором размеры площадки сдвига, а, следовательно, и значение силы СОВ будут максимальными. В итоге имеем
;
; (4.63)
.
Перейдем к определению сопротивлений по боковым граням ножа. Предельные касательные напряжения на боковой грани в момент сдвига определим по формуле Кулона (1.2), которая будет выглядеть так
, (4.64)
поскольку нормальные давления, действующие на грунт по боковым граням, можно найти так
, (4.65)
где 
- давление от нормальной силы Q, определяемое по уравнению (4.51).
Сдвигу боковой грани относительно массива препятствует сила 
(рисунок 4.10), действующая параллельно площадке сдвига О1В1 и равная
, (4.66)
где St - площадь боковой площадки сдвига О1В1С1.
Величину этой площади можно найти из рисунка 4.5 на основе следующих рассуждений. Длина отрезка В1О1 определится по первому уравнению (4.13), обозначенная в этом уравнении как 
. Длина отрезка В1С1, которую обозначим 
, будет равна
. (4.67)
Если длина отрезка ОС на рисунке 4.5 (б) будет равна
, (4.68)
то длина отрезка О1С1, которую обозначим как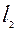 
, будет равна
, (4.69)
где 
определяется по формуле (4.23).
Тогда площадь 
можно найти по трем сторонам треугольника О1В1С1.
, (4.70)
где
. (4.71)
После сдвига произойдет разрушение сцепления, и величина силы 
уменьшается. Для этого случая, подставляя в формулу (4.51) значение Qmin из формулы (4.59), получим
. (4.72)
Поскольку свойства грунта, перемещаемого по ножу, практически не изменятся за малый промежуток времени, то значения коэффициента бокового давления 
так же не изменятся, а уравнение (4.65) будет выглядеть так
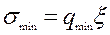. (4.73)
Тогда, при с=0, касательные напряжения станут равными
. (4.74)
И, наконец,
. (4.75)
Таким образом, по двум боковым граням ножа действуют дополнительные сопротивления, величина каждого из которых в момент сдвига определится по уравнению (4.66), а сразу после сдвига – по уравнению (4.75).
Эти силы действуют параллельно лобовой площадке сдвига в направлении отрезка В1О1, что видно из рисунка 4.10. Проекции этих сил на принятые раньше координатные оси с учетом рисунка 4.2 найдем следующим образом. Для силы 
;
; (4.76)
.
Аналогично для силы 
, действующей сразу после сдвига, будем иметь
;
; (4.77)
.
|
| Рисунок 4.10 – Схема для определения сопротивлений, возникающих по боковым граням. |
Тогда, с учетом сил 
и 
, уравнения (4.58) будут иметь следующий вид
;
; (4.78)
;
а уравнения (4.62) станут такими
;
; (4.79)
;
И, наконец, максимальную амплитуду колебаний с учетом сопротивлений по лобовым и боковым сторонам ножа можно найти, используя эти уравнения (4.78) и (4.79)
;
; (4.80)
.
Таким образом, определены все силовые параметры, характеризующие процесс косого резания.
Отметим, что изложенная методика расчета косого резания при φ=0 тождественна методике расчета лобового резания.
