Тренд і сезонні коливання продажу безалкогольних напоїв

Рік	Квартал	Млн дкл, yt	Тренд Yt	Індекс сезонності	Тренд, скоригований на сезоність, Yt =
		24,4	40,3	0,606	27,7
		52,6	41,7	1,262	51,0
		60,4	43,1	1,401	59,0
		34,0	44,6	0,763	32,1
		32,7	46,0	0,711	31,6
		56,2	47,5	1,184	58,0
		67,3	48,9	1,377	66,9
		36,2	50,4	0,719	36,1
		37,8	51,8	0,730	35,6
		65,3	53,3	1,225	65,1
		73,1	54,7	1,337	74,9
		38,4	56,1	0,689	40,4
Разом	´	578,4	578,4		578,4

Середньозважені індекси сезонності (для яких ваги — середньорічні обсяги продажу) становлять:

Для першого кварталу

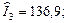Аналогічно розраховані індекси для другого кварталу для третього для четвертого .

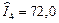Скоригований на сезонність тренд наведено в останній графі табл. 8.6. Для першого кварталу 1997 р.

.

Відхилення фактичних рівнів y_t від скоригованих трендів зумовлено дією випадкових причин.

Абсолютною мірою випадкових коливань є середнєквадратичне відхилення , яке обчислюється на основі залишкової дисперсії:

.

За даними табл. 8.7 залишкова дисперсія продажу безалкогольних напоїв становить

звідки .

Таблиця 8.7

ДО РОЗРАХУНКУ ЗАЛИШКОВОЇ ДИСПЕРСІЇ

t	yt
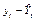
–5,5	24,4	27,7	–3,3	10,89
–4,5	52,6	51,0	1,6	2,56
–3,5	60,4	59,0	1,4	1,96
–2,5	34,0	32,1	1,9	3,61
–1,5	32,7	31,6	1,1	1,21
–0,5	56,2	58,0	–1,8	3,24
0,5	67,3	66,9	0,4	0,16
1,5	36,2	36,1	0,1	0,01
2,5	37,8	35,6	2,2	4,84
3,5	65,3	65,1	0,2	0,04
4,5	73,1	74,9	–1,8	3,24
5,5	38,4	40,4	–2,0	4,00
Разом	578,4	578,4		35,76

Поряд з абсолютною мірою випадкових коливань використовують відносну — коефіцієнт варіації V_е = 100 , де 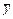— середній рівень динамічного ряду. Щодо випадкових коливань продажу безалкогольних напоїв, то

.

Різницю 100 – 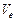використовують для оцінки сталості динаміки. У розглянутому прикладі ця різниця наближається до 100%, що свідчить про сталий характер тенденції і сезонних коливань реалізації безалкогольних напоїв.

Тема 9. Індекси

План

1. Суть та функції індексів.

2. Методологічні основи побудови зведених індексів.

3. Агрегатна форма індексів.

4. Середньозважені індекси.

5. Взаємозв’язки індексів.

6. Індекси середніх величин.

 

9.1. Суть і функції індексів

 

Термін індекс (index)є синонімом певної узагальнюючої характеристики. Наприклад, індекс реальних доходів населення за рік, індекс курсової вартості цінних паперів за місяць, регіональний індекс злочинності тощо. Кожний індекс є співвідношенням двох значень показника, який індексується: оціночного (поточного) і взятого за базу порівняння. Тобто за статистичною природою індекс — це відносна величина, яка характеризує зміну соціально-економічного явища в часі чи просторі або ступінь відхилення значення показника від певного стандарту (нормативу, середньої). Форми вираження індексу: коефіцієнти, проценти, промілле.

Історично індекси створювались як інструмент вивчення динаміки споживчих цін. Ще на початку XVII ст. англійський купець Т. Ман доводив переваги торгівлі з Індією, порівнюючи вартість товарів, які ввозились в Англію з Індії і Туреччини (шовк-сирець, прянощі тощо), за цінами індійськими та турецькими. Індекс цін становив 0,33, тобто закупівля зазначених товарів у Індії втричі дешевша порівняно з Туреччиною. Різницю вартостей Т. Ман визначив як суму економії від заміни торгового партнера. Такого роду розрахунки й досі вважаються найбільш логічним вираженням індексів.

Поступово коло показників, що піддавалися індексному аналізу, розширювалось, а методи аналізу вдосконалювались.

Індекс, як і будь-який статистичний показник, поєднує в собі якісний та кількісний аспекти. Назва індексу відбиває соціально-економічний зміст показника, числове його значення — інтенсивність змін або ступінь відхилення (індекс урожайності — 1,07, індекс продуктивності праці в галузі — 1,15 тощо).

Методика розрахунку (модель) індексу залежить від мети дослідження, статистичної природи показника, ступеня агрегованості інформації. Мета дослідження, зокрема, визначає функцію, яку виконує індекс у конкретному аналізі, та характер порівнянь.

Розрізняють дві функції індексів:

1) синтетичну, пов’язану з побудовою узагальнюючих характеристик динаміки чи просторових порівнянь;

2) аналітичну, спрямовану на вивчення закономірностей динаміки, взаємозв’язків між показниками, структурних зрушень.

Так, індексний факторний аналіз передбачає оцінку впливу факторів на динаміку показника, який індексується; індексні ряди є основою моніторингу динамічних соціально-економічних явищ, кон’юнктури ринку тощо.

Очевидно, що синтетична та аналітична функції індексів взаємозв’язані. Часто один і той самий індекс виконує обидві функції. Наприклад, індекс споживчих цін за рік становив 1,025. З одного боку, він характеризує середній приріст цін на 2,5%, а з іншого — свідчить про те, що за рахунок зростання цін вартість споживчого кошика зросла на 2,5%.

За характером порівнянь (у часі, просторі, з певним стандартом) індекси поділяються на динамічні, територіальні, міжгрупові. Динамічний індекс характеризує інтенсивність динаміки; при його розрахунку базою порівняння є одне з попередніх значень показника. База порівняння ідентифікується підрядковою позначкою «0», поточне значення показника — «1».

При просторових порівняннях визначається ступінь відхилення значень показника у просторі — між об’єктами, країнами, регіонами, які ідентифікуються певними літерами; вибір бази порівняння довільний. Міжгруповий індекс характеризує відхилення від певного стандарту (еталонного, максимального чи мінімального значення) або від середнього рівня по сукупності в цілому.

Визначальними ознаками інформаційної бази індексного аналізу є ступінь агрегованості та статистична природа показника. За ступенем агрегованості інформації індекси поділяються на індивідуальні та зведені. Вони позначаються відповідно символами i та I.Індивідуальні індекси характеризують співвідношення рівнів показника окремих елементів сукупності, зведені — певної множини елементів. У структурованій сукупності зведений індекс може бути груповим (субіндексом) або загальним (тотальним). Наприклад, в ієрархії динамічних індексів промислового виробництва динаміку обсягів окремих видів продукції (чавун, електроенергія, верстати) характеризують індивідуальні індекси, окремих галузей промисловості (металургія, енергетика, машинобудування) — субіндекси, промисловості в цілому — загальний індекс.

Показник, динаміку чи співвідношення якого характеризує індекс, називають індексованою величиною, йому надається певний символ. Наприклад, індивідуальний індекс фізичного обсягу продукції позначають , зведений індекс цін — . Символи p та q не випадкові, вони відповідають початковим літерам англійських слів price (ціна) та quantity (кількість).

Індивідуальний індекс — це відносна величина динаміки

або порівняння

.

Неодмінною умовою їх обчислення є порівнянність методики вимірювання чисельника та знаменника відношення, що являє собою індекс.

Щодо зведених індексів, то розрахунок кожного з них окремо передбачає вирішення низки методологічних питань. У підрозд. 9.2 розглядається методологія побудови зведених індексів цін і товарної маси, які вважаються спряженими.

 

 

9.2. Методологічні основи побудови зведених індексів

 

Зведений індекс показує, як у середньому змінився показник по сукупності елементів. Основою побудови зведених індексів є агрегування, узагальнення інформації. Нехай за даними про ціни на товари (j = 1, 2, 3,...) за два періоди (t = 0,1) необхідно визначити зведений індекс цін:

та .

Агрегування інформації для зведеного індексу цін можна здійснити трьома способами.

1. У вигляді відношення сум цін (індекс Дюто, 1735 р.):

Поділивши чисельник і знаменник на n, цей індекс можна подати як відношення середніх цін.

2. Як середню арифметичну з індивідуальних індексів цін (індекс Карлі, 1751 р.):

.

3. Як середню геометричну з індивідуальних індексів (Джевон, 1863 р.):

.

Кожний з цих варіантів передбачає рівновагомість товарів у сукупності. Інакше зведений індекс неадекватно характеризуватиме сукупну зміну цін. Адже не можна визначити середню ціну, наприклад, 1 л вина та 1 кг хліба. Так само без урахування вагомості окремих товарів неможливо усереднити індивідуальні індекси цін: якщо ціни на хліб зросли на 10%, а на вино — удвічі, то це не означає, що в середньому ціни зросли на 55%.

Отже, при розрахунку зведеного індексу кожному j -му елементу необхідно надати певну «вагу», яка б ураховувала його відносну значущість. Очевидно, що ваги повинні мати однакову розмірність. Кількості товару q_j у натуральних одиницях вимірювання не можуть виконувати вагову функцію, а тому вагами є вартості товарів q_j p_j. Припустимо, що в базисному періоді вартості товарів становили q_{j 0} p_{j 0}, тоді зважений індекс цін набирає вигляду

Це дві форми одного індексу — середньозважена та агрегатна. Основою середньозваженої форми є індекс Карлі, агрегатної — індекс Дюто.

Аналогічна ситуація виникає при агрегуванні фізичного обсягу продукції (товарної маси, кількості), якщо елементи сукупності не сумірні між собою, тобто не мають спільної міри:

та .

У такому разі їх агрегування можливе лише за умови зведення різнорідних елементів до одного порівнянного виду за допомогою певних сумірників. Найчастіше сумірниками є вартісні показники — ціна або собівартість одиниці продукції. Наприклад, при визначенні обсягів проданих на біржі товарів — металу, лісоматеріалів, цементу — сумірниками виступають ціни. Обсяги продажу записуються як Якщо за сумірник узяти собівартість с, агрегат інтерпретується як грошові витрати і набирає вигляду

Іноді зручнішим є трудовий сумірник. Наприклад, при визначенні обсягів виконаних у сільському господарстві робіт (оранка, боронування, сівба тощо) як сумірник використовують трудомісткість, тобто затрати праці на одиницю виконаної роботи (позначимо t). Тоді загальний обсяг трудових затрат буде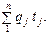

Зведений індекс фізичного обсягу також має дві форми — середньозважену та агрегатну:

Як бачимо з формул наведених індексів та , їх значення залежить від структури агрегату і динаміки окремих його елементів. Тому при визначенні зведеного індексу необхідно передусім обґрунтувати коло елементів, які підлягають агрегуванню в одне ціле. Наприклад, обґрунтовується споживчий кошик (набір споживчих товарів) при обчисленні індексу «вартості життя», перелік товарів і товарних груп при обчисленні індексу оптових цін тощо.

Підсумовування ведеться по всьому визначеному колу елементів як у чисельнику, так і в знаменнику, а тому надалі для простоти викладу навчального матеріалу у формулах зведених індексів ідентификаційні позначки елементів не вказуються.

 

9.3. Агрегатна форма індексів

 

Агрегатний індекс — це співвідношення двох агрегатів, конкретних щодо змісту й часу. Агрегат є добутком спряжених величин. Одна з цих величин індексована — у чисельнику і знаменнику вона в різних періодах, інша є вагою чи сумірником індексованої величини і фіксується на одному й тому самому рівні.

Так, в індексі цін індексується ціна p, а кількість q являє собою вагу ціни і фіксується на одному й тому самому рівні; в індексі фізичного обсягу продукції індексується кількість q, а сумірник кількості — ціна p — фіксується:

Ваги в індексі цін і сумірники в індексі фізичного обсягу можна фіксувати на рівні як базисного, так і поточного періоду. Для ілюстрації варіантів зважування використаємо матрицю агрегатів (рис. 9.1).

Рис. 9.1. Схема співвідношення агрегатів

На головній діагоналі матриці розміщено фактичні вартості товарів, на побічній — перехресні (умовні). По горизонталі розміщені агрегати з фіксованими вагами: у першому — на рівні базисного періоду, у другому — на рівні поточного. По вертикалі — агрегати з фіксованими сумірниками: у першому — на рівні базисного періоду, у другому — на рівні поточного. Порівняння агрегатів дає дві системи індексів — базисно-зважену (Ласпереса) та поточно-зважену (Пааше).

У базисно-зваженій системі перехресні агрегати побічної діагоналі порівнюються з базисним агрегатом головної діагоналі , у поточно-зваженій системі агрегат головної діагоналі порівнюється з перехресними агрегатами побічної діагоналі. Схематично системи зважування показано на рис. 9.1, а формули індексів наведені в табл. 9.1.

Таблиця 9.1

ФОРМУЛИ ІНДЕКСІВ ЦІН І ФІЗИЧНОГО ОБСЯГУ
ЗА РІЗНИХ СИСТЕМ ЗВАЖУВАННЯ

Базисно-зважена система (Ласпереса)	Поточно-зважена система (Пааше)

 

Обидві системи індексів рівноправні. Реальний економічний зміст мають не лише чисельник і знаменник індексу, а й різниця між ними. Вибір форми індексу залежить від мети дослідження та наявної інформації. Так, у зарубіжній статистиці індекс цін розраховується за Ласпересом, оскільки ґрунтується на даних про обсяги, отримані з переписів, вибіркових обстежень домогосподарств, інших джерел за минулий період. У вітчизняній статистиці при розрахунках індексів цін перевага надавалася формулі Пааше, оскільки визначальним показником була вартість поточного періоду. Індекс фізичного обсягу товарної маси, навпаки, обчислюється за формулою Ласпереса з фіксованими сумірниками на рівні базисного періоду. У такому разі динаміка цінового фактора не впливає на величину індексу. Зауважимо, що при незначній кореляції між цінами та товарною масою індекси, розраховані за Ласпересом і Пааше, практично однакові.

Розглянемо порядок розрахунку агрегатних індексів за даними про ціни та обсяги продажу через біржу агропродукції (табл. 9.2). У цьому прикладі агрегатами виступають фактичні за кожний місяць та умовні обсяги торгових оборотів біржи.

Таблиця 9.2

ДО РОЗРАХУНКУ АГРЕГАТНИХ ІНДЕКСІВ ЦІН І ФІЗИЧНОГО ОБСЯГУ

Продукція	Реалізовано, тис. т	Ціна за 1 т, грн.	Агрегати (торгові обороти, тис. грн.)
Серпень	Вересень	Серпень	Вересень	q 0 p 0	q 1 p 0	q 1 p 1	q 0 p 1
q 0	q 1	p 0	p 1
Борошно
Цукор
Олія
Разом	´	´	´	´

 

За даними таблиці зведені індекси цін та фізичного обсягу , реалізованої через біржу агропродукції, становлять:

 

За Ласпересом:	За Пааше:

 

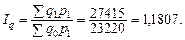
Тобто, біржові ціни на агропродукцію у вересні порівняно із серпнем зменшилися в середньому на 1,4%, реалізована товарна маса зросла в середньому на 18%.

Оскільки в структурі торгового обороту не відбулося значних змін, то розбіжності між індексами, обчисленими за різними системами зважування, неістотні. Будь-який з розрахованих індексів має певний ступінь умовності.

За наявності структурних зрушень у торгових оборотах використовують індекси із середніми вагами або усереднення різнозважених індексів за допомогою середньої геометричної, наприклад, індекс цін

.

Спираючись на формально-математичні критерії, яким відповідає усереднений індекс, І. Фішер назвав його «ідеальним», проте через відсутність конкретного економічного змісту цей індекс не набув широкого практичного застосування.

9.4. Середньозважені індекси

 

Другою формою зведеного індексу є середньозважений з індивідуальних індексів. Використовують два види середніх — арифметичну та гармонічну. Вибір виду середньої ґрунтується на загальних засадах: середньозважений індекс має бути тотожним відповідному індексу агрегатної форми.

Подамо інформацію про біржові торги агропродукцією обсягами торговельного обороту (у серпні — , у вересні — ) та індивідуальними індексами цін і фізичного обсягу продажу (табл. 9.3).

Таблиця 9.3

ДО РОЗРАХУНКУ СЕРЕДНЬОЗВАЖЕНИХ ІНДЕКСІВ
ЦІН І ФІЗИЧНОГО ОБСЯГУ

Товар	Торговельний оборот, тис. грн.	Індивідуальні індекси	Умовний агрегат
Серпень	Вересень	цін	фізичного обсягу	iq q 0 p 0
q 0 p 0	q 1 p 1	ір	іq
Борошно			0,9808	1,2500
Цукор			1,0143	1,1667
Олія			0,9600	1,1429
Разом			´	´

Умовний торговий оборот 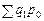можна визначити, скоригувавши фактичні обороти індивідуальними індексами цін або фізичного обсягу продажу:

У такому разі зведені індекси за Ласпересом обчислюються як середня арифметична з вагами 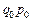, а індекси за Пааше — як середня гармонічна з вагами

	.

Обчислимо середньозважені індекси цін та фізичного обсягу продажу за даними табл. 9.3, використовуючи різні варіанти зважування ( — за Пааше, — за Ласпересом):

середньозважений індекс цін

середньозважений індекс фізичного обсягу продажу

.

Як бачимо, значення середньозважених індексів такі самі, як і відповідних їм агрегатних (див. підрозд. 9.3).

При побудові середньозважених індексів вартісні ваги можна замінити відносними величинами структури d, сума яких У цьому разі середньозважені індекси набирають вигляду

;

Ці формули підтверджують залежність значення зведеного індексу від динаміки окремих складових і пропорцій у сукупності агрегованих елементів.

Наприклад, у регіоні виробництво споживчих товарів зменшилось: продовольчих — на 3, непродовольчих — на 7%, а ціни зросли відповідно на 4 і 6%. Унаслідок нерівномірності динаміки виробництва по групах споживчих товарів змінилась їх структура: на 2 п. п. зросла частка продовольчих товарів і на стільки ж зменшилась частка непродовольчих. Розрахунки зведених індексів фізичного обсягу та цін наведено в табл. 9.4.

 

Таблиця 9.4

ДО РОЗРАХУНКУ СЕРЕДНЬОЗВАЖЕНИХ ІНДЕКСІВ
З ВІДНОСНИМИ ВАГАМИ

Товарні групи	Структура виробництва	Індивідуальні індекси	Розрахункові величини
d 0	d 1	іq	ір	іq d 0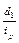
Продовольчі	0,60	0,62	0,97	1,04	0,582	0,596
Непродовольчі	0,40	0,38	0,93	1,06	0,372	0,358
Разом	1,00	1,00	´	´	0,954	0,954

Зведений індекс фізичного обсягу виробництва I_q = 0,97 × 0,60 + + 0,93 × 0,40 = 0,954 тобто в середньому обсяги виробництва зменшилися на 4,6%.

Зведений індекс цін 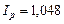показує, що ціни в середньому зросли на 4,8%:

.

Середньозважені індекси мають перевагу перед агрегатними, адже за їхньою допомогою можна вишикувати ієрархію індексів від індивідуальних на окремі товари через групові (субіндекси) до загального по всій сукупності елементів. Проте їм властиві й недоліки. Якщо динаміка окремих складових сукупності протилежна, то зведений індекс не в змозі адекватно відобразити закономірність динаміки. Окрім того, середньозважений індекс визначається лише стосовно порівнянного кола елементів. Якщо ж окремі елементи сукупності відсутні в базисному чи поточному періоді, то розрахунок індивідуальних індексів неможливий. У цьому разі перевага надається індексу агрегатної форми.

Отже, за кожним індексом стоїть певне економічне явище, що зумовлює методику його розрахунку та змістовність.

 

 

9.5. Взаємозв’язки індексів

 

Розглянуті зведені індекси узагальнюють динаміку складних
сукупностей. Не менш важливою в статистичному аналізі є друга функція індексів — аналітична, яка спирається на взаємозв’язок індексів. Практично кожний індекс є складовою певної індексної системи, а його зв’язки з іншими індексами цієї системи відбивають зв’язки між відповідними показниками. Так, товароборот залежить від фізичного обсягу проданого товару і цін , відповідно індекс товарообороту 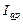можна подати як добуток індексів фізичного обсягу і цін:

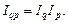
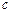Аналогічно грошові витрати на виробництво можна подати як функцію фізичного обсягу виробництва і собівартості , отже, обсяг виробництва — як функцію трудових затрат q та продуктивності праці , тобто і т. ін.

Отже, у будь-якій системі індекс добутку спряжених величин дорівнює добутку індексів цих величин. У рамках такої індексної системи на основі двох індексів можна визначити третій. Наприклад, якщо грошові витрати на виробництво зросли на 7,1%, а фізичний обсяг виробленої продукції — на 5%, то собівартість одиниці продукції зросла в середньому на 2%:

Взаємопов’язані також індекси прямих і обернених показників, наприклад, споживчих цін і купівельної спроможності грошової одиниці, продуктивності праці й трудомісткості продукції тощо. Якщо споживчі ціни зросли на 4,8%, то купівельна спроможність грошової одиниці зменшилася на 4,6%:

Показники-співмножники індексної системи є факторами показника-результату, а динаміка їх визначає динаміку останнього. Отже, у межах індексної системи можна визначити роль кожного окремого фактора, оцінити його вплив на динаміку результату. Така оцінка ґрунтується на методі абстракції. Аби виявити вплив одного фактора, необхідно абстрагуватись від впливу іншого, зафіксувати його на постійному рівні. Проте постає питання: на
рівні якого періоду — базисного чи поточного? Теоретично можливі два варіанти.

Перший: коли обидва індекси-співмножники базисно-зважені, кожний з них оцінює окремий вплив, оцінки впливу порівнянні. Проте цей варіант не забезпечує пов’язування індексів у систему:

У другому варіанті індекси-співмножники різнозважені: ваги одного з них фіксуються на рівні базисного періоду, іншого — на рівні поточного. Через різнозваженість індексів оцінки впливу факторів непорівнянні, але саме такий порядок абстрагування впливу факторів забезпечує взаємозв’язок індексної системи:

або

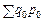У розглянутому прикладі (див. табл. 9.2) результативний показник індексної системи — біржовий оборот. Його індекс обчислюється як відношення фактичних вартостей поточного періоду = 27415 і базисного = 23550:

,

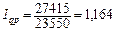тобто біржовий оборот зріс на 16,4%. Цей індекс можна записати як добуток індексів фізичного обсягу продажу і цін

1,164 = 1,181 × 0,986.

Отже, зведені індекси цін і товарної маси , маючи самостійне значення, водночас виконують аналітичну функцію — оцінюють вплив відповідного фактора на динаміку біржового обороту. Ступінь впливу факторів на результат характеризують темпи приросту факторів. У розглянутому прикладі за рахунок збільшення товарної маси біржовий оборот зріс на 18%, зниження цін призвело до зменшення біржового обороту на 1,4%.

У межах індексної системи можна визначити також абсолютний вплив факторів на приріст результату. Абсолютний приріст біржового обороту

У нашому прикладі

= 27415 – 23550 = 3865 тис. грн.

Він спричинений обома факторами, тобто товарною масою і цінами :

Абсолютний вплив кожного фактора окремо визначається як різниця між чисельником і знаменником відповідного індексу:

,

.

Згідно з даними табл. 9.2, тис. грн.:

,

27415 – 27800 = – 385.

Разом: 3865.

Якщо абсолютний вплив факторів односпрямований, можна визначити питому вагу кожного фактора. При різноспрямованих впливах такі розрахунки не мають сенсу.

Коли факторів три і більше, передусім необхідно визначити їх послідовність, ураховуючи суть кожного з них, порядок розрахунку, взаємозв’язок у системі. Наприклад, y = abc. Припустимо, що результативний показник у — відносна величина. Тоді першим фактором-співмножником буде той, чисельник розрахункової формули якого є чисельником результативного показника; у наступного фактора-співмножника чисельник розрахункової фор­мули є знаменником першого фактора і т. д.

Наприклад, y — прибутковість власного капіталу фірми, a — при­бутковість поточних активів, b — коефіцієнт поточної ліквідності, c — частка поточних пасивів у власному капіталі. Згідно з розрахунковими формулами послідовність факторів у системі така:

Отже, Ваги в індексах-співмножниках фіксуються за схемою: в індексі першого фактора — на рівні базисного періоду, в індексі другого фактора — ті, що праворуч від індексованої величини, на рівні базисного періоду, ті, що ліворуч, — на рівні поточного періоду, в індексі третього фактора — усі ваги фіксуються на рівні поточного періоду (вони розміщені ліворуч від індексованої величини).

У символах система зважування факторів має такий вигляд:

.

Як і у двофакторній індексній системі, абсолютний вплив зміни будь-якого фактора на динаміку результату визначається як різниця між чисельником і знаменником відповідного індексу. Тотожні оцінки абсолютного впливу факторів дає ланцюговий метод, який ґрунтується на умовних значеннях результативного показника. Замінимо Тоді — значення результативного показника за умови, що на динаміку останнього впливає лише фактор . Різниця характеризує абсолютний приріст за рахунок фактора . Аналогічно визначається абсолютний вплив інших факторів:

Очевидно, що

Наприклад, прибутковість власного капіталу зменшилась з 32% у базисному періоді до 24% у поточному, тобто на 8 п. п. Індекс прибутковості становить І_у = 24: 32 = 0,75. За той же період прибутковість активів зменшилась на 10%, поточна ліквідність — на 15%, частка поточних пасивів у власному капіталі — на 2%.

Індексна система має вигляд:

0,90 · 0,85 · 0,98 = 0,75.

Розрахунок абсолютного впливу факторів на динаміку прибутковості капіталу подано в табл. 9.5.

Таблиця 9.5

АБСОЛЮТНИЙ ВПЛИВ ФАКТОРІВ НА ЗМЕНШЕННЯ
ПРИБУТКОВОСТІ ВЛАСНОГО КАПІТАЛУ

Фактор	Індекс	Розрахункова величина	Абсолютний вплив фактора, п.п.
а	0,90	32,0 · 0,90 = 28,8	28,8 – 32,0 = –3,2
b	0,85	28,8 · 0,85 = 24,5	24,5 – 28,8 = –4,3
с	0,98	24,5 · 0,98 = 24,0	24,0 – 24,5 = –0,5
Разом	´	´	–8,0

 

За даними таблиці найвагоміший вплив на зменшення прибутковості капіталу виявив фактор b — поточна ліквідність.

 

9.6. Індекси середніх величин

 

Поряд зі зведеними, агрегатними індексами в статистичній практиці широко використовують індекси середніх величин (індекси середньої заробітної плати, середньої врожайності тощо). Як відомо, рівень середньої залежить від значень ознаки х_j і структури сукупності:

де f_j — частота; d_j — частка j- ї складової сукупності.

Очевидно, що й динаміка середньої визначається цими факторами: а) зміною значень ознаки x_j і б) структурними зрушеннями. Вплив кожного з них на динаміку середньої оцінюється за допомогою системи індексів середніх величин: змінного й фіксованого складу, а також структурних зрушень. У наведених формулах індексів ідентифікація складових сукупності відсутня.

Індексом змінного складу називають індекс середньоївеличини, він відбиває не лише зміни значень ознаки х, а й зміни в структурі сукупності:

.

В індексі фіксованого складу ваги постійні, тобто усувається вплив на динаміку середньої структурних зрушень. Величина показує, як у середньому змінилися значення ознаки при незмінній, фіксованій структурі:

Індекс структурних зрушень I_d, навпаки, показує, як змінилася середня за рахунок структурних зрушень; значення ознаки x фіксуються на постійному рівні:

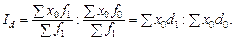
У кожній конкретній індексній системі I_d оцінює вплив на динаміку середньої того структурного фактора, який є основою поділу сукупності на складові.

Формули індексів фіксованого складу і структурних зрушень різнозважені: в I_x ваги фіксуються на рівні поточного періоду, в I_d — значення ознаки x — на рівні базисного періоду. Саме такий варіант зважування забезпечує пов’язування цих індексів у систему:

Розглянемо побудову індексів середніх величин на прикладі трудомісткості продукції одного виду, яка виготовляється за різними технологіями (табл. 9.6).

Таблиця 9.6

ДО РОЗРАХУНКУ ІНДЕКСІВ СЕРЕДНІХ ВЕЛИЧИН

Технологія	Виробництво продукції, шт.	Затрати праці на один виріб, людино-год	ix	Розрахункові величини
Базисний пріод f 0	Поточний період f 1	Базисний період x 0	Поточний період x 1	x 0 f 0	x 0 f 1	x 1 f 1
А			2,0	1,8	0,900
Б			2,8	2,5	0,893
Разом			´	´	´

За поточний період затрати праці на виготовлення одного виробу зменшилися: за технологією А — на 10% ( = 0,900), за технологією Б — на 10,7% (i_x = 0,893). Водночас змінилася структура виробництва: на 20 п. п. зросла частка виробництва за менш трудомісткою технологією А, на стільки ж пунктів зменшилася частка виробництва за технологією Б. Середні затрати праці на один виріб у базисному періоді людино-год, у поточному людино-год, тобто змен­шилися на 16,4%:

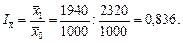
Індекс змінного складу значно менший за індивідуальні індекси затрат праці. Такий парадоксальний результат пояснюється тим, що на динаміку середньої вплинула не лише динаміка трудомісткості виробу по окремих технологіях, а й структурні зрушення в обсягах виробництва.

Зафіксувавши структуру виробництва на одному й тому самому рівні (поточному), визначимо, як у середньому змінилася трудомісткість продукції. Індекс фіксованого складу

тобто в середньому затрати праці на виробництво одного виробу зменшилися на 10,2%.

Індекс фіксованого складу I_x тотожний середньозваженому гармонічному індексу з індивідуальних індексів затрат праці з поточними вагами:

За рахунок структурних зрушень, а саме збільшення обсягів виробництва за менш трудомістською технологією А, середня трудомісткість виробництва зменшилася на 6,9%:

Система індексів середніх величин має вигляд:

.

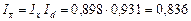У рамках індексної системи можна визначити абсолютні прирости середньої за рахунок кожного фактора: =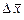
= 1,94 – 2,32 = – 0,38 людино-год, у тому числі за рахунок трудомісткості окремих технологій = 1,94 – 2,16 = – 0,22, за рахунок структурних зрушень = 2,16 – 2,32 = – 0,16.

Методологічною особливістю побудови системи індексів середніх величин є порівнянність складових сукупності в часі. Проте більшість реальних сукупностей за своїм складом динаміч­ні: одні частини сукупності зникають, інші (нові) — з’являються. Так, оновлюється асортимент продукції, на ринку цінних паперів з’яв­ляються нові емітенти, у видобувній промисловості вводяться в експлуатацію нові родовища і т. ін.

Щоб оцінити вплив на динаміку середньої такого роду змін, в індексну систему вводять три індекси структурних зрушень: — для оцінювання впливу змін у структурі порівнянного кола складових сукупності; — для оцінювання впливу новоутворених складових, 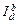— для оцінювання впливу вибулих складових. Індексна система має вигляд

.

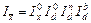Індекс фіксованого складу 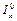обчислюється для порівнянного кола складових. Вагами всіх індексів є відносні величини структури — частки .

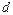Отже,

;

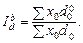
Наприклад, на ринку пального діють чотири постачальники високооктанового автобензину: A, B, C, D. У березні постачальниками A, B, C поставлено 250 тис. т бензину, у квітні постачальниками A, B, D — 300 тис. т. Ціни на автобензин у постачальників різні (табл. 9.7). Середня ціна 1 тонни автобензину в березні становила = 324,5 грн., у квітні — = 314,6, що на 3% менше:

= = 314,6: 324,5 = 0,970.

Постійними на ринку були постачальники A і B. У квітні вони знизили ціну на автобензин у середньому на 2,1%, індекс фіксованого складу

Таблиця 9.7

ДО РОЗРАХУНКУ СИСТЕМИ ІНДЕКСІВ СТРУКТУРНИХ ЗРУШЕНЬ

Постачальники	Ціна 1 т, грн.	Обсяг поставок, тис.т	Частка поставки
Березень	Квітень	Березень	Квітень	у загальному обсязі	по порівнянному колу
х 0	х 1	f 0	f 1	d 0	d 1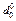
А					0,48	0,47	0,60	0,70
В					0,32	0,20	0,40	0,30
С		—		—	0,20	—	—	—
D	—		—		—	0,33	—	—
Разом	´	´			1,0	1,0	1,0	1,0

 

За рахунок структурних зрушень в обсягах поставки постійних постачальників середня ціна автобензину зменшилася на 0,2%:

.

Вихід з ринку автобензину постачальника C з відносно низькою ціною призвів до збільшення середньої ціни на 0,6%:

.

Поява на ринку нового постачальника D з найнижчою ціною спричинила зниження середньої ціни на 1,3%:

Очевидний взаємозв’язок індексів

Отже, динаміка середньої ціни на автобензин формувалася за рахунок як динаміки цін в окремих постачальників, так і різно-
спрямованої дії структурних факторів.

 

 

Територіальні індекси

 

Територіальний індекс використовують як інструмент порівняння соціально-економічних показників у просторі: за окремими країнами, територіями, регіонами, об’єктами. Особливістю цих індексів є рівноправність порівнюваних об’єктів А і В. Жоден з них не може претендувати на роль бази порівняння, а отже рівноправними слід вважати індекси як з базою порівняння А, так і з базою порівняння В:

; .

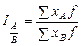Де х — індексована величина, f — вага (сумірник) індексованої величини.

При фіксованих значеннях ваг (сумірників) індекси і обернено пропорційні. Так, використовуючи світові ціни, можна привести до порівняльного виду обсяги експорту окремих країн, регіонів, спільних підприємств. Якщо, скажімо, екпорт об’єкта А перевищує екcпорт об’єкта В на 15% , то експорт об’єкта В менший за експорт об’єкта А на 13% . Вибір бази порівняння підпорядковується меті дослідження.

Значно складнішим є вибір варіанта зважування. Якщо товарна структура експорту за об’єктами різниться, то результати порівняння будуть неоднозначні, про що свідчать індекси, розраховані за умовними даними табл. 9.8.

Таблиця 9.8.