Оцінка щільності та перевірка істотності кореляційного зв’язку

Поряд із визначенням характеру зв’язку та ефектів впливу факторів х на результат у важливе значення має оцінка щільності зв’язку, тобто оцінка узгодженості варіації взаємозв’язаних ознак. Якщо вплив факторної ознаки х на результативну у значний, це виявиться в закономірній зміні значень у зі зміною значень х, тобто фактор х своїм впливом формує варіацію у. За відсутності зв’язку варіація у не залежить від варіації х.

Для оцінювання щільності зв’язку статистика використовує низку коефіцієнтів з такими спільними властивостями:

· за відсутності будь-якого зв’язку значення коефіцієнта наближається до нуля; при функціональному зв’язку — до одиниці;

· за наявності кореляційного зв’язку коефіцієнт виражається дробом, який за абсолютною величиною тим більший, чим щільніший зв’язок.

Серед мір щільності зв’язку найпоширенішим є коефіцієнт кореляції Пірсона. Позначається цей коефіцієнт символом r. Оскільки сфера його використання обмежується лінійною залежністю, то і в назві фігурує слово «лінійний». Обчислення лінійного коефіцієнта кореляції r ґрунтується
на відхиленнях значень взаємозв’язаних ознак x і у від середніх.

За наявності прямого кореляційного зв’язку будь-якому значенню х_і > відповідає значення , а 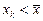відповідає . Узгодженість варіації х і у схематично показано на рис. 7.2 у вигляді кореляційного поля зі зміщеною системою координат.

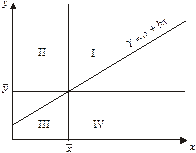
Рис. 7.2. Узгодженість варіації взаємозв’язаних ознак

 

Точка, координатами якої є середні і , поділяє кореляційне поле на чотири квадранти, в яких по-різному поєднуються знаки відхилень від середніх:

 

Квадрант	(х – )	(у – )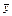
I	+	+
II	–	+
III	–	–
IV	+	–

 

Для точок, розміщених у І та ІІІ квадрантах, добуток додатний, а для точок з квадрантів ІІ і ІV — від’ємний. Чим щільніший зв’язок між ознаками х і у, тим більша алгебраїчна сума добутків відхилень . Гранична сума цих добутків дорівнює .

Коефіцієнт кореляції визначається відношенням зазначе-
них сум:

.

Очевидно, що в разі функціонального зв’язку фактична сума відхилень дорівнює граничній, а коефіцієнт кореляції r = ±1; при кореляційному зв’язку абсолютне його значення буде тим більшим, чим щільніший зв’язок.

На практиці застосовують різні модифікації наведеної формули коефіцієнта кореляції. Для оцінювання щільності зв’язку між кількістю внесених добрив та врожайністю зернових скористаємося однією з модифікацій зазначеної формули:

.

За даними табл. 7.3

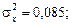
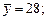
Згідно з цими значеннями коефіцієнт кореляції становить 0,900, що свідчить про вагомий вплив кількості внесених добрив на врожайність зернових:

.

Коефіцієнт кореляції, оцінюючи щільність зв’язку, указує також на його напрям: коли зв’язок прямий, r — величина додатна, а коли він зворотний — від’ємна. Знаки коефіцієнтів кореляції і регресії однакові, величини їх взаємозв’язані функціонально:

; .

Завдяки цьому один коефіцієнт можна обчислити, знаючи інший. Наприклад:

.

Вимірювання щільності нелінійного зв’язку ґрунтується на співвідношенні варіацій теоретичних та емпіричних (фактичних) значень результативної ознаки у. Як зазначалося в підрозд. 5.6, відхилення індивідуального значення ознаки у від середньої 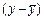можна розкласти на дві складові. У регресійному аналізі це відхилення від лінії регресії (у – Y) та відхилення лінії регресії від середньої .

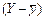Відхилення є наслідком дії фактора х, відхилення — наслідком дії інших факторів. Взаємозв’язок факторної та залишкової варіацій описується правилом декомпозиції варіації:

,

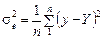де — загальна дисперсія ознаки y; — факторна дисперсія; — залишкова дисперсія.

Очевидно, значення факторної дисперсії буде тим більшим, чим сильніший вплив фактора х на y. Відношення факторної дисперсії до загальної розглядається як міра щільності кореляційного зв’язку і називається коефіцієнтом детермінації:

.

Якщо за даними табл. 7.3 , , то .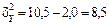

Аналогічний результат дають такі обчислення:

.

Коефіцієнт детермінації становить ,

тобто 81% варіації врожайності зернових залежить від варіації кількості внесених добрив, а 19% припадає на інші фактори.

Корінь квадратний з коефіцієнта детермінації називають індексом кореляції R. Коли зв’язок лінійний, , що підтверджують обчислення: Тому за відомим лінійним коефіцієнтом кореляції r можна визначати внесок ознаки x у варіацію ознаки y. Так, при r = 0,6 можна сказати, що 36% варіації y залежить від варіації x.

На таких самих засадах ґрунтується оцінювання щільності зв’язку за даними аналітичного групування. Мірою щільності зв’язку є кореляційне відношення

,

де d² — міжгрупова дисперсія, яка вимірює варіацію ознаки у під впливом фактора х, а s² — загальна дисперсія.

Застосуємо кореляційне відношення для оцінювання щільності зв’язку між глибиною розробки вугільних пластів і фондомісткістю видобутку вугілля (див. табл. 7.2). Розрахунки загальної та факторної дисперсій подано в табл. 7.4 та 7.5. Згідно з розрахунками загальна дисперсія становить 5,19, факторна — 3,86:

;

.

Кореляційне відношення

,

тобто 74,5% варіації фондомісткості вугілля на шахтах регіону пояснюється варіацією глибини розробки пластів.

Таблиця 7.4

ДО РОЗРАХУНКУ ЗАГАЛЬНОЇ ДИСПЕРСІЇ
ФОНДОМІСТКОСТІ ВУГІЛЛЯ ()

Фондомісткість, грн. / т	18—20	0—22	22—24	24—26	26—28	Разом
Кількість шахт
						´
	– 4,5	–2,5	–0,5	1,5	3,5	´
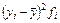
	182,25	93,75	8,5	63,0	171,5

Таблиця 7.5

ДО РОЗРАХУНКУ ФАКТОРНОЇ ДИСПЕРСІЇ
ФОНДОМІСТКОСТІ ВУГІЛЛЯ ()

Глибина розробки пластів, м
До 300		20,0	–3,5	208,25
300 — 500		22,9	–0,6	14,40
500 — 700		24,8	1,3	42,25
700 і більше		26,1	2,6	121,68
У цілому		23,5	´	386,58

Обчислення та інтерпретація коефіцієнта детермінації R ² і кореляційного відношення h² показують: ці характеристики щільності зв’язку за змістом ідентичні, вони характеризують внесок фактора x у загальну варіацію результату y.

Перевірка істотності кореляційного зв’язку ґрунтується на порівнянні фактичних значень R ² і h² з критичними, які могли б виникнути за відсутності зв’язку. Якщо фактичне значення чи h² перевищує критичне, то зв’язок між ознаками не випадковий. Гіпотеза, що перевіряється, формулюється як нульова:

або .

Критичні значення характеристик щільності зв’язку для рівня істотності a = 0,05 і відповідного числа ступенів свободи для факторної дисперсії k ₁ і залишкової k ₂ наведено в табл. 7.6. Ступені свободи залежать від обсягу сукупності n та числа груп або параметрів функції m, тобто k ₁ = m – 1, k ₂ = n – m.

 

 

 

Таблиця 7.6

КРИТИЧНІ ЗНАЧЕННЯ КОЕФІЦІЄНТА ДЕТЕРМІНАЦІЇ R²
І КОРЕЛЯЦІЙНОГО ВІДНОШЕННЯ h² ДЛЯ РІВНЯ ІСТОТНОСТІ a = 0,05

	0,569

Так, критичне значення коефіцієнта детермінації для k ₁ = 2 – 1 = 1 і k ₂ = 8 – 2 = 6 становить . Обчислений за даними табл. 7.3 коефіцієнт детермінації R ² = 0,81 перевищує критичне значення, що з імовірністю 0,95 підтверджує істотність зв’язку між кількістю внесених добрив і врожайністю зернових.

Аналогічно визначимо критичне значення кореляційного відношення для k ₁ = 4 – 1 = 3 та k ₂ = 100 – 4 = 96. Оскільки значення k ₂ = 96 у табл. 7.6 відсутнє, можна використати найближче до нього число k ₂ = 100. Критичне значення .

Розраховане за даними табл. 7.2 кореляційне відношення h² = 0,745 значно перевищує критичне, а отже, гіпотеза про випадковий характер відхилень групових середніх відхиляється. Зв’язок між глибиною розробки вугільних пластів і фондомісткістю видобутку вугілля з імовірністю 0,95 визнається істотним.

Розглянута процедура перевірки істотності зв’язку є складовою дисперсійного аналізу, розробленого Р. Фішером. Характеристика критерію Фішера — дисперсійне відношення F — функціонально пов’язана з кореляційним відношенням , а тому результати перевірки будуть ідентичні.

6.4. Рангова кореляція

 

Взаємозв’язок між ознаками, які можна зранжувати, передусім на основі бальних оцінок, вимірюється методами рангової кореляції. Рангами називають числа натурального ряду, які згідно зі значеннями ознаки надаються елементам сукупності і певним чином упорядковують її. Ранжування проводиться за кожною ознакою окремо: перший ранг надається найменшому значенню ознаки, останній — найбільшому або навпаки. Кількість рангів дорівнює обсягу сукупності. Очевидно, зі збільшенням обсягу сукупності ступінь «розпізнаваності» елементів зменшується. З огляду на те, що рангова кореляція не потребує додержання будь-яких математичних передумов щодо розподілу ознак, зокрема вимоги нормальності розподілу, рангові оцінки щільності зв’язку доцільно використовувати для сукупностей невеликого обсягу.

Ранги, надані елементам сукупності за ознаками х і у, позначають відповідно Rx_j та Ry_j. Залежно від ступеня зв’язку між ознаками певним чином співвідносяться й ранги. При прямому функціональному зв’язку Rx_j = Ry_j, тобто відхилення між рангами d_j = Rx_j – Ry_j = 0, отже, і сума квадратів відхилень . При зворотному функціональному зв’язку де n —
число рангів. Якщо зв’язок між ознаками відсутній, 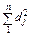являє собою середню арифметичну цих крайніх значень:

,

а отже,

.

Спираючись на зазначену математичну тотожність, К. Спір­мен запропонував формулу для коефіцієнта рангової кореляції:

.

Цей коефіцієнт має такі самі властивості, як і лінійний коефіцієнт кореляції: змінюється в межах від – 1 до + 1, водночас оцінює щільність зв’язку та вказує на його напрям.

Визначимо коефіцієнт рангової кореляції за даними експертних оцінок ефективності економіки та ступеня політичного ризику для семи країн з перехідною економікою (табл. 7.7). Оскільки експертні оцінки представлені балами, необхідно провести ранжування країн. За оцінками ефективності економіки країні з найбільшим балом надається ранг 1, з найменшим — ранг n = 7. За оцінками ступеня політичного ризику, навпаки, ранг 1 надається країні з найменшим ризиком, а ранг 7 — країні з найбільшим ризиком.

Таблиця 7.7

ДО РОЗРАХУНКУ КОЕФІЦІЄНТА РАНГОВОЇ КОРЕЛЯЦІЇ

№ з/п	Експертні оцінки, балів	Ранги	dj = Rxj – Ryj
Ефективність економіки (mах= 10)	Ступінь політичного ризику (mах = 100)	Rxj	Ryj
	6,6	64,5			–6
	5,8	57,8			–4
	2,9	23,6
	3,4	36,2
	4,5	45,3			–2
	2,7	28,4
	4,2	32,7
Разом	´	´	´	´	´

Сума квадратів відхилень рангів , а коефіцієнт рангової кореляції

.

Значення коефіцієнта рангової кореляції свідчить про наявність зворотного і досить високого рівня зв’язку між ефективністю економіки і ступенем політичного ризику. Критичне значення коефіцієнта рангової кореляції (табл. 7.8) для рівня істотності a = 0,05 і n = 7 Отже, з імовірністю 0,95 істотність зв’язку доведено.

Таблиця 7.8

КРИТИЧНІ ЗНАЧЕННЯ КОЕФІЦІЄНТА
РАНГОВОЇ КОРЕЛЯЦІЇ СПІРМЕНА ПРИ 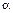= 0,05

Обсяг вибірки n
	0,90	0,83	0,71	0,64	0,60	0,56	0,53	0,50

 

Якщо два і більше елементів сукупності мають однакові значення ознаки, їм надається середній ранг. Нехай, наприклад, друге за розміром значення ознаки мають три елементи сукупності (№ 2, 3, 4), тоді всім їм надається ранг а щільність зв’язку можна оцінити за формулою лінійного коефіцієнта кореляції.

 

6.5. Оцінка узгодженості варіації атрибутивних ознак

 

Взаємозв’язки між атрибутивними ознаками аналізуються на підставі таблиць взаємної спряженості (співзалежності). Як приклад розглянемо табл. 7.9, в якій наведено результати соціологічного опитування населення щодо намірів прилучитися до ринку цінних паперів. Тих, хто не боїться ризикувати, класифікували як ризикованих інвесторів, тих, хто не уявляє ризику без гарантій, — обережними, а хто ризику уникає взагалі, — неризикованими.

Частоти комбінаційного розподілу респондентів за віком і схильністю до ризику концентруються навколо діагоналі з верхнього лівого кута в нижній правий. Серед молодих більшість готова ризикувати на ринку цінних паперів, у середній віковій групі готовий ризикувати один з п’яти, а половина не уявляє ризику без гарантій, у третій віковій групі на одного обережного припадають два неризиковані.

Таблиця 7.9

РОЗПОДІЛ РЕСПОНДЕНТІВ ЗА ВІКОМ І СХИЛЬНІСТЮ ДО РИЗИКУ

Вік х, років	Тип інвестора у	Разом fi 0
Ризикований	Обережний	Неризикований
16—30
31—50
51 і більше
Разом f 0 j

 

Характер розподілу частот, концентрація їх уздовж головної діагоналі свідчать про наявність стохастичного зв’язку між віком і схильністю до ризику.

Оцінка щільності стохастичного зв’язку ґрунтується на відхиленнях частот (часток) умовного та безумовного розподілів, тобто на відхиленнях фактичних частот f_ij від теоретичних F_ij, пропорційних до підсумкових:

,

де f_{i 0} — підсумкові частоти за ознакою x; f _{0 j} — підсумкові частоти за ознакою ; 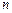— обсяг сукупності .

Якби схильність до ризику не залежала від віку, то кількість ризикованих серед молоді становила б

,

обережних у другій віковій групі

,

неризикованих у третій віковій групі

.

Абсолютну величину відхилень фактичних частот f_ij від пропорційних F_ij характеризує квадратична спряженість c² Пірсона:

.

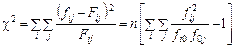За відсутності стохастичного зв’язку c² = 0. На основі розподілу ймовірностей c² перевіряється істотність зв’язку. Критичні значення c² для a = 0,05 і числа ступенів свободи k = (m_x – 1)
(m_y – 1) наведено в табл. 7.10. Так, для k = (3 – 1) (3 – 1) = 4 критичне значення Фактичне значення

що значно перевищує критичне, а отже, з імовірністю 0,95 істотність зв’язку між віком і схильністю до ризику доведено.

Відносною мірою щільності стохастичного зв’язку слугує коефіцієнт взаємної спряженості (співзалежності). За умови, що m_x = m_y використовують формулу Чупрова:

,

де m_x — число груп за ознакою x; m_y — число груп за ознакою y. Оскільки за відсутності зв’язку між ознаками c² = 0, то і С = 0. При функціональному зв’язку C ® 1. У разі, коли m_x ¹ m_x, віддають перевагу коефіцієнту спряженості Крамера:

,

де m _min — мінімальне число груп (m_x або m_y).

У нашому прикладі m_x = m_y = 3, а тому наведені формули коефіцієнта взаємної спряженості тотожні:

,

що свідчить про наявність зв’язку.

Таблиця 7.10

КРИТИЧНІ ЗНАЧЕННЯ

k
	3,84	5,99	7,81	9,49	11,07	12,59	14,07	15,51

 

Якщо обидві взаємозв’язані ознаки альтернативні, тобто кількість груп m_x = m_y = 2, то за відсутності зв’язку добутки діагональних частот однакові: f ₁₁ f ₂₂ = f ₁₂ f ₂₁. Саме на відхиленнях добут­ків частот ґрунтуються характеристики зв’язку:

,

.

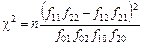У літературі зі статистики коефіцієнт для 4-клітинкової таблиці називається коефіцієнтом контингенції або асоціації. Очевидно, що за змістом він ідентичний коефіцієнту взаємної спряженості, а з c² пов’язаний функціонально: c² = nC ².

За допомогою коефіцієнта контингенції оцінимо щільність зв’язку між шкідливою звичкою палити і хворобами легенів (табл. 7.11).

Таблиця 7.11

РОЗПОДІЛ ПАЦІЄНТІВ КЛІНІКИ ЗА РЕЗУЛЬТАТАМИ ЛЕГЕНЕВИХ ПРОБ

Наявність звички палити	Результати легеневих проб	Разом
Аномальні	Нормальні
Палить
Не палить
Разом

.

Значення перевищує критичне . Істотність зв’язку доведено з імовірністю 0,95.

Корисною мірою при аналізі 4-клітинкових таблиць взаємної спряженості є відношення перехресних добутків або відношення шансів

Відношення шансів характеризує міру відносного ризику.
У нашому прикладі

.

Отже, імовірність легеневих хвороб у тих, хто палить, у 6 разів вища порівняно з тими, хто не палить.

Зауважимо, що методи аналізу таблиць взаємної спряженості можна використати і для кількісних ознак. Будь-які технічні перешкоди відсутні. Проте слід пам’ятати, що коефіцієнт спряженості оцінює лише узгодженість фактичного розподілу з пропорційним. При переставлянні рядків чи стовпців значення коефіцієнта С не зміниться. Міри щільності кореляційного зв’язку — коефіцієнт детермінації R² і кореляційне відношення h² — оцінюють не лише узгодженість частот, а й порядок, послідовність, в якій поєднуються різні значення ознак. Отже, ці характеристики зв’язку більш потужні. А загалом вибір методу вимірювання зв’язку і характеристик його щільності має ґрунтуватись на попередньому теоретичному аналізі суті явищ, характеру взаємозв’язків, наявній інформації.