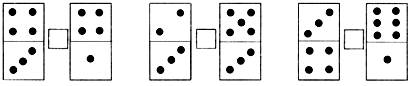
1. Составьте и назовите верные неравенства.
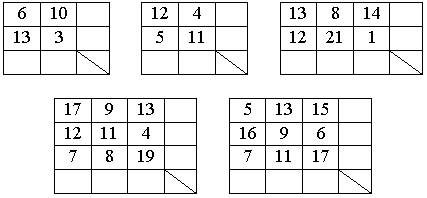
2. В этих таблицах надо сначала найти сумму в каждом столбце и записать её в нижней клетке столбца, затем найти сумму получившихся чисел и записать ее в левой части разделенной пополам клетки. Затем найти сумму в каждой строке, записать ее в свободной клетке той же строки, а потом сложить получившиеся суммы всех строк и записать результат во второй половине разделенной клетки. Что заметили?
II. Сообщение темы урока.
– Рассмотрите записи на доске.
12 + 6 36 + 22 24 + 3 32 + 3
19 – 3 48 – 13 13 + 6 25 + 2
– Какая запись является «лишней»? (36 + 28 и 48 – 13.)
– Сегодня на уроке мы будем учиться выполнять сложение и вычитание двузначных чисел.
III. Изучение нового материала.
Работа по учебнику.
– Прочитайте задачу 1. Сколько наклеек было у Коли? (2 пакетика по 10 наклеек в каждом и ещё 4 наклейки, то есть 24.)
– Сколько наклеек купила мама? (3 пакетика по 10 наклеек, то есть 30.)
– Сколько наклеек подарили Коле? (2 наклейки.)
– Сколько наклеек стало у Коли? (24 + 30 + 2 = 56.)
– Сколько единиц и сколько десятков в каждом из чисел 24 и 32?
(24 – 2 д. 4 ед.; 32 – 3 д. 2 ед.)
– Сколько единиц и сколько десятков у суммы этих чисел? (5 д. 6 ед.)
Задание 2.
– Место, где пишется цифра числа, называют разрядом.
Разряды идут справа налево – разряд единиц, разряд десятков, разряд сотен и т. д. Например, число 245 можно представить так:
| Сотни | Десятки | Единицы |
– Сколько единиц и сколько десятков в записи каждого числа?
(45 – 4 д. 5 ед., 68 – 6 д. 8 ед., 70 – 7 д., 94 – 9 д. 4 ед., 56 – 5 д. 6 ед.)
– Двузначные числа складывают так: единицы с единицами, десятки с десятками. Вычисления удобно записывать столбиком. При этом числа располагают друг под другом: единицы под единицами, десятки под десятками.
Показ примеров.
– Объясните, как сложить числа 23 и 45. Вычислите.
Задание 3. Выполните сложение чисел, записывая их в столбик.
– При вычитании числа тоже можно записывать в столбик: единицы под единицами, десятки под десятками. Сначала вычитают единицы, потом десятки. Читают запись сверху вниз.
Показ примеров.
– Объясните, как выполнили вычитание чисел 68 и 32.
Задание 4. Выполните вычитание двузначных чисел, записывая их в столбик.
Задание 5. Прочитайте задачи. Что известно? Что требуется узнать? Выполните краткую запись и решите задачи.
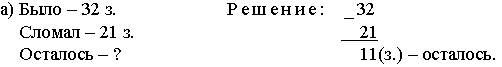
б) Было – 45 ор., 20 ор. Решение:
Испорченных – 30 ор. 1) 45 + 20 = 65 (ор.) – было.
Неиспорченных –? 2) 65 – 30 = 35 (ор.) – неиспорченных.
Задание 6. Работая в парах, найдите ошибки. Запишите правильно и вычислите.
14 38 60 43 123
21 5 9 20 24
35 33 69 23 147
Задание 7. Рассмотрите схему. Сколько путей ведёт от домика к колодцу? (4.)
– Найдите самый короткий путь:
1-й путь – 31 + 24 + 13 = 68.
2-й путь – 31 + 24 + 21 + 25 + 11 = 112.
3-й путь – 33 + 25 + 11 = 69.
4-й путь – 33 + 21 + 13 = 67.
IV. Итог урока.
– Назовите разряды двузначных чисел.
Урок 48
Сложение и вычитание двузначных чисел
Цели деятельности учителя: создать условия для развития умения выполнять сложение и вычитание двузначных чисел без перехода через разряд; способствовать совершенствованию умения решать арифметические задачи, восстанавливать равенства.
Планируемые результаты образования.
Предметные: умеют выполнять сложение и вычитание чисел в пределах 100 без перехода через разряд, решать текстовые задачи в одно действие на сложение и вычитание, составлять выражение по условию задачи.
Личностные: оценивают собственные успехи в освоении вычислительных навыков; имеют познавательную мотивацию, демонстрируют интерес к математическим заданиям повышенной трудности.
Метапредметные (критерии сформированности/оценки компонентов универсальных учебных действий – УУД): регулятивные: проверяют результаты вычислений с помощью обратных действий; планируют собственную вычислительную деятельность; познавательные: выполняют вычисления по аналогии; используют схемы при решении текстовых задач; моделируют условие задачи на схеме «целое – части»; ориентируются в таблицах, заполняют пустые клетки в таблице; расшифровывают задуманное число (соотносят результаты вычислений с буквами с помощью цифр); ориентируются в рисунках, схемах, цепочках вычислений; коммуникативные: высказывают своё мнение при обсуждении задания; при выполнении заданий в паре слушают друг друга, договариваются, объединяют полученные результаты при совместной презентации решения.
Ход урока






