 Формально ф-элемент (ф-подсистема) – некоторый оператор, преобразующий входные информационные сообщения в выходные. В связи с этим отношение эквивалентности двух ф-элементов следует понимать прежде всего в смысле эквивалентности соответствующих операторов F 1 и F 2.
Формально ф-элемент (ф-подсистема) – некоторый оператор, преобразующий входные информационные сообщения в выходные. В связи с этим отношение эквивалентности двух ф-элементов следует понимать прежде всего в смысле эквивалентности соответствующих операторов F 1 и F 2.
Однако поскольку функциональная структура не является тождественной организационной (физически материальной) структуре системы, то функциональная эквивалентность каких-либо элементов не гарантирует возможности (не говоря уже о целесообразности) реальной замены одного из них другим (другими). Иногда это попросту невозможно. Например, одну лампочку в 100 вт, выполняющую функцию освещения, нельзя заменить (в одном патроне) парой лампочек по 50 вт каждая, хотя с функциональной точки зрения ф-элемент, состоящий из пары таких лампочек, эквивалентен ф-элементу из одной 100-ваттовой лампочки. Поэтому при проведении тождественных преобразований функциональных схем наряду с отношением эквивалентности необходимо учитывать также и отношение взаимозаменяемости.

Операторы  и
и  подчиняются закону композиции Т, если они могут быть объединены в виде тройки
подчиняются закону композиции Т, если они могут быть объединены в виде тройки  которая отвечает определенной схеме соединения соответствующих им элементов.
которая отвечает определенной схеме соединения соответствующих им элементов.
Для ф-элементов (ф-подсистем), соответствующих операторам F 1 и F 2, композиция означает установление между ними определенной связи. Естественно, что не любые реальные элементы могут быть связаны между собой. Поэтому в процессе анализа функциональных схем на возможность возникновения подобных ситуаций должно быть обращено особое внимание. Иногда совместимость понимается в более узком смысле как согласованность соответствующих параметров (пространственно-временных ритмов, масштабов и т.п.).
Отношение совместимости как и отношение взаимозаменяемости обусловлено тем, что ф-элементы (ф-подсистемы) реализуются на множестве элементов и подсистем реальной структуры, которые обладают, помимо рассматриваемых функциональных свойств, еще целым набором других, влияющих на их взаимосвязи.
Композиции в функциональных структурах проявляются в виде последовательного, параллельного и встречно-параллельного (с обратной связью) соединения элементов. При этом последовательному соединению соответствует мультипликативный закон композиции; параллельному – аддитивный. Каждой из указанных схем может быть поставлено в соответствие операторное соотношение, представляющее собой формальную запись соответствующего закона композиции (рис. 2.3.2).
 |

а
 |

б
 |

в
 |

г
 |

д
Рис. 2.3.2. Схемы композиции ф-элементов:
а – последовательное соединение (мультипликативная композиция);
б – параллельное (аддитивная композиция в сочетании с композицией ветвления);
в – параллельное по входу (композиция ветвления); г – параллельное по выходу (аддитивная композиция); д – встречное (с обратной связью) соединение
(композиция ветвления в сочетании с аддитивной композицией)
 Выполнение отношения эквивалентности композиций на множестве ф-элементов (ф-подсистем) позволяет осуществлять тождественные преобразования функциональных структур (рис. 2.3.3). В приведенных на рисунке правилах ф-элемент
Выполнение отношения эквивалентности композиций на множестве ф-элементов (ф-подсистем) позволяет осуществлять тождественные преобразования функциональных структур (рис. 2.3.3). В приведенных на рисунке правилах ф-элемент  эквивалентен соответствующим композициям ф-элементов
эквивалентен соответствующим композициям ф-элементов  и
и  .
.
 | |||
 | |||

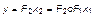

а
 | |||
| |||


б
 |


в
Рис. 2.3.3. Некоторые правила тождественных преобразований
функциональных структур:
+, -, о – символы операторного сложения, вычитания и умножения
В качестве практического примера использования правила а можно назвать объединение двух функций  = «написание рукописи статьи» и
= «написание рукописи статьи» и  = «печать» в одну функцию
= «печать» в одну функцию  = «электронный набор авторского текста». При этом в качестве входного информационного сообщения х выступает замысел (идея) статьи, а в качестве выходного сообщения у – соответствующий машинописный текст рукописи.
= «электронный набор авторского текста». При этом в качестве входного информационного сообщения х выступает замысел (идея) статьи, а в качестве выходного сообщения у – соответствующий машинописный текст рукописи.
Примером использования правила б будет сложение доходов в банке, полученных от кредитования двух клиентов.
Для правила в таким примером может служить технологический контроль качества какой-либо операции по выходному результату.
Последняя схема является идеализированной моделью соединения, допускающего бесконечное число актов обмена между элементами  и
и  по контуру обратной связи. Формально в операторной форме преобразование входного информационного сообщения в выходное может быть представлено в виде следующего бесконечного ряда параллельно-последовательных соединений (рис. 2.3.4); каждая из параллельных ветвей соответствует определенной кратности обхода контура обратной связи.
по контуру обратной связи. Формально в операторной форме преобразование входного информационного сообщения в выходное может быть представлено в виде следующего бесконечного ряда параллельно-последовательных соединений (рис. 2.3.4); каждая из параллельных ветвей соответствует определенной кратности обхода контура обратной связи.
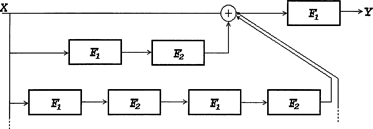
Рис. 2.3.4. Развернутая функциональная схема, эквивалентная схеме
встречного соединения (с обратной связью)
В операторной форме представленная схема может быть описана следующим образом:
 (2.3.11)
(2.3.11)
Здесь для сокращения записи использована степень, обозначающая соответствующую кратность обхода контура обратной связи.
Рассматривая полученный ряд как бесконечную геометрическую прогрессию, окончательно получим
 (2.3.12)
(2.3.12)
 Формально свойство ассоциативности аддитивного закона композиции может быть выражено следующим образом:
Формально свойство ассоциативности аддитивного закона композиции может быть выражено следующим образом:

или

Рис. 2.3.5. Тождественное преобразование функциональной структуры
на основе закона ассоциативности
Cвойство (закон) ассоциативности аддитивного закона композиции отвечает линейной суперпозиции результатов выполнения своих функций соответствующими ф-элементами (ф-подсистемами). Разумеется, в реальных ситуациях линейная суперпозиция выполняется далеко не всегда. И основная задача исследователя в данном случае заключается в определении условий ее выполнимости.
 Формально закон дистрибутивности операторов выражается как
Формально закон дистрибутивности операторов выражается как


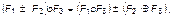
или как на рис. 2.3.6.
 |  | ||
Рис. 2.3.6. Тождественные преобразования функциональной структуры
на основе закона дистрибутивности
Примером подобного преобразования, в частности, может служить совместное или раздельное от специалистов F 1 и F 2 обсуждение результатов их работы руководством F 3 соответствующей организации.
 Формально закон коммутативности операторов может быть представлен в виде
Формально закон коммутативности операторов может быть представлен в виде  , или как на рис. 2.3.7.
, или как на рис. 2.3.7.

Рис. 2.3.7. Тождественное преобразование функциональной структуры
на основе закона коммутативности
Например, при приготовлении салата некоторые его компоненты могут добавляться в общую массу в любой последовательности, не меняя его гастрономических и эстетических качеств. Однако смена порядка таких действий, как  = «подумать» и
= «подумать» и  = «сделать», не всегда приводит к одинаковому результату. Впрочем, в некоторых ситуациях это может оказаться весьма полезным (например, когда ситуация достаточно рискованная, но сулит значительный эффект, и надо решать очень быстро).
= «сделать», не всегда приводит к одинаковому результату. Впрочем, в некоторых ситуациях это может оказаться весьма полезным (например, когда ситуация достаточно рискованная, но сулит значительный эффект, и надо решать очень быстро).

 Среди особых видов ф-элементов помимо тех, которым соответствуют операторы
Среди особых видов ф-элементов помимо тех, которым соответствуют операторы  , простые распределители, смесители, коммутаторы и т.п., существуют еще три, имеющие большое практическое значение. Это единичный, обратный и нулевой ф-элементы (операторы).
, простые распределители, смесители, коммутаторы и т.п., существуют еще три, имеющие большое практическое значение. Это единичный, обратный и нулевой ф-элементы (операторы).
Различают два типа единичных операторов: левый  и правый
и правый  . Их действие отражено на рис. 2.3.8.
. Их действие отражено на рис. 2.3.8.
Если пары операторов  и
и  коммутативны, то соответствующий функциональный оператор называется просто единичным. Заметим, что по сути дела каждая связь, не изменяющая формы и содержания сообщения, представляет единичный элемент (левый, правый или просто единичный).
коммутативны, то соответствующий функциональный оператор называется просто единичным. Заметим, что по сути дела каждая связь, не изменяющая формы и содержания сообщения, представляет единичный элемент (левый, правый или просто единичный).
 |

а


б
Рис. 2.3.8. Тождественные преобразования функциональных структур
с использованием единичных операторов
Аналогично этому существует два типа обратных ф-элементов: левый 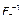 и правый
и правый  (рис. 2.3.9).
(рис. 2.3.9).
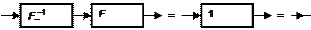 |

а
 |

б
Рис. 2.3.9 Тождественные преобразования функциональных структур
с использованием обратных операторов
Если пары операторов  и
и  коммутативны, то оператор
коммутативны, то оператор  называют просто оператором обратным оператору
называют просто оператором обратным оператору  .
.
В качестве примера прямого и обратного оператора можно привести следующие:  «перевозка груза G из пункта А в пункт В» и
«перевозка груза G из пункта А в пункт В» и  = «перевозка груза G из пункта В в пункт А».
= «перевозка груза G из пункта В в пункт А».
Аналогично операторам 1 и  определяется и нулевой оператор (иногда его называют еще нейтрализующим, или оператором «обрыва» (отключения) связи). Этот оператор, как правило, коммутативен с тем оператором, с которым вступает в композицию. Формально его действие равносильно обрыву соответствующей связи (рис. 2.3.10).
определяется и нулевой оператор (иногда его называют еще нейтрализующим, или оператором «обрыва» (отключения) связи). Этот оператор, как правило, коммутативен с тем оператором, с которым вступает в композицию. Формально его действие равносильно обрыву соответствующей связи (рис. 2.3.10).
 |

а
 |

б
Рис. 2.3.10. Тождественные преобразования функциональных структур
с использованием нейтрализующего (нулевого) оператора
 С учетом сказанного выше о свойствах бинарных отношений на множествах ф-элементов (ф-подсистем) и законов структурной организации можно сформулировать еще некоторые правила тождественных преобразований функциональных структур, имеющих большой практический интерес и связанных с операторами композиции
С учетом сказанного выше о свойствах бинарных отношений на множествах ф-элементов (ф-подсистем) и законов структурной организации можно сформулировать еще некоторые правила тождественных преобразований функциональных структур, имеющих большой практический интерес и связанных с операторами композиции  и точек ветвления, представляющих собой простые распределители (рис. 2.3.11).
и точек ветвления, представляющих собой простые распределители (рис. 2.3.11).

Рис. 2.3.11 Тождественные преобразования функциональных структур
с использованием свойства коммутативности операторов композиции:
а – перенос сумматора через ф-элемент слева; б – точки ветвления вправо;
в – сумматора вправо; г – перенос точки ветвления влево
Взаимные перестановки сумматора и точки ветвления подчиняются правилам, отраженным на рис. 2.3.12.

Рис. 2.3.12. Тождественные преобразования,
связанные с взаимным переносом сумматора и точки ветвления
Для того чтобы вышеизложенное не выглядело слишком формальным, рассмотрим следующий пример.
 Пусть несколько предприятий, расположенных на территории трех государств, по кооперации изготавливают некоторое сложное техническое изделие. Укрупненная схема технологических связей указанных предприятий показана на рис. 2.3.13.
Пусть несколько предприятий, расположенных на территории трех государств, по кооперации изготавливают некоторое сложное техническое изделие. Укрупненная схема технологических связей указанных предприятий показана на рис. 2.3.13.

Рис. 2.3.13. Схема технологических связей:
М01, М02 – механическая обработка деталей на заводах 1-го и 2-го государства;
Т01 и Т02 – термическая обработка на заводах 1-го и 2-го государства;
ХОЗ – химическая обработка деталей на заводах 3-го государства;
УС2 – узловая сборка на заводах 2-го государства;
Ф01 – функциональная отладка на заводах 1-го государства;
Сб1 – сборка на заводах 1-го государства,
Tij – транспортировка некоторых деталей из i-го государства в j-е
Если считать, что операторы Т23 и ХОЗ, ХОЗ и Т32, а также Т21 и ФО коммутативны, то приведенную выше функциональную схему можно преобразовать к виду рис. 2.3.14.

Рис. 2.3.14. Преобразованная функциональная структура
технологических связей
При выполнении тождественных преобразований было учтено, что
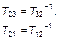
Очевидно, что полученная в результате тождественных преобразований схема существенно упростилась, поскольку из нее выпало несколько взаимообратных перевозок. Однако на преобразованной структуре мы обнаруживаем, что у нескольких функциональных операторов сменились индексы стран (заводов). И в этом смысле условие коммутативности здесь мы должны были формально записать в виде

Практически это означает, что указанные операции теперь должны выполняться на других заводах. Конечно, исключение встречных перевозок полезно прежде всего с экономической точки зрения, поскольку при этом не просто снижаются транспортные расходы, а транспортные расходы, связанные с межгосударственными перевозками (ликвидируются различные таможенные сборы).
Однако перенос той или иной функции с одного предприятия на другое должен быть технологически обеспечен (включая наличие специального оборудования и оснастки, квалифицированных кадров и т.п.).
В целом же решение подобного вопроса может быть формализовано в виде правил следующего типа:
 ,
,
где V – функция полезности рассматриваемой кооперативной системы.
 Если преобразование, выполняемое функциональным элементом
Если преобразование, выполняемое функциональным элементом  , не является необходимым для соответствующей системы, то последний может быть исключен из функциональной структуры системы. Неважно, наверное, на каких сваях строить дом – круглого или квадратного сечения. Поэтому операция превращения квадратных свай в круглые, вероятно, в принципе (если для этого нет каких-то других серьезных оснований) может быть исключена из технологической схемы строительства дома.
, не является необходимым для соответствующей системы, то последний может быть исключен из функциональной структуры системы. Неважно, наверное, на каких сваях строить дом – круглого или квадратного сечения. Поэтому операция превращения квадратных свай в круглые, вероятно, в принципе (если для этого нет каких-то других серьезных оснований) может быть исключена из технологической схемы строительства дома.
Исключение некоторых функций может происходить также по причине того, что в окружающей систему среде эта функция выполняется, и ее результатами система может воспользоваться. Следует однако заметить, что такое исключение, как правило, снижает уровень автономности системы.
 ?
?
Вопросы и упражнения
1. Дайте определение понятий функции, функционального элемента и функциональной подсистемы. Поясните взаимосвязь понятий функция, предназначение, миссия.
2. Обсудите взаимосвязь функциональной и организационной структур.
3. Охарактеризуйте основные функциональные свойства экономических и социально-политических систем.
4. Оцените надежность приведенных ниже функциональных схем:
 |
Числа означают вероятности успешного выполнения соответствующих функций.
5. Перечислите основные правила тождественных преобразований функциональных схем и поясните их роль при структуризации экономических и социально-политических систем.
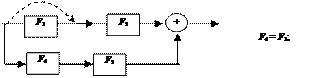
6. Осуществите тождественное преобразование приведенных ниже функциональных схем (пунктиром указана цель преобразования).
 | |||||
 | |||||
 |

ДИНАМИЧЕСКИЕ МОДЕЛИ СОЦИАЛЬНО–ПОЛИТИЧЕСКИХ И ЭКОНОМИЧЕСКИХ
ПРОЦЕССОВ
 3.1
3.1







