Концептуальные основы процессуального моделирования

Основной задачей процессуального моделирования является формирование модельного представления о динамическом образе ситуации как о системном процессе. Поскольку на процессы проявления сущности реальных систем оказывают влияние не только активные, но и пассивные (типа условий) факторы, выражение (3.1.3) следует несколько уточнить.

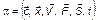, (3.1.3)

порождающем на анализируемом интервале времени Т соответствующее множество ситуационных историй Г.

В формуле (3.1.3): – вектор (множество) структурных признаков, характерных для рассматриваемой ситуации; 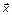– вектор (множество) независимых переменных признаков, описывающих возможные состояния объектов, участвующих в ситуации; – вектор (множество) кинематических признаков; – вектор (множество) системоформирующих конструктивных и деструктивных (динамических) факторов, могущих действовать в рамках рассматриваемой ситуации; t – время (точнее, упорядоченное множество существенных моментов времени); – вектор (множество) системообразующих конструктивных и деструктивных факторов (начальных и текущих (краевых) условий развития процесса).

Множества воздействий и условий, определяющих в конечном счете развитие системного процесса, включают в себя не только ситуационные, но и, как отмечалось выше, ценностные и информационные факторы. Последнее является чрезвычайно важным, поскольку поток информации, воспринимаемый системой, и ее знания в равной степени, как и ценности, состояния и структуры, формируют движение. Такое системно-физическое представление о процессах принципиальным образом отличается от чисто физического, ибо согласно этому представлению в уравнения движения также должны входить информация и знания.

В соответствии со сказанным системно-физический подход относительно движения можно трактовать как информационно-энергетический. Более того, важнейшей компонентой уравнений движения должна быть цель движения, поскольку ситуационные цели выступают в роли сигнального фактора, под действием которого происходит смена ценностных принципов (законов) движения.

Процессуальное моделирование заключается прежде всего в решении задачи синтеза динамического образа объекта или явления в виде соответствующей модели и технологическом ее использовании (собственно моделирование или эксплуатация модели) в интересах процессуального анализа.

Знание системного процесса позволяет в принципе ответить на вопрос о том, какие события могут произойти в рассматриваемой системе и ее окружении, и каким образом можно повлиять на них или хотя бы на их последствия.

Среди множества факторов, определяющих динамический образ системы, совершенно особое место занимают факторы-программы.

Фактор-программа – это фактор информационного зерна, фактор идеи (знания), способного прорасти при определенных условиях и вызвать к жизни качественно новые движения в соответствующей среде.

Практически каждая реальная программа способна породить в зависимости от складывающихся условий большое количество самых разнообразных ситуационных историй, олицетворяющих внешнее процессуальное проявление указанных программ.

Программа – внутренний закон движения. Разумеется, как всякий закон, она может не выполняться или выполняться с теми или иными отклонениями. Но это не уменьшает ее роли как фактора движения, т.е. фактора динамического в широком смысле этого слова.

Закономерности, порождаемые законом движения, зависят от тех условий, в которых он реализуется.

Все методы процессуального моделирования по своему функциональному назначению можно разбить на два множества: методы синтеза процессуальных моделей и методы эксплуатации синтезированных моделей (т.е. чисто технологические методы). С точки зрения языка описания все модели системных процессов могут быть разделены на формальные, формализованные и неформальные.

Рассмотрим некоторые из наиболее распространенных концепций формального описания подробнее.

Исходная идея кинематического описания чрезвычайно проста. Она заключается в построении на основе имеющейся информации зависимостей переменных признаков, характеризующих ситуацию от времени

. (3.1.4)

Следующий этап моделирования, как правило, является весьма сложным и трудно поддающимся формализации, поскольку его основная задача – в определении множества независимых признаков. С формальной точки зрения речь идет об определении ортогонального базиса в пространстве переменных (в пространстве состояний). Если модель динамического образа неформальна, то на данном этапе определяются независимые (т.е. причинно несвязанные) признаки (аспекты) рассматриваемого предмета.

В качестве иллюстрации возможностей кинематического анализа исследуем некоторые закономерности изменения переменных, характеризующих развитие социально-экономической ситуации в России за последние 25–30 лет. Соответствующие исходные статистические данные представлены в табл. 3.1.1.

Таблица 3.1.1

Статистические данные о развитии
социально-экономической ситуации в России
с 1970 г. по 1999 г. (по данным печати)

Показатели							1998(99)
Население, млн чел.	130,6	134,5	138,8	143,6	148,2	147,6	146,3
Национальное богатство, млрд дол.	–	–		3 379	4 130
Кол-во самоубийств, чел.	–	–	48 195	44 562	39 150	60 953	97 276
Кол-во чиновников, чел.	1 060	1 101	1 147	1 204	1 602	1 893	2 777
Доля доходов 20% наиболее бедных, %	7,8	9,5	10,1		9,8	5,5	6,2
Доля доходов 20% наиболее богатых, %	66,8	33,8	33,4		32,7	46,9	47,4

В качестве одной из координатных осей базиса фазового пространства возьмем переменную

где V – объем национального богатства; N – численность населения. В качестве других переменных выберем: x ₁– количество самоубийств (тыс. чел/год); x ₂ – количество чиновников (млн чел.); x ₃ – отношение доли доходов 20% наиболее богатых к доле доходов 20% наиболее бедных.

На рис. 3.1.4–3.1.5 представлены фазовые траектории изменения состояния российского общества за рассматриваемый период.

Рис. 3.1.4. Фазовая плоскость (х₀, х₂)

Рис. 3.1.5. Фазовые плоскости (х₀, х₁) и (х₀, х₃)

Как видно из приведенных на рис. 3.1.4 и 3.1.5 фазовых траекторий развития социально-экономической ситуации, в России после 1990 г. (крайние справа точки) наблюдается резко выраженная негативная тенденция практически по всем существенным признакам. Рассматривая указанные траектории, легко обнаружить довольно странные, на первый взгляд, закономерности: 1) чем меньше созданное удельное валовое национальное богатство (в расчете на душу населения), тем больше число чиновников, участвующих в распределении этого богатства; 2) чем меньше созданное удельное богатство, тем выше степень социального неравенства (тем больше пропасть между богатыми и бедными); 3) связь роста числа самоубийств с падением созданного национального богатства; данная закономерность носит явно социально-психологический характер и является вполне очевидной. Первые две закономерности следует, по-видимому, рассматривать с точки зрения влияния качества управления на благосостояние общества. Рост числа чиновников представляет собой, с одной стороны, попытку решения растущего разнообразия объекта управления чисто экстенсивным путем, а с другой – следствие падения уровня профессионализма управления, роста коррупции и т.п. Увеличение уровня социального расслоения также свидетельствует о снижении качества управления.

Кинематическое описание не позволяет еще в полной мере понять и оценить влияние тех или иных внешних факторов на состояние интересующей Наблюдателя системы. Более продуктивным в этом плане является использование так называемой модели «черного ящика», которая схематически изображена на рис. 3.1.6.

Рис. 3.1.6. Модель «черного ящика»

Концептуально модель «черного ящика» устанавливает взаимосвязь между выходными (наблюдаемыми) переменными исследуемого объекта и входными переменными ( 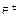-факторами) и ( -условиями). Вводя обозначение

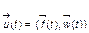, (3.1.5)

рассматриваемую модель формально можно записать в виде

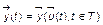. (3.1.6)

Согласно (3.1.6) объект выступает в роли преобразователя входных факторов в некоторую совокупность выходных факторов. Что происходит внутри данного структурного образования, как, каким образом вектор преобразуется в вектор , – исследователя не интересует. Ему важны только изменения, происходящие на границе, а не внутри объекта. Внутреннее состояние объекта является целью анализа только в той мере, в какой соответствующие переменные могут выступать в роли общих (выходных) переменных. Установив взаимосвязь между входом и выходом системы, Наблюдатель получает ответ на вопрос типа «Что? Где? Когда?», но еще не получает ответа на вопрос «Почему?» Тем не менее найденная информация сама по себе представляет значительный интерес, поскольку Наблюдателю становятся известными некоторые закономерности поведения объекта в соответствующих условиях, а значит, и определенные закономерности развития интересующей его ситуации.

В свете сказанного определение зависимостей типа (3.1.6) является, по существу, одним из видов факторного анализа. Однако поскольку переменные выхода сами часто выступают в роли некоторых факторов по отношению к рассматриваемому или каким-либо другим структурным образованиям, то указанный вид процессуального анализа целесообразно назвать фактор-факторным анализом.

В качестве иллюстрации факторного анализа проанализируем некоторые последствия дефолта августа 1998 г. В качестве объекта исследования выберем Кстовский район Нижегородской области (рис. 3.1.7).

Как видно из представленных данных, дефолт 1998 г. оказал весьма негативное влияние на социально-экономическую ситуацию в Кстовском районе. Наметившийся после кризиса начала 90-х гг. рост инвестиций I и падение естественной убыли населения 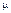после рассматриваемого события сменились противоположными тенденциями. В этом смысле названный дефолт явился динамическим фактором импульсного типа.

Рис. 3.1.7. Некоторые показатели социально-экономического развития
Кстовского района Нижегородской области:
I – годовой объем инвестиций; m – естественная убыль населения

Следующим шагом на пути более глубокого процессуального описания является концепция модели «серого ящика». В соответствии с этой концепцией объект исследования описывается не только входными 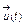и выходными признаками , но и переменными признаками , характеризующими внутреннее состояние объекта (рис. 3.1.8).

Рис. 3.1.8. Модель «серого ящика»

Переменные 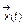могут выступать в роли факторов изменения состояния выходов, обусловленных внутренними движениями.

Проводя процессуальный анализ, исследователь пытается установить взаимосвязь выходных переменных и входных переменных 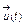с внутренними переменными состояния 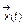. При этом объект анализа представляется в виде некоторого автомата, осуществляющего под влиянием внешних воздействий переходы из одних внутренних состояний в другие, из одних состояний выходов в другие. Формально автоматная модель может быть представлена в виде отображений

(3.1.7)

где V – пространство (множество возможных состояний входов; X – пространство (множество) возможных внутренних состояний объекта; Y – пространство (множество) возможных состояний выходов; T – множество существенных моментов времени.

Автоматные модели являются одним из наиболее простых видов имитационных моделей, описывающих движение системы с помощью некоторой совокупности правил (законов) перехода системы из одних состояний в другие.

Широкое распространение в процессуальном моделировании получили так называемые модели «динамической системы». Данная концепция заключается, по существу, в предположении, что скорости изменения выходных переменных (внешних реакций системы) есть некоторые функции от переменных, характеризующих соответствующую ситуацию. Динамическая система представляет собой систему (как правило, обыкновенных) дифференциальных или разностных уравнений вида

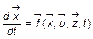, (3.1.8)

где – вектор переменных состояния; – вектор управлений; – вектор возмущений; t – время.

Модели «динамической системы» (динамические модели) относятся к классу имитационных, поскольку они реконструируют внутренне присущие реальным системам законы реагирования.

Особым видом автоматного представления являются так называемые модели систем массового обслуживания. Их реальными прообразами могут служить предприятия бытового обслуживания (столовые, рестораны, парикмахерские, гостиницы), банки, страховые компании, вокзалы и аэропорты, службы скорой помощи, противопожарные службы, системы противовоздушной и противокосмической обороны и т.д. Отличительная особенность указанных систем – наличие у них некоторого (вообще говоря, случайного) потока требований или заявок на обслуживание. В зависимости от типа системы и характера ситуации заявки могут поступать на обслуживание сразу или дожидаться своей очереди. Системы массового обслуживания в теории делятся на:

· одноканальные (одна касса, один мастер и т.д.);

· многоканальные (много параллельно работающих касс или мастеров);

· однофазные (процедура обслуживания включает одну операцию);

· многофазные (процедура обслуживания включает некоторое количество последовательно выполняемых операций).

Структурно система массового обслуживания (СМО) изображена на рис. 3.1.9.

Рис. 3.1.9. Модель системы массового обслуживания (СМО):
1 – входной поток заявок; 2 – очередь на обслуживание;
3, 4 – потоки обслуженных и отклоненных заявок

Согласно концепции СМО функционирование такого рода систем рассматривается только с точки зрения смены их функциональных состояний: прибор (оператор) занят обслуживанием очередной заявки, прибор (оператор) свободен и т.п. При этом поток заявок или требований на обслуживание рассматривается как некоторый поток событий. В теории СМО обычно рассматриваются однородные (т.е. состоящие из однотипных заявок) и ординарные потоки. Ординарность означает, что состояние системы является однозначной функцией времени: в один и тот же момент времени может произойти только одно событие.

Поток событий может быть регулярным, когда события происходят через равные промежутки времени, или нерегулярным. Для очень большого класса реальных систем поток событий можно рассматривать как нерегулярный (случайный). Обычно предполагается, что случайный поток образуют события, моменты наступления которых являются независимыми. Среди нерегулярных потоков важную группу составляют так называемые потоки без последействия (рис. 3.1.10).

Рис. 3.1.10

В потоке событий без последействия количество событий n ₂, случившихся за интервал времени r ₂, не зависит от числа событий n ₁, случившихся за некоторый предшествующий интервал времени r ₁. Отсутствие последействия свидетельствует об отсутствии влияния предшествующих событий на последующие. Очевидно, что реальные потоки событий, как правило, нестационарны. С течением времени их интенсивность меняется. Так, например, в течение суток весьма существенно меняется интенсивность транспортного потока на городских магистралях. Однако путем подбора соответствующих промежутков времени моделирования можно указанной нестационарностью пренебречь.

Если поток событий стационарен, ординарен и не имеет последействия, то он называется простейшим, или пуассоновским. Для пуассоновского потока вероятность того, что на интервале времени произойдет не более событий, равна

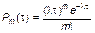, (3.1.9)

где – интенсивность потока (среднее количество событий, происходящих в единицу времени).

Вероятность того, что за время не произойдет ни одного события (), очевидно, равна

. (3.1.10)

В качестве основных показателей, характеризующих работу СМО, обычно принимаются:

· интенсивность обслуживания, т.е. среднее число заявок, удовлетворяемых в единицу времени;

· средняя длина очереди на обслуживание;

· среднее время ожидания заявкой обслуживания;

· вероятность отказа от обслуживания и т.д.

Рассмотрим простейшую одноканальную СМО, в которой потоки заявок на входе и поток обслуживания являются пуассоновскими. Указанные потоки реализуют стационарный случайный процесс без последствий. Такой процесс в научной литературе называется марковским. Вероятностные характеристики будущих состояний в марковском процессе зависят только от того состояния, в котором система находится в данный момент времени и не зависит от ее состояний в предшествующие моменты. Схема взаимосвязи возможных состояний такой системы может быть изображена в виде схемы рис. 3.1.11.

Рис. 3.1.11. Одноканальная СМО

В качестве реального прообраза данной СМО может служить, в частности, парикмахерская, в которой трудится всего лишь один мастер, обслуживающий в среднем в единицу времени 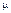клиентов. Предполагается, что заявки, пришедшие в систему в тот момент, когда она занята обслуживанием, становятся в очередь в порядке поступления. В этих предположениях система может находиться в следующих состояниях:

S ₀ – заявок в системе нет (она простаивает);

S ₁ – обслуживается одна заявка (очереди нет);

S ₂ – обслуживается одна заявка, и одна заявка находится в очереди; и т.д.

Если вероятности соответствующих состояний в момент времени обозначить через , , …,..., то значение последних через время можно определить следующим образом:

(3.1.11)

где – интенсивность потока заявок.

Переходя к пределу при , легко получить систему уравнений А.Н. Колмогорова:

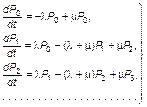(3.1.12)

В литературе процесс, описываемый системой 3.1.12, часто называют процессом «гибели–размножения».

Рассмотрим стационарный случай . Тогда из первого уравнения системы (3.1.12) будем иметь

, (3.1.13)

из последующих уравнений получим

Учитывая, что

, (3.1.14)

находим

Откуда

. (3.1.15)

Согласно (3.1.15) стационарный случай возможен, если

. (3.1.16)

Средняя длина очереди может быть найдена следующим образом:

Так как

то

или

. (3.1.17)

Вероятность простоя СМО, очевидно, равна значению ,

. (3.1.18)

Чем больше интенсивность обслуживания по сравнению с интенсивностью потока заявок, тем меньше средняя длина очереди, но тем больше среднее ожидаемое время простоя.

Вопросы и упражнения

7. Дайте определение понятия системный процесс. Приведите примеры проявления системных процессов в экономической и социально-политической сферах.

8. Дайте классификацию видов процессов.

9. Охарактеризуйте основные способы описания процессов.

10. Изобразите когнитивную схему (карту) взаимовлияний основных макроэкономических и микросоциальных факторов: объемы производства, цены, реальная зарплата, уровень инвестиций, уровень социальной напряженности и т.п.

11. Обсудите основную кибернетическую схему управления как функциональную структуру системного процесса.

12. Охарактеризуйте основные морфологические типы процессов. Приведите примеры морфологических и социально-политических процессов.

13. Обсудите методы описания состояния систем в фазовом пространстве.

14. Поясните модели Мальтуса и Ферхюльста.

3.2