Как показывает практический опыт, можно выделить три основных вида динамической согласованности:
· согласованность траекторий – выполнение отношения соответствия между временными последовательностями изменения значений признаков, характеризующих рассматриваемые процессы; пример: синхронный полет группы самолетов или синхронное плаванье группы спортсменов; движения объектов в этих случаях осуществляются по согласованным траекториям;
· согласованность событий – выполнение отношения соответствия между временными последовательностями событий, характеризующими рассматриваемые процессы; траекторной согласованности последних при этом в полной мере может и не быть; типичный пример: зачастую весьма схожие в событийном плане судьбы близнецов, составляющих, по-видимому, единые биоинформационные системы некой общей системы;
· согласованность по предельным состояниям (цели движения) – двигающиеся в ситуационном или фазовом пространстве по различным траекториям подсистемы некоторой системы в требуемый момент времени занимают заранее согласованное требуемое положение; типичный пример: скоординированые удары нескольких армий в направлении единого стратегически важного пункта или стыковка нескольких космических аппаратов, двигавшихся первоначально по совершенно различным траекториям.
 В качестве формальной модели, позволяющей оценить динамическую согласованность процессов изменения интегрируемых признаков х (t)и у (t), в предположении справедливости гипотезы о ее постоянстве, можно использовать показатель
В качестве формальной модели, позволяющей оценить динамическую согласованность процессов изменения интегрируемых признаков х (t)и у (t), в предположении справедливости гипотезы о ее постоянстве, можно использовать показатель
 (3.2.1)
(3.2.1)
где  , а – соответственно параметры временного сдвига и пространственной пропорции.
, а – соответственно параметры временного сдвига и пространственной пропорции.
Чем ближе величина 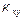 к единице, тем более сходными (согласованными с учетом сделанных выше оговорок) являются процессы изменения признаков х и у. Несогласованным процессам отвечает значение
к единице, тем более сходными (согласованными с учетом сделанных выше оговорок) являются процессы изменения признаков х и у. Несогласованным процессам отвечает значение 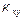 , равное нулю.
, равное нулю.
Величина 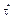 , соответствующая минимуму предела в выражении (3.2.1), характеризуют временную глубину согласования. Величина
, соответствующая минимуму предела в выражении (3.2.1), характеризуют временную глубину согласования. Величина  *, соответствующая минимуму этого предела, характеризует пропорцию этого согласования.
*, соответствующая минимуму этого предела, характеризует пропорцию этого согласования.
Для дискретных по времени процессов интеграл в выражении (3.2.1) заменяется суммой
 (3.2.2)
(3.2.2)
В качестве иллюстрации рассмотрим следующий пример.
 Пусть инвестиции в науку и образование х (t), взятые в % от ВВП, и приросты производительности труда у (t), взятой в % по отношению к предыдущему году, следующим образом зависели от времени (табл. 3.2.1).
Пусть инвестиции в науку и образование х (t), взятые в % от ВВП, и приросты производительности труда у (t), взятой в % по отношению к предыдущему году, следующим образом зависели от времени (табл. 3.2.1).
Таблица 3.2.1
| Признаки | t, годы | ||||||||||

| |||||||||||

|
Тогда, обозначая
 ,
,
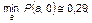
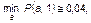

где
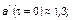


причем Р (1,2) = 0,04; Р (2,2) = 0,89, т.е. функция 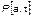 действительно имеет min по параметрам а, t. В нашем случае можно принять
действительно имеет min по параметрам а, t. В нашем случае можно принять  и
и 
Таким образом, приведенные в табл. 3.2.1 данные свидетельствуют о достаточно хорошей согласованности объемов инвестиций в науку и образование с темпами роста производительности труда. При этом коэффициент динамической согласованности

Согласно приведенным исследованиям изменение производительности труда запаздывает примерно на 2 года относительно изменения объемов инвестиций в науку и образование.
 Пусть в парламенте последовательно проходит несколько голосований, в которых члены фракций, голосуя солидарно «за», «против» или «воздерживаюсь», проявляют позиции соответствующих фракций. Если голосование не являлось бы солидарным, то позиции каждой фракции пришлось бы характеризовать не столь однозначно («за», «против» или «воздерживаюсь»), и вместо одного числа, отвечающего занятой позиции, пришлось бы пользоваться долями голосов членов фракции, поданных за каждый из трех возможных вариантов ответа.
Пусть в парламенте последовательно проходит несколько голосований, в которых члены фракций, голосуя солидарно «за», «против» или «воздерживаюсь», проявляют позиции соответствующих фракций. Если голосование не являлось бы солидарным, то позиции каждой фракции пришлось бы характеризовать не столь однозначно («за», «против» или «воздерживаюсь»), и вместо одного числа, отвечающего занятой позиции, пришлось бы пользоваться долями голосов членов фракции, поданных за каждый из трех возможных вариантов ответа.
Пусть результаты солидарного голосования выглядят так, как это показано в табл. 3.2.2.
Таблица 3.2.2
| Фракция | Вопрос | |||||
| А | -1 | -1 | ||||
| В | -1 | -1 | ||||
| С | -1 | |||||
| В | -1 |
В таблице числа 1, 0, -1 обозначают соответственно голосования «за», «воздерживаюсь» и «против». Для оценки динамической согласованности поведения фракций будем, предполагая, что совпадение фракционных решений типа «0–0» не означает совпадения позиций соответствующих фракций, пользоваться показателем
 (3.2.3)
(3.2.3)
где
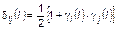 , (3.2.4)
, (3.2.4)
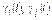 – значения признаков, приведенных в табл. 3.2.2, при голосовании по вопросу
– значения признаков, приведенных в табл. 3.2.2, при голосовании по вопросу 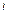 для фракций
для фракций  и
и 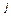 соответственно;
соответственно; 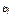 – коэффициент важности рассматриваемого вопроса;
– коэффициент важности рассматриваемого вопроса;  – общее количество проголосованных вопросов.
– общее количество проголосованных вопросов.
Если бы совпадения типа 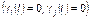 считались как совпадения позиций фракции
считались как совпадения позиций фракции  и
и 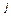 по вопросу
по вопросу 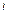 , то величину
, то величину  пришлось бы рассчитывать по несколько более громоздкой формуле
пришлось бы рассчитывать по несколько более громоздкой формуле
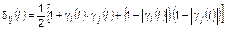 . (3.2.5)
. (3.2.5)
Подставляя данные табл. 3.2.2 в формулы (3.2.3)–(3.2.4), легко получить следующие оценки динамической согласованности поведения фракций при одинаковой важности всех вопросов  :
:



Более глубокая оценка, когда учитываются только совпадения, т.е. когда
 , (3.2.6)
, (3.2.6)
дает
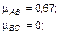
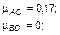

Пусть теперь вектор важности оценок  имеет следующие компоненты
имеет следующие компоненты

Тогда оценки согласованности поведения фракций уже будут такими:



Заметим, что все полученные нами оценки динамической согласованности не противоречат друг другу.
Рассмотренный подход может быть использован для изучения коалиционной структуры систем принятия коллективных решений. Аналогичным образом может быть и решена задача о лоббировании.
 Лоббирование проявляется в динамической согласованности выбора лоббирующей стороны с интересами лоббируемой. Для решения задачи о том, кто и кого лоббирует, необходимо составить матрицу, аналогичную матрице 3.2.3, дополненную строками, в которых бы числами -1, 0 и 1 отмечался характер интереса – отношения к положительному решению вопроса, поставленного на голосование, различных лоббируемых структур, а также строками, в которых бы указывались оценки важности рассматриваемых вопросов для указанных структур. Пусть, например, подобная матрица имеет вид табл. 3.2.3.
Лоббирование проявляется в динамической согласованности выбора лоббирующей стороны с интересами лоббируемой. Для решения задачи о том, кто и кого лоббирует, необходимо составить матрицу, аналогичную матрице 3.2.3, дополненную строками, в которых бы числами -1, 0 и 1 отмечался характер интереса – отношения к положительному решению вопроса, поставленного на голосование, различных лоббируемых структур, а также строками, в которых бы указывались оценки важности рассматриваемых вопросов для указанных структур. Пусть, например, подобная матрица имеет вид табл. 3.2.3.
Таблица 3.2.3
| Парламентарии | Голосования по вопросам | ||||||
| -1 | -1 | ||||||
| -1 | -1 | ||||||
| -1 | -1 | А | В | ||||
| -1 | -1 | ||||||
| Компании | Интерес | -1 | -1 | ||||
| Важность | 0,5 | 0,5 | |||||
| Интерес | -1 | -1 | -1 | ||||
| Важность | 0,5 | 0,5 |
Оценку динамической согласованности поведения отдельных парламентариев со стратегическими устремлениями соответствующих компаний проведем по формуле
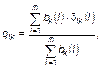 (3.2.7)
(3.2.7)
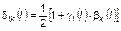 . (3.2.8)
. (3.2.8)
В результате получим




Предполагая, что общественные интересы имеют равномерное распределение (в смысле «за» и «против») по рассматриваемым вопросам, следует признать, что парламентарии, у которых для всех  величина
величина  близка к 0,5, не являются лоббистами каких-либо компаний. В нашем случае это парламентарий №3. Если же величина
близка к 0,5, не являются лоббистами каких-либо компаний. В нашем случае это парламентарий №3. Если же величина  для какой-то комбинации парламентарий–компания достаточно близка к 1, то данного парламентария следует рассматривать как лоббиста интересов соответствующей компании.
для какой-то комбинации парламентарий–компания достаточно близка к 1, то данного парламентария следует рассматривать как лоббиста интересов соответствующей компании.
3.2.2. Статическая согласованность
(стабильность, устойчивость)
Статическая согласованность – способность системы сохранять неизменными значения всех или части своих признаков в условиях действия тех или иных динамических факторов.
 Состояние (структура) реальной системы по некоторому признаку в момент времени t называется равновесным, если этот признак на интервале времени
Состояние (структура) реальной системы по некоторому признаку в момент времени t называется равновесным, если этот признак на интервале времени  , включающем t
, включающем t 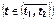 , сохраняет постоянным свое значение или совершает ограниченные по величине колебания, не вызывающие существенных и (или) необратимых структурных изменений и изменений состояния системы на указанном интервале времени
, сохраняет постоянным свое значение или совершает ограниченные по величине колебания, не вызывающие существенных и (или) необратимых структурных изменений и изменений состояния системы на указанном интервале времени  . Значения переменных, при которых достигается состояние равновесия, называются равновесными.
. Значения переменных, при которых достигается состояние равновесия, называются равновесными.
Состояние равновесия играет очень важную роль в жизни экономических и социально-политических систем. Это обусловлено прежде всего тем, что в этом состоянии кинематические признаки, характеризующие макродвижение системы, т.е. ее движение как единого целостного объекта, – зануляются, вследствие чего исчезает и инерция этого движения. В силу этого субъекту управления при попытке перевода системы в некоторое другое состояние уже не требуется тратить дополнительные ресурсы на преодоление указанной инерции.
 Равновесие реальной системы может быть полным или частичным в зависимости от степени охвата им соответствующих признаков. Оно может быть статическим (стационарным ) или динамическим в зависимости от того, сохраняет постоянным свое значение соответствующий признак (группа признаков) или совершает некоторые колебания. Заметим, что полное равновесие, т.е. равновесие, в котором бы отсутствовало всякое движение, недостижимо. Оно может существовать лишь на отдельном уровне иерархии состояний. Например, макроэкономическое равновесие есть лишь равновесие на уровне макроэкономических показателей. Наличие этого состояния не означает прекращения какой бы то ни было экономической жизни. Состояние полного равновесия – это состояние смерти, состояние «абсолютного нуля».
Равновесие реальной системы может быть полным или частичным в зависимости от степени охвата им соответствующих признаков. Оно может быть статическим (стационарным ) или динамическим в зависимости от того, сохраняет постоянным свое значение соответствующий признак (группа признаков) или совершает некоторые колебания. Заметим, что полное равновесие, т.е. равновесие, в котором бы отсутствовало всякое движение, недостижимо. Оно может существовать лишь на отдельном уровне иерархии состояний. Например, макроэкономическое равновесие есть лишь равновесие на уровне макроэкономических показателей. Наличие этого состояния не означает прекращения какой бы то ни было экономической жизни. Состояние полного равновесия – это состояние смерти, состояние «абсолютного нуля».
Равновесие может быть стабильным или нестабильным по отношению к действию внешних и внутренних возмущений.
Достаточно сложная система может обладать сравнительно большим или даже бесконечно большим числом различных состояний равновесия. Переход из одного состояния в другое происходит либо самопроизвольно (спонтанно) без каких-либо видимых причин, либо под действием явно проявляющихся возмущений.
 Стабильность системы есть способность к сохранению своего равновесия. Стабильность состояния (структуры) характеризуется длительностью t сохранения равновесия и (или) вероятностного
Стабильность системы есть способность к сохранению своего равновесия. Стабильность состояния (структуры) характеризуется длительностью t сохранения равновесия и (или) вероятностного  выхода из него за заданное время t. Стабильность системы может быть охарактеризована также величиной приобретаемой системой ценности или мощностью (энергией) внешнего воздействия, необходимых для нарушения равновесия.
выхода из него за заданное время t. Стабильность системы может быть охарактеризована также величиной приобретаемой системой ценности или мощностью (энергией) внешнего воздействия, необходимых для нарушения равновесия.
Вопрос о стабильности может быть поставлен значительно шире. Мы можем говорить не только о стабильности состояния или структуры, но и стабильности системы ценностей или системы знаний («Сколько стоит Ваша совесть, – не тридцать ли серебреников?»)
Чем больше интервал времени 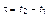 , чем выше вероятность
, чем выше вероятность  или чем выше необходимые для нарушения равновесия затраты ценностей, тем выше стабильность системы.
или чем выше необходимые для нарушения равновесия затраты ценностей, тем выше стабильность системы.
По отношению к рассматриваемому свойству все возможные состояния (структуры) делятся на стабильные, нестабильные или метастабильные.
Для системы, находящейся в стабильном состоянии или обладающей стабильной структурой, переход в некоторое другое стабильное состояние или некоторую другую стабильную структуру сопряжен с определенными затратами ценностей. Для системы, находящейся в нестабильном состоянии или обладающей нестабильной структурой, таких затрат не требуется.
Другими словами, в первом случае внешнее окружение расходует свои ценности на изменение состояния или структуры системы, а во втором оно может приобрести определенные ценности при таком изменении.
Время нахождения системы в метастабильном состоянии чаще всего зависит от скорости развития взаимодействий на микроуровне, а также от действия случайных внешних и внутренних факторов. Именно таким бывает состояние возбужденной толпы или перегретой жидкости. Достаточно незначительного, неуловимого колебания (толчка) и развитие событий приобретает взрывной характер.
Очевидно, что стабильность состояния равновесия обеспечивается соответствующими механизмами (законами) саморегуляции реальной системы. В основе указанных механизмов лежат определенные ценностные принципы (принципы полезности). Рассмотрим следующий пример.
 Рассмотрим рыночную экономику, в которой производится единственный продукт. На макроуровне в качестве такого продукта может, например, выступать валовой национальный продукт. Обозначим:
Рассмотрим рыночную экономику, в которой производится единственный продукт. На макроуровне в качестве такого продукта может, например, выступать валовой национальный продукт. Обозначим:  – объем выпуска указанного продукта в единицу времени;
– объем выпуска указанного продукта в единицу времени;  – сберегаемая часть этого продукта;
– сберегаемая часть этого продукта;  – потребляемая, т.е.
– потребляемая, т.е.
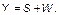
Если  – численность работающих, то, согласно первому предположению Кейнса, производственная функция может быть выражена следующим образом:
– численность работающих, то, согласно первому предположению Кейнса, производственная функция может быть выражена следующим образом:
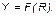 (3.2.9)
(3.2.9)
Кроме того, в теории экономического равновесия предполагается, что
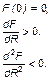
Т.е. производственная функция как функция числа работающих выпукла вверх.
Рынок труда. Предположим, что
 (3.2.10)
(3.2.10)
где  – ставка заработной платы;
– ставка заработной платы; 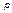 – цена продукта.
– цена продукта.
Рынок продукта. Второе допущение Кейнса заключается в предположении, что
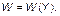
Таким образом,
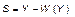
Откуда при относительно небольших отклонениях состояния рынка от равновесного приращение сберегаемого продукта можно выразить через приращение объема выпуска следующим образом:

Кейнсианская теория – это теория экономического равновесия. Смещение равновесного состояния экономики происходит под действием инвестиций. При этом инвестиции выступают в роли фактора повышения производственной активности. Если рынок находится в состоянии равновесия, то предположение фондообразующего продукта (инвестиций)  равно его спросу, т.е.
равно его спросу, т.е.
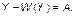
Таким образом, приращения объемов выпуска продукта  целиком определяется приращением объема инвестиций
целиком определяется приращением объема инвестиций 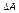 :
:

где по предположению 
Последнее выражение есть знаменитый мультипликатор Кейнса. Смысл его можно пояснить, если последнее выражение представить в виде

Согласно последнему выражению инвестиции как бы умножаются (множатся) в процессе производства, давая дополнительный объем продукта. Термин этот весьма удачен, поскольку в переводе с латыни multiplicatio означает умножение. Богатство умножается.
В теории Кейнса предполагается, что спрос на инвестиции полностью определяется нормой процента
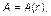
причем

Последние выражения вполне очевидны: чем выше норма процента, тем ниже спрос на инвестиции.
В условиях экономического равновесия сберегаемая часть продукта полностью сбалансирована с инвестициями:
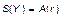 (3.2.11)
(3.2.11)
Рынок денег. Согласно Кейнсу, объем предложения денег  распределяется между операционным (т.е. обеспечивающим операции купли-продажи) спросом и спросом спекулятивным (когда деньги не пускаются в оборот из-за низкой нормы процента, а хранятся дома).
распределяется между операционным (т.е. обеспечивающим операции купли-продажи) спросом и спросом спекулятивным (когда деньги не пускаются в оборот из-за низкой нормы процента, а хранятся дома).
 (3.2.12)
(3.2.12)
где  – время запаздывания в процессе выполнения операций купли-продажи;
– время запаздывания в процессе выполнения операций купли-продажи;  – спекулятивный спрос на деньги.
– спекулятивный спрос на деньги.
Спекулятивный спрос обладает следующими свойствами:

Последнее выражение называется ловушкой ликвидности: если норма процента  меньше некоторой пороговой величины
меньше некоторой пороговой величины  , то владельцы денег теряют интерес к ценным бумагам (перестают их покупать и предпочитают хранить деньги дома, например в виде банкнот).
, то владельцы денег теряют интерес к ценным бумагам (перестают их покупать и предпочитают хранить деньги дома, например в виде банкнот).
Система уравнений (3.2.9)–(3.2.12) определяет состояние равновесия экономической системы, характеризуемое вектором равновесных значений своих переменных

В теории экономического равновесия доказано, что рассматриваемая в описанных выше предположениях система имеет единственное решение.
Модель Кейнса удобна для анализа возможных смещений состояния равновесия при возмущениях как переменных состояния, так и параметров экономической системы (в частности, величин  и
и  ).
).
Исследования данной модели показали, что отклонение цены от своего исходного равновесного значения определяются зависимостью

где все параметры  и
и  – возмущающие отклонения соответствующих переменных от их равновесных значений.
– возмущающие отклонения соответствующих переменных от их равновесных значений.
Из приведенного выражения, в частности, следует, что снижение инфляции может быть обеспечено за счет мероприятий, уменьшающих инвестиции  , стимулирующих сбережения
, стимулирующих сбережения  , снижающих ликвидность денег
, снижающих ликвидность денег  , увеличивающих спекулятивный спрос на деньги
, увеличивающих спекулятивный спрос на деньги  , снижающих заработную плату
, снижающих заработную плату 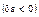 и увеличивающих объем выпуска
и увеличивающих объем выпуска 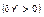 .
.
 Пусть платежеспособный спрос населения на некоторый продукт есть убывающая функция его цены:
Пусть платежеспособный спрос населения на некоторый продукт есть убывающая функция его цены:

Тогда прибыль компании, занимающейся продажей этого продукта, будет равна

где  – соответственно переменные и постоянные издержки. Компания стремится, очевидно, к получению максимальной прибыли. Формально, это означает
– соответственно переменные и постоянные издержки. Компания стремится, очевидно, к получению максимальной прибыли. Формально, это означает

Считая, что функция  имеет глобальный максимум, равновесная цена может быть найдена из условия
имеет глобальный максимум, равновесная цена может быть найдена из условия

или

где  – коэффициент эластичности спроса;
– коэффициент эластичности спроса;  – коэффициент, характеризующий норму прибыли. Решая последнее, можно определить равновесное значение цены на рассматриваемый продукт, т.е. такое ее значение, отклонение от которого в ту или другую сторону невыгодно компании.
– коэффициент, характеризующий норму прибыли. Решая последнее, можно определить равновесное значение цены на рассматриваемый продукт, т.е. такое ее значение, отклонение от которого в ту или другую сторону невыгодно компании.
 Практический опыт свидетельствует, что реальные системы обладают одной весьма важной закономерностью, которая получила название принципа Ле-Шателье: при изменении баланса динамических факторов, действующих на стабильно существующую систему, равновесие последней смещается в направлении, уменьшающем влияние этого изменения на ее стабильность.
Практический опыт свидетельствует, что реальные системы обладают одной весьма важной закономерностью, которая получила название принципа Ле-Шателье: при изменении баланса динамических факторов, действующих на стабильно существующую систему, равновесие последней смещается в направлении, уменьшающем влияние этого изменения на ее стабильность.
Так, обладающая меньшим боевым потенциалом группировка отступает (при разумном командовании) в направлении, которое, с одной стороны, позволяет ей по-возможности сохранить свои силы, а с другой – ослабить противостоящую группировку, растягивая ее коммуникацию и изматывая в арьергардных боях.
Данный принцип важно учитывать и при проведении различного рода социально-экономических реформ. И прежде чем воздействовать тем или иным образом на общество, необходимо изучить его внутреннюю природу, его возможные равновесные состояния. Ведь путем реализации реформы можно осуществить перевод этого общества из одного равновесного состояния в другое, ему «архетипически» присущее, а не придуманное реформаторами.
Устойчивость
 Устойчивость есть способность системы возвращаться в некоторое равновесное состояние после окончания действий внешних сил или внутренних возмущений. В общем случае устойчивость системы зависит от величины действовавшего на нее возмущения. Поэтому при формальном описании различают следующие виды устойчивости:
Устойчивость есть способность системы возвращаться в некоторое равновесное состояние после окончания действий внешних сил или внутренних возмущений. В общем случае устойчивость системы зависит от величины действовавшего на нее возмущения. Поэтому при формальном описании различают следующие виды устойчивости:
· относительно малых возмущений (устойчивость в малом);
· относительно больших, но конечных по величине возмущений (устойчивость в большом):
· относительно неограниченных по величине возмущений (абсолютная устойчивость).
Если изменение состояния системы описывается системой дифференциальных уравнений вида
 (3.2.13)
(3.2.13)
где 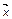 – вектор переменных состояния системы,
– вектор переменных состояния системы,  – вектор переменных возмущения, то об устойчивости состояния стационарного равновесия в малом можно судить по корням характеристического уравнения линеаризованной в точке равновесия системы (3.2.13).
– вектор переменных возмущения, то об устойчивости состояния стационарного равновесия в малом можно судить по корням характеристического уравнения линеаризованной в точке равновесия системы (3.2.13).
Пусть  есть некоторое состояние стационарного равновесия, т.е.
есть некоторое состояние стационарного равновесия, т.е.
 (3.2.14)
(3.2.14)
Тогда при достаточно малых отклонениях 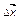 вектора
вектора 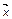 от
от  , обусловленного внешним возмущением, прекращающим свое действие в момент t = 0, функцию
, обусловленного внешним возмущением, прекращающим свое действие в момент t = 0, функцию  можно (если она достаточно «хороша» математически) разложить в ряд Тейлора, ограничиваясь первыми членами, т.е.
можно (если она достаточно «хороша» математически) разложить в ряд Тейлора, ограничиваясь первыми членами, т.е.
 , (3.2.15)
, (3.2.15)

В результате линеаризованная модель системы будет иметь вид
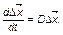 (3.2.16)
(3.2.16)
Характеристическое уравнение такой системы можно записать обычным образом
 (3.2.17)
(3.2.17)
где  – единичная матрица;
– единичная матрица;  – собственные значения характеристического уравнения.
– собственные значения характеристического уравнения.
При достаточно общих условиях справедлива следующая теорема.
 1. Если характеристическое уравнение линеаризованной системы уравнений имеет все корни
1. Если характеристическое уравнение линеаризованной системы уравнений имеет все корни  с отрицательными вещественными частями, то исходная нелинеаризованная система устойчива в малом.
с отрицательными вещественными частями, то исходная нелинеаризованная система устойчива в малом.
2. Если характеристическое уравнение линеаризованной системы уравнений имеет хотя бы один корень с положительной вещественной частью, то исходная нелинеаризованная система неустойчива в малом.
3. Если характеристическое уравнение линеаризованной системы уравнений имеет хотя бы один нулевой или пару чисто мнимых корней при условии, что все остальные корни имеют отрицательную вещественную часть, то поведение исходной нелинеаризованной системы не может быть определено по поведению линеаризованной.
Справедливость этой теоремы, по сути дела, следует из того, что решение линеаризованной системы уравнений может быть представлено в следующем виде
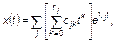 (3.2.18)
(3.2.18)
где  – кратность корня
– кратность корня 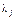 ;
;  – постоянный коэффициент, определяемый из начальных условий.
– постоянный коэффициент, определяемый из начальных условий.






