Численные решения некоторых задач линейной алгебры рассматривались в четвертой части настоящей главы. Большинство представленных там функций могут работать с символьными объектами. Рассмотрим далее наиболее распространенные из них.
Начнем с операций над векторами.
Функция length(a) используется для определения длины вектора a:
>> syms x y z
>> length([x y z])
ans =
Функция prod(a) вычисляет произведение элементов вектора a:
>> syms x y z
>> prod([x y z])
ans =
x*y*z
Функция sum(a) вычисляет сумму элементов вектора a:
>> syms x y z
>> sum([x y z])
ans =
x + y + z
Функция mean(a) вычисляет среднее арифметическое вектора a:
>> syms x y z
>> mean([x y z])
ans =
x/3 + y/3 + z/3
Функция dot(a,b) вычисляет скалярное произведение векторов a и b:
>> a1=sym('[x1 y1 z1]');
>> a2=sym('[x2 y2 z2]');
>> dot(a1,a2)
ans =
x2*conj(x1) + y2*conj(y1) + z2*conj(z1)
Функция cross(a,b) вычисляет векторное произведение векторов a и b:
>> a1=sym('[x1 y1 z1]');
>> a2=sym('[x2 y2 z2]');
>> cross(a1,a2)
ans =
[ y1*z2 - y2*z1, x2*z1 - x1*z2, x1*y2 - x2*y1]
Функция sort(a) выполняет упорядочивание элементов вектора a:
>> syms a b c d e f g h i j k
>> sort([k d j a i b g c e h f])
ans =
[ a, b, c, d, e, f, g, h, i, j, k]
Рассмотрим теперь с операции над матрицами.
Функция diag(a [, k]) возвращает квадратную матрицу с элементами вектора a на главной или на k-ой диагонали. Функция diag(A [, k]), где A – ранее определенная матрица, в качестве результата выдаст вектор-столбец, содержащий элементы главной или k-ой диагонали матрицы A. Имеем:
>> syms a b c d e f g h i j k
>> diag([a b c])
ans =
[ a, 0, 0]
[ 0, b, 0]
[ 0, 0, c]
>> diag([f,h],2)
ans =
[ 0, 0, f, 0]
[ 0, 0, 0, h]
[ 0, 0, 0, 0]
[ 0, 0, 0, 0]
>> diag([i,j],-2)
ans =
[ 0, 0, 0, 0]
[ 0, 0, 0, 0]
[ i, 0, 0, 0]
[ 0, j, 0, 0]
>> M=[a b c; d e f; h i k]
M =
[ a, b, c]
[ d, e, f]
[ h, i, k]
>> diag(M)
ans =
a
e
k
Функция repmat(A, n [, m]) формирует матрицу, состоящую из n на n или n на m копий матрицы A, причем если A – скаляр, то формируется матрица, элементы которой равны по величине значению A. Имеем:
>> syms a b c d e f g h i
>> A=[a b c; d e f; g h i]
A =
[ a, b, c]
[ d, e, f]
[ g, h, i]
>> repmat(A,2)
ans =
[ a, b, c, a, b, c]
[ d, e, f, d, e, f]
[ g, h, i, g, h, i]
[ a, b, c, a, b, c]
[ d, e, f, d, e, f]
[ g, h, i, g, h, i]
Функция reshape(A, m, n) возвращает матрицу размерности m на n, сформированную из A путем последовательной выборки по столбцам (если матрица A не имеет m на n элементов, то выдается сообщение об ошибке):
>> syms a b c d e f
>> A=[a b c; d e f]
A =
[ a, b, c]
[ d, e, f]
>> reshape(A,3,2)
ans =
[ a, e]
[ d, c]
[ b, f]
Функция cat(n, A, B [, C,...]) объединяет матрицы A и B или все входящие матрицы A, B, C и т.д. Имеем:
>> syms a b c d e f g h
>> A=[a b; c d]
A =
[ a, b]
[ c, d]
>> B=[e f; g h]
B =
[ e, f]
[ g, h]
>> cat(1,A,B)
ans =
[ a, b]
[ c, d]
[ e, f]
[ g, h]
>> cat(2,A,B)
ans =
[ a, b, e, f]
[ c, d, g, h]
Функция rot90(A [, k]) осуществляет поворот матрицы A на 90 градусов или на величину 90k, где k – целое число. Имеем:
>> syms a b c d e f g h i
>> A=[a b c; d e f; g h i]
A =
[ a, b, c]
[ d, e, f]
[ g, h, i]
>> rot90(A)
ans =
[ c, f, i]
[ b, e, h]
[ a, d, g]
Функция tril(A [, k]) формирует из матрицы A нижнюю треугольную матрицу, начиная с главной или с k-ой диагонали. Функция
triu(A [, k]) формирует из матрицы A верхнюю треугольную матрицу, начиная с главной или с k-ой диагонали. Имеем:
>> syms a b c d e f g h i
>> A=[a b c; d e f; g h i]
A =
[ a, b, c]
[ d, e, f]
[ g, h, i]
>> tril(A)
ans =
[ a, 0, 0]
[ d, e, 0]
[ g, h, i]
>> triu(A)
ans =
[ a, b, c]
[ 0, e, f]
[ 0, 0, i]
Функция size(A) определяет число строк и столбцов матрицы A, результатом ее работы является вектор [n m], где n – количество строк, а m – количество столбцов. Имеем:
>> syms a b c d e f
>> A=[a b c; d e f]
A =
[ a, b, c]
[ d, e, f]
>> size(A)
ans =
2 3
Функция prod(A [, k]) формирует вектор-строку (или вектор-столбец), в зависимости от значения k, каждый элемент которой является произведением элементов соответствующего столбца (или строки) матрицы A. Если значение параметра k в конструкции отсутствует, то по умолчанию вычисляются произведения столбцов матрицы. Очевидно, что результатом работы функции prod(prod(A)) является произведение всех элементов матрицы A. Имеем:
>> syms a b c d e f g h i
>> A=[a b c; d e f; g h i]
A =
[ a, b, c]
[ d, e, f]
[ g, h, i]
>> prod(A)
ans =
[ a*d*g, b*e*h, c*f*i]
>> prod(prod(A))
ans =
a*b*c*d*e*f*g*h*i
Функция sum(A [, k]) формирует вектор-строку (или вектор-столбец), в зависимости от значения k, каждый элемент которой является суммой элементов соответствующего столбца (или строки) матрицы A. Если значение параметра k в конструкции отсутствует, то по умолчанию вычисляются суммы столбцов матрицы. Результатом работы функции sum(sum(A)) является произведение всех элементов матрицы A. Имеем:
>> syms a b c d e f g h i
>> A=[a b c; d e f; g h i];
>> sum(A)
ans =
[ a + d + g, b + e + h, c + f + i]
>> sum(sum(A))
ans =
a + b + c + d + e + f + g + h + i
Функция mean(A [, k]) формирует вектор-строку (или вектор-столбец), в зависимости от значения k, каждый элемент которой является средним арифметическим значением элементов соответствующего столбца (или строки) матрицы A. Если значение параметра k в конструкции отсутствует, то по умолчанию вычисляются средние арифметические значения элементов столбцов матрицы. Результат работы функции sum(sum(A)) – среднее арифметическое значение всех элементов матрицы A. Имеем:
>> syms a b c d e f g h i
>> A=[a b c; d e f; g h i];
>> mean(A)
ans =
[ a/3 + d/3 + g/3, b/3 + e/3 + h/3, c/3 + f/3 + i/3]
>> mean(mean(A))
ans =
a/9 + b/9 + c/9 + d/9 + e/9 + f/9 + g/9 + h/9 + i/9
Функция sort(A) выдает матрицу того же размера, что и A, каждый элемент которой упорядочен по возрастанию. Имеем:
>> syms a b c d e f g h i
>> A=[d a i; b g c; e h f]
A =
[ d, a, i]
[ b, g, c]
[ e, h, f]
>> sort(A)
ans =
[ b, a, c]
[ d, g, f]
[ e, h, i]
Рассмотрим некоторые операции линейной алгебры.
Функция det(A) вычисляет определитель квадратной матрицы A, т.е.
>> syms a b c d e f g h i
>> A=[a b; c d]
A =
[ a, b]
[ c, d]
>> det(A)
ans =
a*d - b*c
>> B=[a b c; d e f; g h i]
B =
[ a, b, c]
[ d, e, f]
[ g, h, i]
>> det(B)
ans =
a*e*i - a*f*h - b*d*i + b*f*g + c*d*h - c*e*g
Функция trace(A) вычисляет след матрицы A, т.е. сумму элементов главной диагонали. Имеем:
>> syms a b c d e f g h i
>> A=[a b c; d e f; g h i]
A =
[ a, b, c]
[ d, e, f]
[ g, h, i]
>> trace(A)
ans =
a + e + i
Функция inv(A) вычисляет матрицу, обратную к матрице A. Имеем:
>> syms a b c d
>> A=[a b; c d]
A =
[ a, b]
[ c, d]
>> inv(A)
ans =
[ d/(a*d - b*c), -b/(a*d - b*c)]
[ -c/(a*d - b*c), a/(a*d - b*c)]
Функция eig(A) возвращает вектор собственных значений матрицы A. Обращение [M,D]=eig(A) позволяет получить матрицу M, столбцы которой являются собственными векторами матрицы A, и диагональную матрицу D, содержащую на главной диагонали соответствующие собственные значения матрицы A. Обращение eig(A,B), где A и B – квадратные матрицы, влечет вычисление вектора обобщенных собственных значений. Имеем:
>> syms x
>> A=[1 -1; a 2]
A =
[ 1, -1]
[ a, 2]
>> [M,D]=eig(A)
M =
[-((1-4*a)^(1/2)/2-3/2)/a-2/a, ((1-4*a)^(1/2)/2+3/2)/a-2/a]
[ 1, 1]
D =
[ 3/2 - (1 - 4*a)^(1/2)/2, 0]
[ 0, (1 - 4*a)^(1/2)/2 + 3/2]
Функция charpoly(A) возвращает вектор-строку коэффициентов характеристического полинома матрицы A. Имеем:
>> syms x
>> A=[1 -1; a 2];
>> charpoly(A)
ans =
[ 1, -3, a + 2]
С символьными матрицами можно выполнять действия аналогичные действиям с числовыми матрицами.
Пусть требуется вычислить квадрат матрицы
и показать, что матрица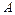 
является ортогональной.
Имеем:
>> syms alpha;
>> A=[cos(alpha) sin(alpha); -sin(alpha) cos(alpha)]
A =
[ cos(alpha), sin(alpha)]
[ -sin(alpha), cos(alpha)]
>> B=A^2
B =
[ cos(alpha)^2 - sin(alpha)^2, 2*cos(alpha)*sin(alpha)]
[ -2*cos(alpha)*sin(alpha), cos(alpha)^2 - sin(alpha)^2]
>> B=simplify(B)
B =
[ cos(2*alpha), sin(2*alpha)]
[ -sin(2*alpha), cos(2*alpha)]
>> I=simplify(A.'*A)
I =
[ 1, 0]
[ 0, 1]
Пусть требуется привести к жордановой форме матрицу
.
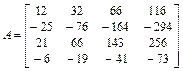Имеем:
>> A=sym([12 32 66 116; -25 -76 -164 -294;...
21 66 143 256; -6 -19 -41 -73])
A =
[ 12, 32, 66, 116]
[ -25, -76, -164, -294]
[ 21, 66, 143, 256]
[ -6, -19, -41, -73]
>> [V,J]=jordan(A)
V =
[ 4, -2, 4, 3]
[ -6, 8, -11, -8]
[ 4, -7, 10, 7]
[ -1, 2, -3, -2]
J =
[ 1, 1, 0, 0]
[ 0, 1, 0, 0]
[ 0, 0, 2, 1]
[ 0, 0, 0, 2]
>> V*J*inv(V)
ans =
[ 12, 32, 66, 116]
[ -25, -76, -164, -294]
[ 21, 66, 143, 256]
[ -6, -19, -41, -73]
Пусть требуется разложить по сингулярным числам рассмотренную выше матрицу .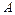
Имеем:
>> A=sym([12 32 66 116; -25 -76 -164 -294;...
21 66 143 256; -6 -19 -41 -73])
A =
[ 12, 32, 66, 116]
[ -25, -76, -164, -294]
[ 21, 66, 143, 256]
[ -6, -19, -41, -73]
>> [U,S,V]=svd(A);
>> double(U)
ans =
0.2830 0.9472 -0.1142 -0.0981
-0.7109 0.1073 -0.6415 -0.2675
0.6190 -0.3002 -0.5293 -0.4965
-0.1768 0.0334 0.5434 -0.8199
>> double(S)
ans =
486.7163 0 0 0
0 2.9955 0 0
0 0 0.4843 0
0 0 0 0.0057
>> double(V)
ans =
0.0724 0.7272 0.6016 0.3225
0.2205 0.5692 -0.3280 -0.7210
0.4747 0.2049 -0.6208 0.5893
0.8490 -0.3244 0.3810 -0.1698
>> double(U*S*V'-A)
ans =
1.0e-37 *
0.0588 0.1175 0 0.2351
0 0 0 0
0 0 0 0
0 0 0 -0.2351
