Упрощение выражений. Подстановки.

Рассмотрим вопросы, связанные с упрощением выражений и разного рода подстановками. Прежде всего, отметим, что для приведения коэффициентов при одинаковых степенях переменной или выражения используется команда collect; для разложения выражения на сумму и произведение простых сомножителей используется команда expand; для разложения полинома на множители используется команда factor; для упрощения выражений используются команды simplify и simple (устаревшая функция, которая будет исключена из MATLAB – идея алгоритма, реализованного в этой функции, но менее мощного по сравнению с реализованным в функции simplify, состоит в получении выражения, которое записывается меньшим количеством символов, чем исходное), которая выводит все возможные варианты преобразования выражения; для подстановки или замены переменных в выражении используются команды subs и subexr.

Перейдем к практическим примерам.

Пусть требуется упростить выражение

.

Имеем:

>> syms a x

>> f=a*log(x)-x*log(x)-x-a;

>> collect(f,log(x))

ans =

(a - x)*log(x) - a - x

Пусть требуется упростить выражение

.

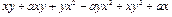Имеем:

>> syms x y a

>> f=x*y+a*x*y+y*x^2-a*y*x^2+x*y^2+a*x

f =

a*x + x*y + x*y^2 + x^2*y - a*x^2*y + a*x*y

>> collect(f,'x')

ans =

(y - a*y)*x^2 + (a + y + a*y + y^2)*x

>> collect(f,'y')

ans =

x*y^2 + (x + a*x - a*x^2 + x^2)*y + a*x

Поясним, что функция collect, обращение к которой в общем случае имеет вид

collect(expr [, var])

вычисляет коэффициенты полинома expr при степенях переменной var (раскрывает скобки и приводит подобные слагаемые), если второй параметр отсутствует, то по умолчанию выбирается переменная x.

Пусть требуется разложить выражение на сумму и произведение простых сомножителей. Имеем:

>> syms alpha beta

>> expand(cos(alpha+beta))

ans =

cos(alpha)*cos(beta) - sin(alpha)*sin(beta)

Пусть требуется разложить выражение 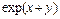на произведение простых сомножителей. Имеем:

>> syms x y

>> expand(exp(x+y))

ans =

exp(x)*exp(y)

Пусть требуется разложить выражение 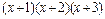на сумму и произведение простых сомножителей. Имеем:

>> syms x

>> f=(x+1)*(x+2)*(x+3)

f =

(x + 1)*(x + 2)*(x + 3)

>> expand(f)

ans =

x^3 + 6*x^2 + 11*x + 6

Пусть требуется разложить на множители полином 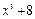. Имеем:

>> syms x

>> f=x^3+8

f =

x^3 + 8

>> factor(f)

ans =

(x + 2)*(x^2 - 2*x + 4)

Заметим, что если аргумент функции factor представляется собой целое число, то результатом работы этой функции будет произведение простых множителей такого числа.

Пусть требуется упростить выражение

.

Имеем:

>> syms x

>> f=(4-x^2)/(x+2)

f =

-(x^2 - 4)/(x + 2)

>> simplify(f)

ans =

2 - x

Пусть требуется упростить выражение

.

Имеем:

>> syms x

>> f=sin(x)^2+cos(x)^2

f =

cos(x)^2 + sin(x)^2

>> simplify(f)

ans =

Как уже отмечалось, функция subs(expr [, var1, var2]) выполняет операции подстановки, причем при обращении вида subs(expr) в символьном выражении expr все переменные заменяются их символьными значениями, определенными ранее. В результате обращения вида subs(expr [, var1]) все свободные символьные переменные из выражения expr заменяются на переменные из списка var1; в наиболее общем случае при обращении subs(expr [, var1, var2]) в символьном выражении expr осуществляется замена var1 на var2. Например, имеем:

>> x=1;

>> subs(x^2-2*x+1)

ans =

>> syms a b

>> p=sym('5*x^4-7*x^2+4')

p =

5*x^4 - 7*x^2 + 4

>> p=subs(p,a-b)

p =

5*(a - b)^4 - 7*(a - b)^2 + 4

>> subs(p,[a,b],[2,1])

ans =