В системе MATLAB методы численного интегрирования более высокого порядка точности реализуются функциями quad (метод Симпсона) и quadl (метод Гаусса-Лобатто). Следует отметить, что обе указанных функцию реализуют адаптивные алгоритмы, т.е. отсутствует необходимость контроля со стороны пользователя достигнутой точности вычисления интеграла посредством сопоставления результатов, полученных при использовании разных шагов интегрирования (эту процедуру адаптивные функции реализуют самостоятельно). Заметим, что функция quadl имеет более высокий порядок точности по сравнению с функцией quad, что позволяет выполнять интегрирование гладких функций с достаточно большими шагами интегрирования при сохранении точности (т.е., по сути, при меньшем объеме вычислительной работы). Функции функциями quad и quadl имеют достаточно длинные списки формальных параметров (как, впрочем, и многие другие функции в системе MATLAB), передаваемых в функцию при ее вызове. Минимальный список формальных параметров данных функций включает в себя три параметра: дескриптор подынтегральной функции, нижний и верхний пределы интегрирования:
q=quad(fun,a,b)
q=quadl(fun,a,b)
где fun – указатель на подынтегральную функцию; a и b – верхний и нижний пределы интегрирования.
Четвертый (дополнительный) параметр списка, задающий требуемую точность результата вычислений, является необязательным (по умолчанию точность принимается равной 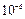 ).
).
Вычислим теперь рассмотренный выше интеграл, используя функции quad и quadl. Имеем:
>> f=inline('1-x+x.^2-x.^3','x');
>> TolX=1e-5;
>> [I,cnt]=quad(f,a,b,TolX)
I =
-12.749999999999996
cnt =
>> [I,cnt]=quadl(f,a,b,TolX)
I =
-12.750000000000002
cnt =
Второе из значений, возвращаемых данными функциями, – это количество точек, в которых пришлось вычислять подынтегральную функцию. Сопоставляя полученные показатели, можем заключить, что при интегрировании функции 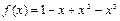 на отрезке
на отрезке 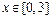 определенное преимущество имеет функция quad ввиду того, что для достижения заданной точности
определенное преимущество имеет функция quad ввиду того, что для достижения заданной точности  при использовании функции quad потребовалось меньшее количество вычислений подынтегральной функции (13 против 18). Вместе с тем, такое преимущество, разумеется, имеет место далеко не для всех функций. Так, например, при интегрировании функции
при использовании функции quad потребовалось меньшее количество вычислений подынтегральной функции (13 против 18). Вместе с тем, такое преимущество, разумеется, имеет место далеко не для всех функций. Так, например, при интегрировании функции 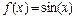 на отрезке
на отрезке 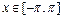 будем иметь:
будем иметь:
>> f=inline('sin(x)','x');
>> TolX=1e-5;
>> [I,cnt]=quad(f,-pi,pi,TolX)
I =
2.220446049250313e-16
cnt =
>> [I,cnt]=quadl(f,-pi,pi,TolX)
I =
2.015274060089494e-17
cnt =
т.е. в данном случае уже функция quadl более эффективна (установленная точность была достигнута за 18 итераций против 21 для функции quad).






