В первой части настоящей главы были рассмотрены арифметические операции над операндами типа double. Вместе с тем, помимо арифметических операций для операндов данного типа определены логические операции и операции отношения.
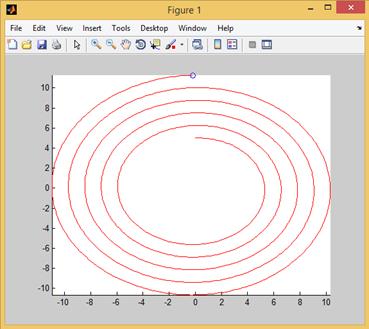
Рис. 2.12.20. Изображение траектории движения точки на плоскости.

Рис. 2.12.21. Изображение траектории движения точки в пространстве.
Операции отношения.
Операции отношения сравнивают между собой два операнда по величине. Способы записи этих операций представлены в таблице 2.13.1.
В случае истинности операции отношения ее величина (т.е. результат вычисления соответствующего выражения) равна 1, а в противоположном случае – 0. Приведем ниже пример вычислений в командном окне:
>> x=2; y=4; z=8;
>> x<y
ans =
>> x>y
ans =
>> y~=z
ans =
>> y==z
ans =
>> (x<y)+(y<=z)
ans =
Значение выражения x<y здесь равно единице (истина) в силу того, что величина переменной x в самом деле меньше величины переменной y. По этой же причине значение противоположного по смыслу выражения (x>y) равно нулю (ложь). Выражение y~=z является истинным, так как значение переменной y равное 4, не равно значению переменной z, равному 8. Последующее выражение y==z не является истинным, вследствие чего его значение равно 0. Далее, в силу истинности выражений x<y и y<=z (т.е. равенства единице их значений), получаем, что сумма значений этих выражений оказывается равной двум.
Операции отношения имеют более низкий приоритет по сравнению с арифметическими операциями, поэтому при вычислении последнего выражения в приведенном выше примере возникла необходимость заключения в скобки операций отношения x<y и y<=z. Исключительно важно не забывать про данное правило, так как отсутствие круглых скобок может привести к изменению результата, например:
>> a=1; b=2; c=4;
>> (b>a)+c
ans =
>> b>a+c
ans =
Функции, соответствующие операциям отношения (функции отношения), приведены в таблице 2.13.2. Соответствие функций операторам и ко-
Таблица 2.13.1. Обозначение операций сравнения.
| Операция | Обозначение в системе MATLAB | Справочно – обозначение в языке программирования FORTRAN (стандарт Fortran 90 и позднее). |
| Меньше | < | < |
| Меньше или равно | <= | <= |
| Больше | > | > |
| Больше или равно | >= | >= |
| Равно | == | == |
| Не равно | ~= | /= |
Таблица 2.13.2. Функции, соответствующие операциям отношения.
| Операция | Функция в системе MATLAB | Пример |
| Меньше | lt | lt(x,y) |
| Меньше или равно | le | le(x,y) |
| Больше | gt | gt(x,y) |
| Больше или равно | ge | ge(x,y) |
| Равно | eq | eq(x,y) |
| Не равно | ne | ne(x,y) |
мандам в системе MATLAB является одним из основных положений программирования, позволяющим одновременно использовать элементы как операторного, так и функционального программирования.
Логические операции.
Логические операции над вещественными числами (логические связки) обозначаются знаками, представленными в таблице 2.13.3.
Представленные в таблице 2.13.3 логические операторы предназначены для выполнения поэлементных логических операций над массивами одинаковых размеров. Заметим, что первые две операции, приведенные в таблице 2.13.2, являются двухоперандными (бинарными), а последняя операция является однооперандной (унарной). Соответственно знак ~ ставится перед операндом, а знаки & и | ставятся между операндами.
Логические операции трактуют свои операнды как «истинные» (не равные нулю) и «ложные» (равные нулю). Если оба операнда операции «Логическое И» истины (не равны нулю), то результат этой операции равен 1 («истина»), во всех же остальных случаях операция «Логическое И» возвращает значение 0 (ложь). Операция «Логическое ИЛИ» возвращает 0 (ложь) только лишь в случае, когда являются ложными (равными нулю) оба операнда). Операция «Логическое НЕ» инвертирует ложь на истину и наоборот, т.е. если ее операндом является ненулевое число, то эта операция возвращает 0, ну а если операнд нулевой, то тогда значением рассматриваемой операции будет единица.
Таблица 2.13.3. Обозначение логических операций (логических связок).
| Операция | Обозначение в системе MATLAB (логические операторы) | Справочно – обозначение в языке программирования FORTRAN (стандарт Fortran 90 и позднее). |
| Логическое И | & | .and. |
| Логическое ИЛИ | | | .or. |
| Логическое НЕ | ~ | .not. |
Таблица 2.13.4. Функции, соответствующие логическим операциям.
| Операция | Функция в системе MATLAB |
| Логическое И | and |
| Логическое ИЛИ | or |
| Логическое НЕ | not |
| Исключающее ИЛИ | xor |
Таблица 2.13.5. Работа логических операторов и функций.
| x | y | x&y and(x,y) | x|y or(x,y) | ~x (not x) | xor(x,y) |
Функции, соответствующие операциям сравнения и логическим операторам, приведены в таблице 2.13.4. Соответствие функций операторам и командам в системе MATLAB является одним из основных положений программирования, позволяющим одновременно использовать элементы как операторного, так и функционального программирования.
Более наглядное представление о работе логических операторов дает таблица 2.13.5, где в качестве операндов используются значения 0 и 1.
Помимо перечисленных в таблице 2.13.4, система MATLAB включает следующие функции:
any – возвращает 1, если в заданном векторе есть хотя бы один ненулевой элемент; если аргументом является матрица, результат выдается в виде вектора, элементы которого соответствуют столбцам заданной матрицы;
all – возвращает 1, если среди элементов исходного вектора нет нулевых; если аргументом является матрица, результат выдается в виде вектора, элементы которого соответствуют столбцам заданной матрицы.
Приведем пример:
>> A=[1 0 4; 5 0 0; 6 0 1]
A =
1 0 4
5 0 0
6 0 1
>> any(A)
ans =
1 0 1
>> all(A)
ans =
1 0 0
Приоритет операций.
Логические операции (кроме операции «Логическое НЕ», называемой также «операция отрицания») имеют самый низкий приоритет. Более подробные сведения о приоритете операций (в порядке убывания) в системе MATLAB приведена ниже:
1) Круглые скобки ();
2) Транспонирование (.’), транспонирование с комплексным сопряжением (’), возведение в степень (^), поэлементное возведение в степень (.^);
3) Унарный плюс (+), унарный минус (-), логическое отрицание (~);
4) Умножение и деление (.*,./,.\, *, /, \);
5) Сложение и вычитание (+, -);
6) Оператор сечения массива (:);
7) Операции отношения (<, <=, >, >=, ==, ~=);
8) Логическое И (&);
9) Логическое ИЛИ (|);
Отметим, что в одном выражении можно использовать все вышеперечисленные операции (арифметические, логические, операции сравнения), при этом последовательность выполнения операций определяется их расположением внутри выражения, их приоритетом и наличием круглых скобок (круглые скобки используются, в частности, для изменения приоритета операций в математических выражениях, причем степень вложения скобок не ограничивается).
Арифметические операции с комплексными числами реализуются в системе MATLAB точно также как и с вещественными числами (в соответствии с известными математическими правилами). Тоже самом относится и к операциям отношения «равно» и «не равно». Вместе с тем, как известно, операции сравнения комплексных чисел в математике не определены. Тем не менее, в системе MATLAB соответствующие операции с комплексными числами проводятся, но их значения определяются действительными частями рассматриваемых операндов:
>> x=1+2i; y=5i; z=7i;
>> x>y
ans =
>> y<=z
ans =
>> y>=z
ans =
Если один из операндов является скаляром, а другой – массивом, то происходит сравнение всех элементов второго операнда-массива со значением первого операнда-скаляра:
>> M=[-4 1; 0 2]
M =
-4 1
0 2
>> M>0
ans =
0 1
0 1
Таким образом, спектр применения операторов отношения в системе MATLAB шире, чем в традиционных языках программирования в силу того, что операндами являются не только числа (скаляры), но и векторы, матрицы, массивы. Операнды также могут быть символьными выражениями.






