Положение каждой точки в трехмерном пространстве, как известно, задается тремя координатами (в частности, в декартовой системе координат они традиционно обозначаются 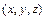 ). Набор точек, принадлежащий некоторой линии в пространстве, задается в виде трех векторов, которые содержат координаты точек по соответствующим координатным осям. Имена данных векторов указываются в списке формальных параметров функции plot3, которая выполняет проектирование соответствующей трехмерной линии на плоскость и строит соответствующее (результирующее) изображение. Следует подчеркнуть, что все сопутствующие вычисления и выбор необходимых параметров визуализации (пределы изменения переменных по осям координат, число графических и числовых меток, выбор цвета линии, цвета фона и т.д.) отображаемой зависимости будут сделаны автоматически в соответствии с общей концепцией высокоуровневой графики системы MATLAB.
). Набор точек, принадлежащий некоторой линии в пространстве, задается в виде трех векторов, которые содержат координаты точек по соответствующим координатным осям. Имена данных векторов указываются в списке формальных параметров функции plot3, которая выполняет проектирование соответствующей трехмерной линии на плоскость и строит соответствующее (результирующее) изображение. Следует подчеркнуть, что все сопутствующие вычисления и выбор необходимых параметров визуализации (пределы изменения переменных по осям координат, число графических и числовых меток, выбор цвета линии, цвета фона и т.д.) отображаемой зависимости будут сделаны автоматически в соответствии с общей концепцией высокоуровневой графики системы MATLAB.
Так, например, для построения пространственной (винтовой) спирали (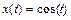 ,
, 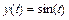 ,
, 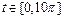 ) необходимо выполнить следующую последовательность команд (рис. 2.12.1):
) необходимо выполнить следующую последовательность команд (рис. 2.12.1):
>> t=0:pi/100:10*pi;
>> x=cos(t);
>> y=sin(t);
>> plot3(x,y,t);
>> grid on
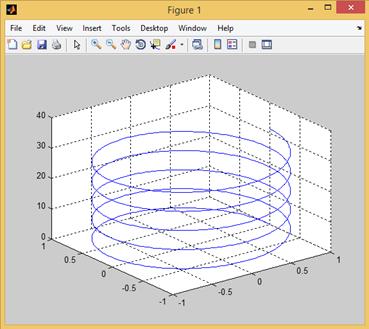
Рис. 2.12.1. Пример построения пространственной кривой.
Следует пояснить, что в результате задания функции
plot3(x,y,t)
система MATLAB построит трехмерную линию, координаты которой соответствуют элементам векторов x, y, и t.
Функция plot3, также как и функция plot, принимает дополнительный аргумент, задающий параметры графической линии (такие как цвет, тип линии и тип маркера, помечающего точки на графике). Так, например, для того, чтобы изобразить показанную на рис. 2.12.1 спираль в виде зеленой пунктирной линии, необходимо ввести следующую команду:
plot3(x,y,t,’g:’)
Функцию plot3, являющуюся трехмерным аналогом функции plot, можно применять и для отображения поверхностей. В таком случае в отличие от представленного примера, в списке формальных параметров указываются три матрицы одинакового размера. Далее высокоуровневая графическая подсистема MATLAB автоматически выполняет трехмерную визуализацию поверхности (набора линий в пространстве, количество которых будет соответствовать числу столбцов матриц) без сколь-либо существенных усилий со стороны пользователя.
Рассмотрим более подробно задание указанных матриц, используемых при визуализации поверхности. Пусть в точке с координатами  вычислено значение функции
вычислено значение функции  . Для всех таких точек
. Для всех таких точек 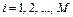 имеем соответствующие массивы точек. Соответствующие функции системы MATLAB проводят через эти точки гладкую поверхность и отображают ее проекцию на экран монитора компьютера. Следует отметить, что наиболее часто для вычисления аргументов используется разбиение области определения функции в виде прямоугольной сетки.
имеем соответствующие массивы точек. Соответствующие функции системы MATLAB проводят через эти точки гладкую поверхность и отображают ее проекцию на экран монитора компьютера. Следует отметить, что наиболее часто для вычисления аргументов используется разбиение области определения функции в виде прямоугольной сетки.
Для описания такой сетке в MATLAB необходимо создать две матрицы, которые будем обозначать здесь X и Y. Число строк данных матриц равно количеству узлов разбиения отрезка 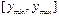 , а число столбцов – количеству узлов разбиения отрезка
, а число столбцов – количеству узлов разбиения отрезка 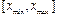 , при этом строки матрицы X одинаковые и содержат координаты узлов разбиения отрезка
, при этом строки матрицы X одинаковые и содержат координаты узлов разбиения отрезка 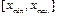 , а столбцы матрицы Y также одинаковые и содержат координаты узлов разбиения отрезка
, а столбцы матрицы Y также одинаковые и содержат координаты узлов разбиения отрезка  . Для формирования таких матриц используется функция meshgrid, имеющая следующий синтаксис:
. Для формирования таких матриц используется функция meshgrid, имеющая следующий синтаксис:
[X Y]=meshgrid(x,y)
где x и y – векторы, содержащие координаты узлов сетки (табличных точек) вдоль координат  и
и 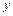 соответственно.
соответственно.
Заметим, что в частном случае, когда область определения функции представляет собой квадратную сетку т.е. 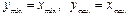 , то к функции meshgrid можно обратиться с одним аргументом:
, то к функции meshgrid можно обратиться с одним аргументом:
[X Y]=meshgrid(x)
В дальнейшем в каждом узле полученной таким образом прямоугольной сетки вычисляются значения функции 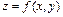 и сохраняются в соответствующей матрице Z.
и сохраняются в соответствующей матрице Z.
Очевидный проигрыш в памяти из-за повторяющихся строк в массиве X и повторяющихся столбцов в массиве Y компенсируются простотой и эффективностью вычисления значений визуализируемой функции в узлах сетки. Такой подход естественным образом гарантирует правильность сочетания координат x и y в узлах сетки.
Для построения поверхности в виде линий, получаемых в сечении поверхности плоскостями, параллельными плоскости 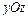 , как и в предыдущем примере используется функция plot3(X,Y,Z).
, как и в предыдущем примере используется функция plot3(X,Y,Z).
Построение поверхностей.
Помимо этой простейшей команды система MATLAB располагает еще рядом функций, позволяющих добиваться большей реалистичности при визуализации трехмерных графиков. Это, в частности, функции mesh (применяется для построения каркасной поверхности (или иначе проволочного каркаса (wire frame)), который образуется путем соединения точек поверхности с ближайшими соседями отрезками прямых), surf (применяется для построения каркасной поверхности, каждая клетка которой закрашивается определенным цветом, что позволяет значительно улучшить восприятие поверхности) и surfl, порождающие графические объекты типа surface. Каждая такая функция допускает множество разных вариантов вызова, отличающихся наборами входных параметров, и возвращает указатель на созданный объект.
Рассмотрим в качестве важного характерного примера задачу отображения функции 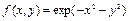 при
при  и
и 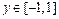 . Для ее решения воспользуемся последовательно функциями plot3, mesh, surf и surfl (соответствующие результаты представлены на рис. 2.12.2-2.12.5):
. Для ее решения воспользуемся последовательно функциями plot3, mesh, surf и surfl (соответствующие результаты представлены на рис. 2.12.2-2.12.5):
>> x=-2:0.1:2;
>> y=-1:0.1:1;
>> [X,Y]=meshgrid(x,y);
>> Z=exp(-X.^2-Y.^2);
>> plot3(X,Y,Z);
>> hmesh=mesh(X,Y,Z)
>> figure
>> mesh(X,Y,Z);
>> figure
>> surf(X,Y,Z);
>> figure
>> surfl(X,Y,Z);
Как видно из текста представленной программы, дескриптор объекта surface, возвращенный функцией mesh, был занесен в переменную hmesh. Для получения информации о типе графического объекта может быть использована команда get:
>> get(hmesh,'Type')
ans =
surface
Поясним, что разные ребра для лучшего восприятия «объемности изображения» автоматически окрашиваются в разные цвета. Эти цвета соответствуют значениям функции (по умолчанию более высоким (большим по величине) значениям функции соответствуют оттенки красного цвета, а более низким (меньшим по величине) – синего). В общем случае действует следующий алгоритм выбора цвета для вершин, ребер и граней поверхности. Все отображаемые элементы упорядочиваются по возрастанию координаты z характерной точки (для вершины – это табличная точка, для ребра – аппликата середины, для грани – аппликата точки пересечения диагоналей). Затем им присваиваются так называемые индексы цвета (одинаковым значениям z присваивается один и тот же индекс) и по этом индексу выбираются компоненты цвета из массива colormap, установленного в данный момент графического окна (объект типа Figure). Если пользователя не уст-
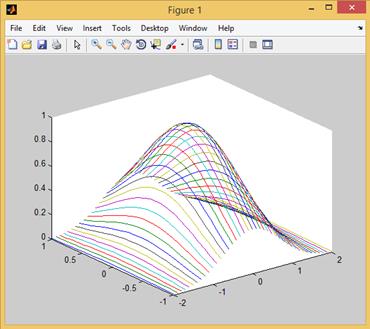
Рис. 2.12.2. Визуализация поверхности с использованием функции plot3.
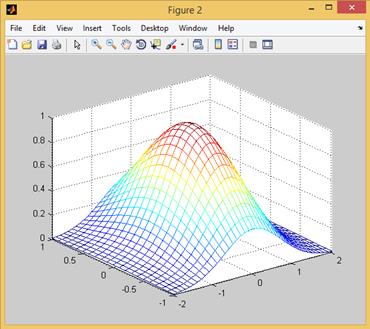
Рис. 2.12.3. Визуализация поверхности с использованием функции mesh.
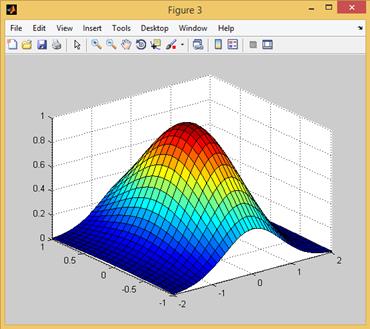
Рис. 2.12.4. Визуализация поверхности с использованием функции surf.
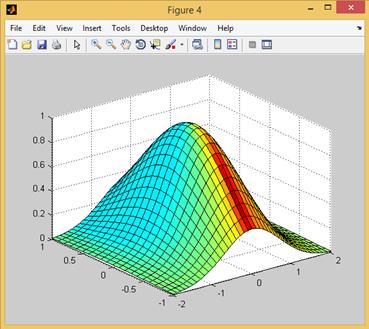
Рис. 2.12.5. Визуализация поверхности с использованием функции surfl.
раивает выбор цвета по высоте аппликаты, при создании поверхности можно в список аргументов добавить еще один массив той же размерности, что и X, Y, Z, который сформирует свойства CData и изменит способ окраски элементов поверхности.
При использовании функций mesh, surf и surfl, в отличие от функции plot3, осуществляется удаление невидимых линий поверхности. При необходимости отобразить невидимые ребра (сделать отображаемую поверхность «прозрачной») следует выполнить команду
>> hidden off
Возможно, что при отображении очень простых фигур типа пирамид или параллелепипедов невидимые линии могут оказаться полезными, однако на насыщенном изображении их присутствие лишь затрудняет восприятие. Для выключения режима отображения невидимых ребер (отмены режима «прозрачности) необходимо выполнить команду
>> hidden on
При использовании функции surf линии (ребра между гранями) поверхности отображаются черным цветом, а цвет каждой клетки зависит от значения функции (высоты) в некоторой характерной точке этой клетки.
С помощью команды shading способ закраски может быть изменен. Данная команда допускает использование следующих трех режимов:
flat – отображение линий поверхности (ребер) скрыто;
interp – отображение линий поверхности скрыто (создается видимость сплошной поверхности), цвета между соседними элементами поверхности сглажены;
faceted – возвращение к виду поверхности, заданному по умолчанию.
Таким образом у пользователя имеется возможность отобразить каждый участок поверхности, ограниченный четырьмя точками, своим цветом и отобразить между ними черные ребра (если иное не задано в свойствах объекта при вызове функции surf).
Если к имени функции mesh добавить букву c, то можно построить каркасную поверхность с линиями уровня функции, спроектированными на плоскость 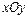 . При использовании функции meshc для решения задачи из предыдущего примера будем иметь (рис. 2.12.6):
. При использовании функции meshc для решения задачи из предыдущего примера будем иметь (рис. 2.12.6):
>> x=-2:0.1:2;
>> y=-1:0.1:1;
>> [X,Y]=meshgrid(x,y);
>> Z=exp(-X.^2-Y.^2);
>> meshc(X,Y,Z);
>> axis square;
Поясним, что команда (функция) axis square, задающая одинаковые размеры вдоль соответствующих осей координат (рис. 2.12.6).
Аналогично, если вместо функции surf применить функцию surfc, то можно построить закрашенную поверхность с линиями уровня, спроектированными на плоскость 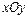 (рис. 2.12.7).
(рис. 2.12.7).

Рис. 2.12.6. Визуализация поверхности с использованием функции meshc.

Рис. 2.12.7. Визуализация поверхности с использованием функции surf.
>> x=-2:0.1:2;
>> y=-1:0.1:1;
>> [X,Y]=meshgrid(x,y);
>> Z=exp(-X.^2-Y.^2);
>> surfc(X,Y,Z);
Задание дополнительных параметров трехмерных графиков.
Заметим, что среди многочисленных параметров функций, создающих и отображающих поверхности, могут присутствовать пары типа
('Свойство', значение)
инициализирующие значения соответствующих свойств. Так, например, можно непосредственно изменить свойство EdgeColor построенного объекта типа surface, используя команду shading interp:
>> set(hmesh,'FaceColor','interp')
Разумеется, можно получить информацию о всех свойствах графического объекта типа surface:
>> hmesh=mesh(X,Y,Z)
hmesh =
174.0062
>> get(hmesh)
AlphaData: 1
AlphaDataMapping: 'scaled'
Annotation: [1x1 hg.Annotation]
CData: [21x41 double]
CDataMapping: 'scaled'
DisplayName: ''
EdgeAlpha: 1
EdgeColor: 'flat'
FaceAlpha: 1
FaceColor: [1 1 1]
LineStyle: '-'
LineWidth: 0.5000
Marker: 'none'
MarkerEdgeColor: 'auto'
MarkerFaceColor: 'none'
MarkerSize: 6
MeshStyle: 'both'
XData: [21x41 double]
YData: [21x41 double]
ZData: [21x41 double]
FaceLighting: 'none'
EdgeLighting: 'flat'
BackFaceLighting: 'reverselit'
AmbientStrength: 0.3000
DiffuseStrength: 0.6000
SpecularStrength: 0.9000
SpecularExponent: 10
SpecularColorReflectance: 1
VertexNormals: [21x41x3 double]
NormalMode: 'auto'
BeingDeleted: 'off'
ButtonDownFcn: []
Children: [0x1 double]
Clipping: 'on'
CreateFcn: []
DeleteFcn: []
BusyAction: 'queue'
HandleVisibility: 'on'
HitTest: 'on'
Interruptible: 'on'
Selected: 'off'
SelectionHighlight: 'on'
Tag: ''
Type: 'surface'
UIContextMenu: []
UserData: []
Visible: 'on'
Parent: 173.0057
XDataMode: 'manual'
XDataSource: ''
YDataMode: 'manual'
YDataSource: ''
CDataMode: 'auto'
CDataSource: ''
ZDataSource: ''
Поверхность графика можно трактовать как материальную поверхность с определенными физическими свойствами по отражению света, которые следует задавать явным образом. Ввиду того, что разные материалы, очевидно, по-разному отражают падающие лучи, можно подобрать некоторый материал, чтобы получить наилучшее (с точки зрения пользователя) изображение. В частности, используя функцию с аргументом copper
>> colormap(copper)
можно установить цвет поверхности, аналогичный цвету медной поверхности (copper – в переводе с английского языка «медь»). Последующее использование команд
>> surfl(X,Y,Z)
>> shading interp
позволяет получить вполне реалистично выглядящий и наглядный график, представленный на рис. 2.12.8.
Поясняя данный пример, перечислим ниже стандартные цветовые палитры (colormap), доступные для использования: cool (оттенки голубого и пурпурного цветов), gray (оттенки серого цвета (традиционно используется, в частности, при подготовке графика к печати на черно-белом принтере)), hot (плавное изменение следующих цветов: белый – желтый – оранжевый – красный – черный), hsv (плавное изменение цветов радуги), jet
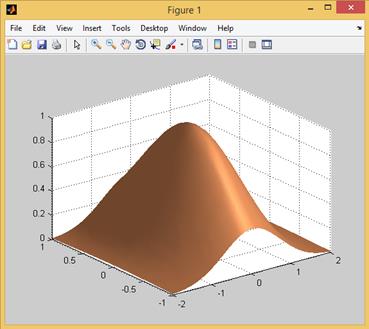
Рис. 2.12.8. Визуализация поверхности с использованием функции surfl (режим цветовой палитры – copper; режим shading interp).
(плавное изменение следующих цветов: красный – желтый – зеленый – голубой – синий (используется по умолчанию)), copper (дополнительная палитра с оттенками медного цвета), autumn (дополнительная палитра с плавным изменением следующих цветов: желтый – оранжевый – красный), winter (дополнительная палитра с оттенками синего и зеленого цветов), summer (дополнительная палитра с оттенками желтого и зеленого цветов), spring (дополнительная палитра с оттенками желтого и пурпурного цветов), pink (дополнительная палитра с оттенками коричневого цвета).
Изменять цветовую палитру можно с помощью функции
colormap('название палитры')
С помощью команды colormap('default') можно вернуться к палитре, используемой по умолчанию.
Использованная в вышеприведенном примере функция surfl «предполагает», что в пространстве расположен некоторый источник света, освещающий поверхность. Такие поверхности выглядят более естественно, если заменить заданную по умолчанию палитру цветов такими палитрами как gray, copper, pink и задать сглаживание цветов на графике с помощью команды shading interp.
Вообще, многие приемы оформления трехмерных графиков совпадают с теми, что уже были представлены ранее при рассмотрении двумерных графиков функций, зависящих от одной переменной. В частности, для масштабирования удобно использовать функцию axis, в которую в трехмерном случае следует передать три пары скалярных аргументов:
axis([xmin xmax ymin ymax zmin zmax])
Для трехмерных графиков, как и для двумерных, можно использовать функции xlabel (выводит название оси  ), ylabel (выводит название оси
), ylabel (выводит название оси  ), zlabel (выводит название оси
), zlabel (выводит название оси  – относительно новая, но очевидная команда), title (добавляет заголовок графика) и legend (добавляет легенду графика), а также наносить отметки на осях координат посредством функции set. Для того, чтобы разместить несколько трехмерных графиков в одном графическом окне, можно воспользоваться функцией subplot.
– относительно новая, но очевидная команда), title (добавляет заголовок графика) и legend (добавляет легенду графика), а также наносить отметки на осях координат посредством функции set. Для того, чтобы разместить несколько трехмерных графиков в одном графическом окне, можно воспользоваться функцией subplot.
К числу достаточно эффективных методов дополнительного оформления трехмерных графиков можно отнести возможность вызвать функцию mesh с суффиксом z, т.е. функцию meshz, использование которой приводит к построению «графика с пьедесталом» – из каждой граничной точки каркасной поверхности опускается перпендикуляр на плоскость  и при достаточно мелком шаге сетки создается впечатление «занавеса, опущенного по краям изображения». Так, например, график, приведенный на рис. 2.12.9, строится с помощью следующей последовательности команд:
и при достаточно мелком шаге сетки создается впечатление «занавеса, опущенного по краям изображения». Так, например, график, приведенный на рис. 2.12.9, строится с помощью следующей последовательности команд:
>> [X,Y]=meshgrid(-2:0.1:2);
>> Z=X.*exp(-X.^2-Y.^2);
>> colormap(gray)
>> meshz(X,Y,Z)
Все трехмерные графики, рассмотренные ранее, визуализировались, по сути, лишь из одной точки обзора, т.е. оси координат  ,
, 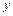 и
и  на изображении всегда были ориентированы (повернуты) одинаково. Тем не менее, в системе MATLAB имеется возможность, изменяя точку обзора, рассмотреть созданное изображение с разных сторон.
на изображении всегда были ориентированы (повернуты) одинаково. Тем не менее, в системе MATLAB имеется возможность, изменяя точку обзора, рассмотреть созданное изображение с разных сторон.
Точка обзора – это позиция, с которой пользователь видит трехмерное изображение. Расположение точки обзора определяется двумя параметрами: азимутом /az/ (т.е. углом, изменение которого означает вращение плоскости 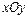 вокруг оси
вокруг оси 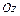 против хода часовой стрелки (отсчитывается от оси, противоположной
против хода часовой стрелки (отсчитывается от оси, противоположной 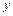 , в направлении против часовой стрелки)) и углом возвышения /el/ (т.е. углом между отрезком, направленным из начала координат в точку обзора и плоскостью
, в направлении против часовой стрелки)) и углом возвышения /el/ (т.е. углом между отрезком, направленным из начала координат в точку обзора и плоскостью 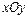 ). Заметим, что расстояние от точки обзора до изображения при этом не учитывается.
). Заметим, что расстояние от точки обзора до изображения при этом не учитывается.
Заметим, что по умолчанию для функций mesh, surf и surfl установлены значения az=-37.5 (градусов) и el=30 (градусов). Убедиться в этом можно посредством функции view, обратившись к ней должным образом:
>> [az,el]=view
az =
-37.5000
el =

Рис. 2.12.9. Визуализация функции 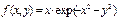 с «пьедесталом».
с «пьедесталом».
Функция view также позволяет изменить положение точки обзора, причем возможны сразу несколько вариантов ее вызова, в частности:
view([az,el])
view([x,y,z])
view(2)
view(3)
В первом случае входными аргументами рассматриваемой функции являются значения азимута и угла возвышения, во втором – декартовы координаты точки обзора, а третий и четвертый варианты обращения позволяют вернуться к значениям азимута и угла возвышения, принятых по умолчанию для двумерных (az=0 (градусов) и el=90 (градусов)) и трехмерных изображений (az=-37.5 (градусов) и el=30 (градусов)) соответственно.
В частности, если после построения представленного на рис. 2.12.9 «графика с пьедесталом» выполнить команду view([-20,25]), то график изменит свой вид, поскольку мы уменьшили угол возвышения с 30 градусов до 25 градусов, а угол азимута изменили с -37.5 градусов на значение равное -20 градусам. В результате точка получаем, что обзора графика находится больше сбоку и преимущественно вдоль одной из независимых координат (рис. 2.12.10).
Отметим, что рассмотренную операцию изменения ориентации в пространстве трехмерного графика можно выполнить и с помощью панели инструментов графического окна.
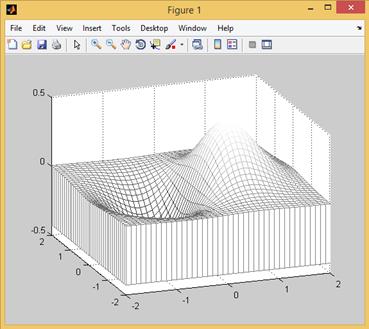
Рис. 2.12.10. Поверхность, задаваемая функцией 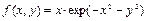 (угол возвышения 25 градусов, азимутный угол -20 градусов).
(угол возвышения 25 градусов, азимутный угол -20 градусов).
Рассмотрим в качестве еще одного важного характерного примера задачу отображения функции 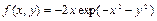 при
при  и
и 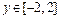 при условии расположения точки обзора снизу (рис. 2.12.11):
при условии расположения точки обзора снизу (рис. 2.12.11):
>> [X,Y]=meshgrid(-2:0.1:2);
>> Z=-2*X.*exp(-X.^2-Y.^2);
>> surf(X,Y,Z)
>> view(-37.5,-20)
Альтернативным и существенно более простым способом изменения точки обзора в системе MATLAB является использование специальной кнопки на панели инструментов графического окна Figure.
Если в графическом окне отображается трехмерный график, эта кнопка ( ) имеет название Rotate 3D (вращать трехмерное изображение). Если навести указатель мыши на данную кнопку, щелкнуть левой кнопкой мыши по кнопке Rotate 3D, после чего навести указатель мыши на трехмерное изображение, нажать левую кнопку мыши, и, не отпуская ее перемещать указатель мыши по экрану, то положение фигуры (и соответственно точки обзора) будет меняться, а в левой нижней части графика будут отображаться значение параметров az и el, соответствующие текущему положению трехмерной фигуры. Если же навести указатель на фигуру и щелкнуть по правой кнопке мыши, то отобразиться контекстное меню с командами, поз-
) имеет название Rotate 3D (вращать трехмерное изображение). Если навести указатель мыши на данную кнопку, щелкнуть левой кнопкой мыши по кнопке Rotate 3D, после чего навести указатель мыши на трехмерное изображение, нажать левую кнопку мыши, и, не отпуская ее перемещать указатель мыши по экрану, то положение фигуры (и соответственно точки обзора) будет меняться, а в левой нижней части графика будут отображаться значение параметров az и el, соответствующие текущему положению трехмерной фигуры. Если же навести указатель на фигуру и щелкнуть по правой кнопке мыши, то отобразиться контекстное меню с командами, поз-
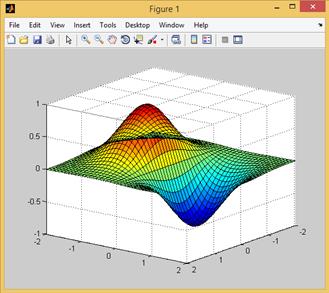
Рис. 2.12.11. Вид поверхности 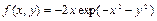 снизу.
снизу.
воляющими вернуться к положению фигуры по умолчанию, а также выбрать одну из трех проекций графика (на плоскости 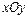 ,
, 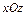 ,
, 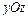 ). В частности, на рис. 2.12.12 показана проекция поверхности на плоскость
). В частности, на рис. 2.12.12 показана проекция поверхности на плоскость 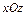 (это положение соответствует команде view(0,0)).
(это положение соответствует команде view(0,0)).
Для того, чтобы установить точное соответствие между цветом, отображенным на трехмерном графике, и значением функции, можно воспользоваться командой colorbar, после вызова которой рядом с графиком появляется столбик с текущей цветовой палитрой и цифрами, определяющими значения функции. Этой команде соответствует кнопка ( ) Insert Colorbar (добавить цветовую палитру) на панели инструментов графического окна Figure. Так, например, если ввести в командное окно команду colorbar либо щелкнуть на кнопке Insert Colorbar левой кнопкой мыши графическое окно с трехмерным изображением, показанным на рис. 2.12.11, примет вид, представленный на рис. 2.12.13.
) Insert Colorbar (добавить цветовую палитру) на панели инструментов графического окна Figure. Так, например, если ввести в командное окно команду colorbar либо щелкнуть на кнопке Insert Colorbar левой кнопкой мыши графическое окно с трехмерным изображением, показанным на рис. 2.12.11, примет вид, представленный на рис. 2.12.13.
Еще большей реалистичности в визуализации трехмерных объектов можно добиться, задавая параметры освещенности для объекта.
Для проявления отдельных участков поверхности графика, отображаемого в системе MATLAB, имеется возможность включения дополнительных источников освещения, реализованных в виде графических объектов типа light. Свет от такого рода источников смешивается с рассеянным фоновым освещением (Ambientlight), цвет и сила которого встроены в виде
характеристик в объекты axes (свойство AmbientLightColor) и surface (свойство AmbientLight).
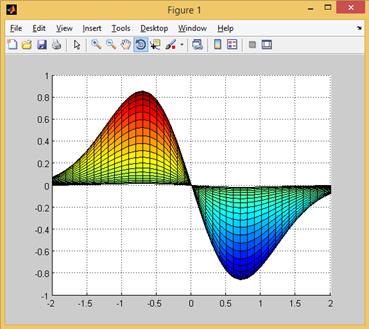
Рис. 2.12.12. Проекция 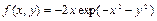 на плоскость
на плоскость 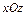 .
.

Рис. 2.12.13. Добавление цветовой палитры на график.
В частности, для примера, показанного на рис. 2.12.9,
>> hsurfl=surfl(X,Y,Z)
hsurfl =
174.0081
>> set(hsurfl,'FaceLighting','phong','FaceColor','interp');
>> set(hsurfl,'AmbientStrength',0.5);
>> light('Position',[1 0 0],'Style','infinite');
>> light('Position',[1 0 0],'Style','infinite');
задаются такие свойства поверхности (свойства графического объекта типа surface), которые влияют на результирующее изображение при использовании дополнительных источников света. Далее создается такой источник в позиции, определяемой его свойством Position, и испускающий параллельные лучи (style=infinite, т.е. бесконечно удаленный источник).
Кроме того, можно задать цвет дополнительного источника подсветки поверхности графика (свойство Color объекта light). Для того, чтобы сделать источник света более сильным, следует продублировать его несколько раз, создавая все новые источники в том же месте и с теми же свойствами, при этом дескрипторы каждого вновь создаваемого источника света нужно запоминать в соответствующих переменных. При соблюдении этого условия впоследствии можно будет с помощью функции set изменять их свойства и суммарную силу (мощность) света (для выключения конкретного источника необходимо задать его свойство Color равным black), добиваясь желаемого внешнего вида графика. По сути, именно здесь проявляется важное преимущество системы MATLAB при работе с ней в интерактивном режиме: можно оперативно оценить достигнутый результат и, если что-то не нравится, выполнить отдельные части работы (а не всю работу) заново.
По умолчанию источник света (например, при использовании команды surfl) имеет следующие координаты: az=7.5 (градусов) и el=30 (градусов). Положение источника света можно также изменить, задав дополнительным входным аргументом функции surfl вектор, включающий новые значения азимута и угла возвышения. Так, например, можно задать источник света, совпадающий с точкой обзора можно, использовав следующий набор команд:
>> [az,el]=view
>> surfl(X,Y,Z,[az,el])
Создать источник света можно иначе и другим альтернативным способом – посредством функции camlight. Ниже перечислены некоторые возможные варианты вызова последней:
camlight headlight – создать источник освещения, расположение которого совпадает с точкой обзора;
camlight right (или camlight) – создать источник освещения, находящийся правее и выше точки обзора;
camlight left – создать источник освещения, находящийся левее и выше точки обзора;
camlight(az,el) – создать источник информации с требуемыми координатами.
Многократное применение функции camlight с разными аргументами позволяет создать несколько источников света, расположенных в разных местах. Как уже отмечалось выше, вид освещенной поверхности во многом зависит от материала поверхности. В системе MATLAB управлять свойствами материала, из которого создана поверхность, позволяет функция material, однако результаты вызова указанной функции становятся видны лишь после освещения поверхности источником света. Ниже указаны несколько вариантов вызова функции material:
material shiny – сделать поверхность блестящей;
material dull – сделать поверхность матовой;
material metal – сделать поверхность «металлической»;
material default – задать свойства материала поверхности, принятые по умолчанию.
Система MATLAB позволяет рассмотреть трехмерный объект, изображенный в графическом окне, не только с разных сторон, но и с различного расстояния (по аналогии с объективом виртуальной камеры). Имеются возможности для приближения и удаления трехмерных изображений, их перемещения и вращения относительно различных координатных осей (т.е., по сути, выполнять роль виртуального фотографа). Реализовать перечисленные функции позволяет специальная панель инструментов графического окна, которая называется Camera (камера) и показана на рис. 2.12.14.

Рис. 2.12.14. Панель инструментов Camera.
Для того, чтобы отобразить данную панель следует выбрать в инструментальной панели графического окна раздел меню View, после чего отметить в ниспадающем меню пункт Camera Toolbar. После щелчка на нужной кнопке на этой панели управлять положением объекта и камеры можно либо с помощью мыши, либо посредством клавиш со стрелками. Заметим, впрочем, что все команды панели инструментов Camera продублированы в контекстном меню, которое можно открыть, щелкнув на изображении правой кнопкой мыши.
Итак, для трехмерных графиков также существует возможность изменять свойства условной камеры, фиксирующей сцену с графиком: можно менять положение этой камеры, расстояние от стены, а также свойства ее объектива (это достаточно мощные способы влиять на изображения). Изменять свойства указанной камеры можно с помощью дескрипторного метода.
Как уже отмечалось ранее, графическим объектом, соответствующим поверхности трехмерного графика функции, является объект типа surface. Дескриптор такого объекта возвращается функциями mesh, surf и surfl. Объект surface, в свою очередь, является наследником объекта axes, получить описатель которого можно, вызвав функцию gca, которая возвращает описатель текущего объекта axes (в ситуациях, когда создано несколько таких объектов, перед вызовом функции следует щелкнуть левой клавишей мыши на выбираемом объекте axes). Получив описатель, далее можно функцией set изменять свойства объекта axes, в частности, свойства, связанные с камерой, фиксирующей сцену с расположенным на ней трехмерным графиком. Приведем список соответствующих свойств объекта axes:
>> hA=gca
hA =
173.0057
>> get(hA)
ActivePositionProperty = outerposition
ALim = [0.1 10]
ALimMode = auto
AmbientLightColor = [1 1 1]
Box = off
CameraPosition = [-18.2628 -23.8006 4.33013]
CameraPositionMode = auto
CameraTarget = [0 0 0]
CameraTargetMode = auto
CameraUpVector = [0 0 1]
CameraUpVectorMode = auto
CameraViewAngle = [10.3396]
CameraViewAngleMode = auto
CLim = [-0.428838 0.428838]
CLimMode = auto
Color = [1 1 1]
CurrentPoint = [ (2 by 3) double array]
ColorOrder = [ (7 by 3) double array]
DataAspectRatio = [4 4 1]
DataAspectRatioMode = auto
DrawMode = normal
FontAngle = normal
FontName = Helvetica
FontSize = [10]
FontUnits = points
FontWeight = normal
GridLineStyle =:
Layer = bottom
LineStyleOrder = -
LineWidth = [0.5]
MinorGridLineStyle =:
NextPlot = replace
OuterPosition = [0 0 1 1]
PlotBoxAspectRatio = [1 1 1]
PlotBoxAspectRatioMode = auto
Projection = orthographic
Position = [0.13 0.11 0.775 0.815]
TickLength = [0.01 0.025]
TickDir = out
TickDirMode = auto
TightInset = [0.0571429 0.05 0.0303571 0.00238095]
Title = [175.006]
Units = normalized
View = [-37.5 30]
XColor = [0 0 0]
XDir = normal
XGrid = on
XLabel = [176.006]
XAxisLocation = bottom
XLim = [-2 2]
XLimMode = auto
XMinorGrid = off
XMinorTick = off
XScale = linear
XTick = [-2 -1 0 1 2]
XTickLabel =
-2
-1
XTickLabelMode = auto
XTickMode = auto
YColor = [0 0 0]
YDir = normal
YGrid = on
YLabel = [177.006]
YAxisLocation = left
YLim = [-2 2]
YLimMode = auto
YMinorGrid = off
YMinorTick = off
YScale = linear
YTick = [-2 -1 0 1 2]
YTickLabel =
-2
-1
YTickLabelMode = auto
YTickMode = auto
ZColor = [0 0 0]
ZDir = normal
ZGrid = on
ZLabel = [178.006]
ZLim = [-0.5 0.5]
ZLimMode = auto
ZMinorGrid = off
ZMinorTick = off
ZScale = linear
ZTick = [-0.5 0 0.5]
ZTickLabel =
-0.5
0.5
ZTickLabelMode = auto
ZTickMode = auto
BeingDeleted = off
ButtonDownFcn =
Children = [174.009]
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [1]
Selected = off
SelectionHighlight = on
Tag =
Type = axes
UIContextMenu = []
UserData = []
Visible = on
Построение линий уровня.
Для построения так называемых контурных графиков в MATLAB предусмотрены функции как contour, contourf и contour3, с помощью которых строятся так называемые линии уровня или изолинии. Под последними понимаются кривые, получающиеся в результате пересечения поверхности 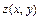 с плоскостями
с плоскостями 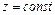 . Эти линии можно спроектировать на одну плоскость, и получить двумерное изображение, а можно воспроизвести как пространственные кривые и получить трехмерное изображение. Наглядным примером двумерных изображений изолиний являются линии рельефа поверхности на топографических картах (по последним, как известно, можно легко локализовать впадины и вершины, оценить их глубины и высоты, особенно, если в разрывах изолиний проставлены числовые значения соответствующих уровней).
. Эти линии можно спроектировать на одну плоскость, и получить двумерное изображение, а можно воспроизвести как пространственные кривые и получить трехмерное изображение. Наглядным примером двумерных изображений изолиний являются линии рельефа поверхности на топографических картах (по последним, как известно, можно легко локализовать впадины и вершины, оценить их глубины и высоты, особенно, если в разрывах изолиний проставлены числовые значения соответствующих уровней).
В частности, с использованием функции contour можно строить проекции линий уровня на плоскости 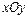 . Необходимо отметить, что данная функция имеет несколько вариантов вызова. Так, например, если обратиться к ней с тремя аргументами (в данном случае X, Y, и Z – матрицы одинаковой размерности, задающие координаты узлов сетки, в которых определены аппликаты поверхности).
. Необходимо отметить, что данная функция имеет несколько вариантов вызова. Так, например, если обратиться к ней с тремя аргументами (в данном случае X, Y, и Z – матрицы одинаковой размерности, задающие координаты узлов сетки, в которых определены аппликаты поверхности).
>> [X,Y]=meshgrid(-2:0.1:2);
>> Z=-2*X.*exp(-X.^2-Y.^2);
>> colormap(gray)
>> contour(X,Y,Z)
то получим график, представленный на рис. 2.12.9 (заметим, что в представленном фрагменте использована серая полутоновая матрица цветности (colormap(gray)).
Заметим, что если область определения поверхности квадратная и шаги по осям  и
и 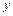 совпадают, то вместо пары аргументов X, Y может быть задан только один массив.
совпадают, то вместо пары аргументов X, Y может быть задан только один массив.
Для того, чтобы такой график стал более информативным, целесообразно возле каждой линии уровня отобразить значение, которое соответствует значению функции. Для этого используется функция clabel(C,h), при вызове которой необходимо задать два входных параметра – матрицу C, содержащую информацию о линиях уровня (эту матрицу можно рассматривать как таблицу, состоящую из двух строк – первая колонка задает значение уровня изолинии и количество содержащихся в ней точек, следом располагается указанное количество пар 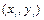 с координатами точек изолинии; вслед за первой изолинией в том же формате располагается информация о второй изолинии и т.д. (данный массив требуется, когда необходимо оцифровывать изолинии, т.е. включать в разрыв линии значение ее уровня), и вектор h, представляющий собой набор указателей на созданные графические массивы (также требуется при оцифровке изолиний). Требуемые для функции clabel параметры автоматически генерирует функция contour, если ее вызвать с двумя входными аргументами (параметрами) C и h:
с координатами точек изолинии; вслед за первой изолинией в том же формате располагается информация о второй изолинии и т.д. (данный массив требуется, когда необходимо оцифровывать изолинии, т.е. включать в разрыв линии значение ее уровня), и вектор h, представляющий собой набор указателей на созданные графические массивы (также требуется при оцифровке изолиний). Требуемые для функции clabel параметры автоматически генерирует функция contour, если ее вызвать с двумя входными аргументами (параметрами) C и h:
>> [C,h]=contour(X,Y,Z);
>> clabel(C,h)
Таким образом, если выполнить приведенные ниже команды, можно получить график, показанный на рис. 2.12.16.
Использование функции contourf в виде
>> contourf(X,Y,Z)
позволяет заполнить разными цветами промежутки между изолиниями (рис. 2.12.17), что может оказаться весьма удобным при визуализации результатов решения тестовых, модельных и практически важных задач.
Для построения изолиний в пространстве применяется функция contour3 (рис. 2.12.18).
>> contour3(X,Y,Z)
Задав четвертым входным аргументом функций contour и contour3 скалярное значение, можно указать количество уровней, для которых следует построить изолинии (по умолчанию количество уровней выбирается автоматически). Количество самих изолиний при этом может не совпадать с указанным количеством уровней, т.к. соответствующая плоскость может дать несколько разных линий пересечения с поверхностью.
Заметим, что среди многочисленных параметров функций contour, contourf и contour3, могут присутствовать пары типа
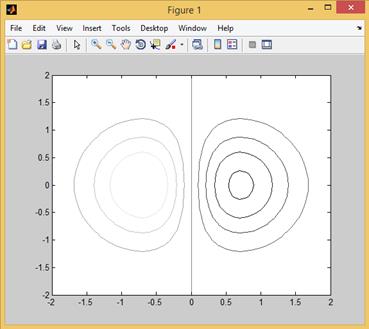
Рис. 2.12.15. Пример использования функции contour.
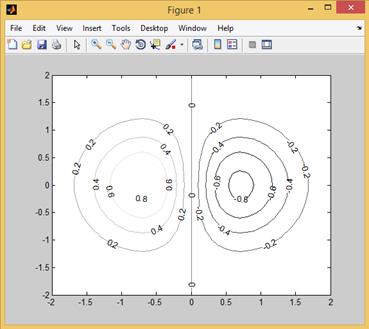
Рис. 2.12.16. Пример выполнения оцифровки изолиний.
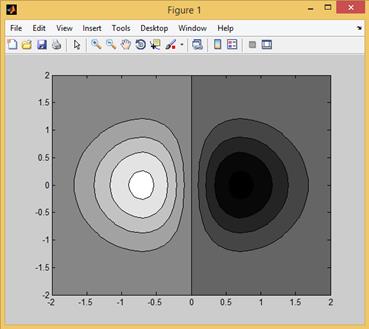
Рис. 2.12.17. Пример использования функции contourf.
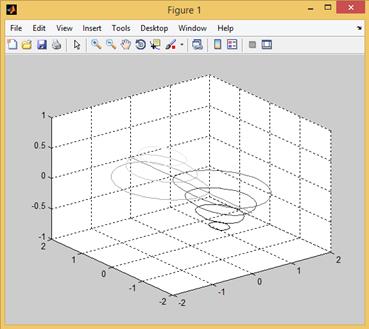
Рис. 2.12.18. Пример использования функции contour3.
('Свойство', значение)
инициализирующие значения соответствующих свойств.
Для изменения свойств изолиний можно воспользоваться массивом указателей, который возвращает функция contour3:
>> [X,Y]=meshgrid(-2:0.1:2);
>> Z=-2*X.*exp(-X.^2-Y.^2);
>> colormap(gray)
>> [C,h]=contour3(X,Y,Z,7);
>> set(h,'LineWidth',5)
Результат работы представленного фрагмента, в котором толщина изолиний была увеличена до 5 пунктов, приведен на рис. 2.12.19.
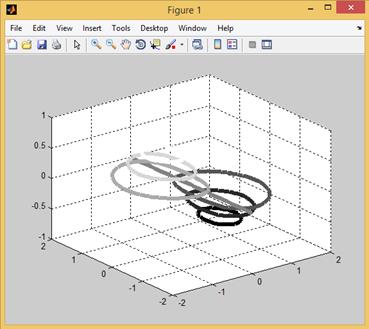
Рис. 2.12.19. Пример утолщенных пространственных изолиний.






