Объективность психодиагностики вообще и тестовых показателей в частности достигается путем неуклонного соблюдения психологом критериев достоверности психодиагностического измерения, а также путем приобретения опыта получения, использования и интерпретации полученных данных.
Достоверность психодиагностического измерения определяется валидностью (соответствием тестовых данных измеряемому свойству), надежностью (точностью психодиагностических измерений) и прогностичностью (предположением о развитии измеренного свойства) применяемых психологических методик (тестов).
Валидность тестов
Валидностью как элементом достоверности психодиагностического измерения свойств субъекта называется мера соответствия тестовых оценок представлениям о сущности свойств или их роли в той или иной деятельности человека. В теории психометрии определяют два основных типа и по крайней мере одиннадцать видов валидности методик (см. рис. 7).

Рис. 7. Структура валидности
Различают два типа валидности — внешнюю и внутреннюю*. Внешняя валидность есть мера возможности распространения результатов тестирования на генеральную совокупность**. Внешняя валидизация осуществляется путем расчета репрезентативности экспериментальной выборки при отработке теста и перекрестной валидизации, то есть определения валидности теста на выборке, отличающейся от той, на которой отрабатывался стимульный материал и задания к тесту.
* См.: Анастази А., Урбина С. Психологическое тестирование. — СПб., 2001.— С. 133-193.
** Там же.
Репрезентативность выборки — это представительность экспериментальной выборки, которая отражает основные свойства генеральной совокупности. Репрезентативность определяется путем сопоставления качественных и количественных характеристик экспериментальной выборки с характеристиками исследуемой популяции с целью определения их однородности.
К качественным характеристикам могут быть отнесены социально-демографические, видовые, интеллектуальные (образовательные), профессиональные и другие характеристики популяции (группы), которые являются предметом исследования или существенно влияют на него.
Количественная характеристика экспериментальной группы — это минимальная ее численность, сохраняющая свойства генеральной совокупности. Формирование репрезентативной выборки по количественному признаку осуществляется при помощи теоремы П. А. Чебышева о вероятности ошибки репрезентативности, которая гласит: «С вероятностью сколь угодно близкой к единице можно утверждать, что при достаточно большом числе независимых наблюдений выборочная средняя будет сколь угодно мало отличаться от генеральной средней» и далее (следствие 1 из теоремы П. А. Чебышева) «...что с вероятностью, как угодно близкой к единице («практически достоверно»), выборочная доля будет как угодно мало отличаться от генеральной доли, если объем выборки достаточно велик»*.
* Карасев А.И. Основы математической статистики. — М.: Росвузиздат, 1962. — С. 172.
В психологической литературе существует несколько теоретических подходов к расчету объема минимально репрезентативной выборки*. Часто приводятся таблицы опытно полученных данных**. Так, С. Москвин отмечает, что при объемах генеральной совокупности 400, 500, 1000, 2000, 5000, 10000 и более 10 тыс. человек минимальная выборка составляет соответственно 200, 222, 286, 333, 370, 398 и 400 испытуемых (указ. публ., с. 28). Г. Лоза указывает на следующее соотношение генеральной совокупности и объема экспериментальной выборки при проведении социологических исследований 100/16-17 чел., 300/50 чел., 1000/100 чел. и 5000/200 испытуемых. В лекции А. Гончарова минимальная репрезентативная выборка относительно генеральной совокупности соответственно составляет: 500/222, 1000/286, 2000/333, 3000/350, 4000/360, 5000/370, 10 000/385, 100 000/398 и более 100 000 - 400 респондентов.
* Введение в профессию. — М.: Воениздат, 1992; Карасев А.И. Основы математической статистики. — М.: Росвузиздат, 1962; Бурлачук Л.Ф., Морозов С.М. Словарь-справочник по психодиагностике. — СПб.: Питер-Ком, 1999 и др.
** Введение в профессию. — М.: Воениздат, 1992; Москвин С. Выборка в социологическом исследовании // Военно-социологическое исследование, 1993. С. 27-30; Гончаров А.И. Методы изучения общественного мнения и социальной информации (Лекция). - М.: ГА ВС, 1993.
В ходе анализа психологических данных для расчета объема минимальной репрезентативной выборки используются следующие формулы:
1) формула расчета объема минимальной репрезентативной выборки* при нахождении доли элементов генеральной совокупности, обладающих некоторым признаком (номинальная измерительная шкала):

* Карасев А.И. Основы математической статистики. — М.: Росвузиздат, 1962. — С. 213.
2) формула расчета объема минимальной репрезентативной выборки* при нахождении средней признака (интервальная измерительная шкала):

*Там же, с. 212.
3) формула расчета объема минимальной репрезентативной выборки*:

где n— объем минимальной репрезентативной выборки испытуемых;
t — коэффициент кратности ошибки, связанный с вероятностью гарантии ошибки выборочного наблюдения (величина t-критерия Стъюдента);
δ — величина стандартного отклонения;
D — размер ошибки доверительного интервала измерения признаков;
N — объем генеральной совокупности;
p — частота проявления данного признака;
q = 1 - р.
* Бурлачук Л.Ф., Морозов С.М. Словарь-справочник по психодиагностике. -СПб.: Питер-Ком, 1999. - С. 64-65.
Практическое задание. Рассчитать объем минимально-репрезентативной выборки испытуемых, если объем генеральной совокупности 5000 чел., а вероятность проявления исследуемого признака («угадывания» при помощи теста) — 0.8.
Дано: t — коэффициент кратности ошибки, связанный с вероятностью (Pt), с которой требуется гарантировать результаты выборочного наблюдения; D — размер ошибки доверительного интервала измерения признаков = 0,05; N — объем генеральной совокупности = 5000; р — частота проявления данного признака = 0.8; q = 1 — р = 0.2.
Определить: n — минимально необходимую численность экспериментальной выборки.
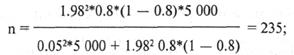
Ответ: n = 235.
Вывод: При повышении достоверности измерений происходит заметное уменьшение объема минимально репрезентативной выборки. Аналогичное влияние отказывает точность измерений (D).
Перекрестная валидизация производится путем апробации теста на выборке, отличной от экспериментальной. Перекрестная валидизация осуществляется для того, чтобы определить границы применения методики по критерию «характеристика популяции» (для определения уровня развития свойства у детей, подростков, мужчин-женщин, определенной группы специалистов и т. д.). В ходе перекрестной валидизации рассчитываются коэффициенты корреляции между одними и теми же показателями, полученными в результате тестирования разных групп испытуемых. Вывод о возможности применения теста на данной популяции делается при помощи параметрических критериев (t-критерий Стъюдента, n — критерий Уэлша).
Практическое задание. Рассчитать объем экспериментальной выборки по критерию обучаемости испытуемых (применялся тест ОСО*).
* ОСО — тест «Оценка общей способности к обучению».
Дано:
Группа 1 (школьники 9-го класса — 15 лет):
Количество испытуемых n = 471
Среднее значение показателя Мх = 3.75
Среднеквадратическое отклонение δ = 1.4
Группа 2 (школьники 10-го класса — 16 лет):
Количество испытуемых n =178
Среднее значение показателя Мх = 3.66
Среднеквадратическое отклонение δ = 0.8
Группа 3 (курсанты училища связи — 18 лет):
Количество испытуемых n=104
Среднее значение показателя Мх = 3.20
Среднеквадратическое отклонение δ=1.1
Решение: Для расчетов используется формула t-критерия:

* Экспериментальные выборки значимо не различаются на уровне р≤0.05.
** Экспериментальные выборки значимо различаются на уровне р≤0.05.
Вывод: в результате расчетов выявлено значимое различие показателей обучаемости между первой и третьей и между второй и третьей исследованными группами, которые не могут считаться однородными и составлять единую совокупность. Только между первой и второй выборками по данному критерию не существует значимых различий (р<0.05). В целях проверки валидности первую и вторую группы можно объединить в одну экспериментальную выборку и считать единой популяцией в количестве 649 человек.
Уяснив содержание внешней валидности методик, перейдем к рассмотрению аспектов внутренней валидности.
Внутренняя валидность — это мера соответствия тестовых оценок уровню развития измеряемого свойства. Она состоит по крайней мере из пяти элементов:
а) концептуальная (теоретическая) валидность — теоретическое обоснование возможности измерения исследуемого свойства данным психодиагностическим средством;
б) содержательная валидность — степень репрезентативности содержания заданий теста измеряемой области психических свойств;
в) конструктная валидность — степень репрезентативности исследуемого психологического конструкта в результатах теста («насколько результаты теста рассматриваются в качестве меры исследуемого психологического конструкта — фактора, свойства»)*
г) операционная валидность — степень репрезентативности в конкретных экспериментальных операциях реальных операциональных условий психической деятельности;
д) эмпирическая валидность — совокупность характеристик валидности теста, полученная сравнительным статистическим способом оценивания. К этим характеристикам относятся так называемые очевидная и критериальная виды валидности.
* Анастази А. Психологическое тестирование. В 2-х книгах. — М.: Педагогика. Т 1. С. 140.
Очевидная валидность — это представление о тесте, сфере его применения, результативности и прогностической ценности, которое возникает у испытуемого и другого лица, не располагающего специальными сведениями о характере использования и целях методики.
Критериальная валидность — комплекс характеристик, включающий текущую и прогностическую валидности методики и отражающий соответствие диагноза и прогноза определенному кругу критериев развития измеряемого свойства. Критериальная валидность оценивается величиной связи, корреляции показателя теста с «внешним критерием».
Эмпирическая валидность измеряется при помощи коэффициентов валидности.
Текущая [диагностическая (конкурентная)] валидность* мера способности теста дифференцировать испытуемых по изучаемому признаку. Текущая валидность теста определяется исходя из его «трудности» и мер изменчивости измеряемого признака.
* Текущая, диагностическая и конкурентная валидности здесь употребляются как синонимы.
Трудностью теста называется отношение количества решенных заданий методик к нерешенным заданиям*. Уровень трудности характеризуется коэффициентом трудности (Тт), который вычисляется по формулам А и Б.
* Анастази А. Психологическое тестирование. В 2-х книгах. — М.: Педагогика. Т. 1.С. 180-182.

где Np— количество решенных заданий теста; Nh — количество нерешенных заданий теста.
Оптимальная «трудность теста», рассчитанная с помощью формулы А, должна колебаться в пределах 50%, однако, как признают многие психологи, достичь такого положения крайне затруднительно. На практике критериальная «трудность» рассчитывается для всей тестовой батареи и уже ее значение должно колебаться в пределах 50%, а «трудность» входящих в нее тестов - находиться в пределах «умеренного разброса». Видимо, этот «умеренный разброс» находится в пределах d, то есть ± 16%. (Следует также учитывать 5%-ю ошибку вычислений.)

где δ — стандартное отклонение, которое вычисляется по формуле:
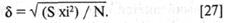
Трудность теста, рассчитанного по формуле (Б), находится в пределах от 1 до 25 (цифры 13 и 4 выбраны экспериментально в целях исключения отрицательных и дробных показателей и удобства расчетов). Средняя трудность теста имеет значение 13.
Практическое задание. Рассчитать трудность тестовой батареи, состоящей из двух субтестов.
Решение:

К мерам изменчивости измеряемых признаков, как правило, относят характеристики распределения эмпирических данных (нормальность распределения) и характеристики вариации признаков.
Нормальность распределения данных определяет численную характеристику дифференциации испытуемых. Она вычисляется при помощи критерия Хи-квадрат Пирсона, а также с использованием коэффициентов асимметрии и эксцесса распределения переменных.
Ширина полосы разброса данных по шкале измерений от min до max; это характеристика вариации признаков. Простейшими измерителями вариации признаков являются размах вариации R (это разность между наибольшим и наименьшим значениями признаков, то есть R = xmax — xmjn) и дискриминатив-ность заданий — субтестов (способность отдельных пунктов (заданий) теста дифференцировать обследуемых относительно «максимального» или «минимального» результата теста). Мера соответствия успешности выполнения одного субтеста всей методике является показателем дискриминативности заданий теста и называется коэффициентом дискриминации (индексом дискриминативности). Индекс дискриминативности теста рассчитывается в процессе разработки тестов и тестовой батареи. Он вычисляется при помощи а) точечно-биссериального коэффициента корреляции (Rpb) (см. выше) и б) метода контрастных групп в виде разности между долей лиц, правильно решивших задание из «высокопродуктивной» и «низкопродуктивной» групп (D)*.

* См. Словарь-справочник по психологической диагностике / Бурлачук Л.Ф., Морозов С.М. - Киев, 1989. - С. 47-48.
Наибольший интерес представляет характер группировки значений признака вокруг их средней. Мерой ее определения являются дисперсия (среднеквадратическое отклонение) и коэффициент вариации (V), который определяется как отношение дисперсии (dx) к среднему (Мх), выраженное в процентах:

Между характеристиками распределения и вариативностью переменных имеется связь, которая предопределяет оптимальное сочетание формы распределения с вариативностью. Большая вариативность признаков говорит о том, что распределение ненормально, асимметрично и сильно скошено. Малая вариативность показывает, что тест не дифференцирует испытуемых по измеряемому признаку (испытуемые отвечают или решают задание одинаково). При анализе трудности, нормальности распределения и вариативности показателей тестов необходимо соблюдать МЕРУ, которая вырабатывается в процессе накопления опыта диагностической работы и статистической обработки данных.
Прогностическая валидность является элементом содержания достоверности тестов и определяется как степень точности и обоснованности суждения о диагностируемом психическом свойстве по его результату спустя определенное время после измерения.
Показателем прогностичности теста является степень регрессии тестовых данных к объективным критериям. Регрессия представляет собой функцию f (х1 х2 х3,... хn), описывающую зависимость среднего показателя теста, измеряющего данное свойство от заданных фиксированных значений реального проявления этого свойства (внешнего критерия — у). Эта функция может носить линейный и нелинейный характер (линейная регрессия: у = b + ах; параболическая зависимость: у = b + ах + сх2; гиперболическая зависимость: у = b + а/х; показательная функция: у = b + а).
В практической психодиагностике для прогноза развития или проявления измеренного свойства чаще применяют линейную или множественную линейную регрессию (у = b + а1 х1 +а2 х2… +аn хn). Физический смысл ее заключается в приравнивании зависимой и независимой переменных. Изменение зависимой переменной прямо определяет изменение независимой переменной. Коэффициент а показывает угол наклона оси регрессии, а свободный член b — отстояние начала оси регрессии от начала координат. Коэффициент корреляции показывает уровень прогностичности функции, a R2 - уровень объясняемой дисперсии у за счет изменения х. При использовании тестовой батареи прогноз измеряемого свойства осуществляется посредством связанных между собой нескольких зависимых переменных (х1, x2, x3,... xn), которые и формируют множественную линейную регрессию. При использовании множественной линейной функции при прогнозе развития измеряемого свойства повышается уровень прогностичности тестирования и его достоверность за счет перекрытия разными методиками различных сторон измеряемого свойства.
Надежность тестов*
* См.: Анастази А., Урбина С. Психологическое тестирование. — СПб., 2001. — С. 103-132.
Надежность — это характеристика психодиагностической методики, отражающая точность психодиагностических измерений, а также устойчивость (стабильность) результатов теста к действию посторонних случайных факторов. Надежность и валидность являются важнейшими характеристиками методики как инструмента психологического исследования.
Наибольшая стабильность результатов наблюдается при применении графических и графологических тестов, показатели которых меняются крайне медленно. Медленно изменяется почерк, практически неизменными остаются качество линий рисунков и их композиция.
Наибольшая динамичность показателей наблюдается у интеллектуальных тестов, которые напрямую зависят от способности человека накапливать и перерабатывать информацию.
На устойчивость (стабильность) показателей теста влияют следующие факторы:
• состояние и настроение обследуемых;
• мотивация испытуемых к тестированию;
• эргономические факторы (освещенность, температура в помещении, вибрация, шумы и пр.);
• характеристика деятельности (монотонность-динамичность, помехи и др.);
• степень обучаемости (или натренированности) испытуемых и др.
Надежность результатов тестирования зависит также от а) изменчивости инструмента психологического измерения и б) факторов стабильности самой процедуры измерения. Таким образом, надежность есть степень согласованности результатов тестирования, получаемых при первом и последующих измерениях.
На практике наиболее широко применяются шесть типов надежности: надежность ретестовая (тест-ретест надежность); надежность параллельных форм; надежность частей теста (надежность как гомогенность тестов); надежность по Кудеру -Ричардсону; надежность интерпретатора («оценщика») и стандартная ошибка измерений.
Определение коэффициента надежности в первых двух случаях вычисляется по формулам расчетов коэффициентов корреляции (в зависимости от шкалы, в которой измерены данные) между первым и последующим измерениями или между параллельными формами теста.
Расчет коэффициента надежности при исследовании гомогенности теста осуществляется путем разбиения теста на равные субтесты и расчета корреляции между этими частями. Для определения общей надежности теста полученные коэффициенты корреляции вводятся в формулу Спирмена -Брауна:

где R — корреляция «половин» теста.
Если части теста являются отдельными дихотомическими заданиями, например вопросами, на которые может быть два ответа (да или нет), или заданиями с оценкой результата как правильного, так и неправильного, используется формула:

где рi— доля 1-го варианта ответа на i-й вопрос;
qi — доля 2-го варианта на i-й вопрос.
Надежность частей теста может также рассчитываться по формуле Кудера — Ричардсона:
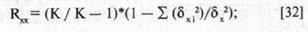
где К — количество равных частей теста;
δxi2 - дисперсия i-й части теста;
δх2 — дисперсия целого теста.
При работе с клиническими опросниками, тестами креативности и проективными технологиями надежность методик определяется путем сравнения интерпретаций результатов двумя или более экспертами-психологами. Высокие коэффициенты корреляции между ними показывают надежность тестовой оценки.
Коэффициенты надежности психологических измерений представляют собой величину дисперсии показателей, которая вычисляется путем возведения коэффициента корреляции в квадрат. Интерпретируется он следующим образом. Например, коэффициент корреляции между параллельными формами теста равен 0.75. Коэффициент надежности рассчитывается так: 0.752= 0.56. Это означает, что 56% дисперсии исследуемых тестовых данных зависят от истинной дисперсии признаков (данных параллельного теста), а 44% — от ошибок или случайных переменных.
Разберем гипотетический пример определения надежности двух форм теста* в ходе исследования креативности 100 школьников. В результате коэффициент надежности взаимозаменяемых форм с интервалом ретестирования две недели составил 0.7. Была вычислена надежность-гомогенность тестов при помощи формулы Спирмена — Брауна, которая составила 0.8. Надежность интерпретации («оценщика») с привлечением второго специалиста-психолога была равна 0.92. Анализ источников дисперсии ошибок показан в таблице.
* См. Анастази А., Урбина С. Психологическое тестирование. — СПб., 2001. — С. 120-121.
| Анализ источников дисперсии ошибок в исследуемом тесте | |
| По надежности взаимозаменяемых форм (с временным интервалом две недели) | 1 — 0.7 = 0.3 (ошибка ретеста + ошибка гомогенности) |
| По надежности эквивалентных половин теста (формула Спирмена — Брауна) | 1 — 0.8 = 0.2 (ошибка гомогенности) |
| Разность | 0.3 — 0.2 = 0. 1 (ошибка ретеста) |
| По надежности интерпретации («оценщика») | 1 — 0.92 = 0.08 (различия между интерпретациями) |
| Суммарная оценка дисперсии ошибок 0.2 + 0.1 + 0.08 = 0.38 | |
| Истинная дисперсия 1 — 0.38 = 0.62 |
Результаты исследования надежности теста креативности можно представить схематично в процентном распределении дисперсии показателей теста.
| «Истинная» дисперсия: 62% | Дисперсия ошибок: 38% | ||
| Временная устойчивость; согласованность форм; независимость от различий между интерпретациями («оценщиками»). | Ошибка гомогенности: 20% | Ошибка ретеста: 10% | Различия между интерпретациями; 8% |
Надежность теста можно выразить посредством расчета стандартной ошибки измерений — SEM (стандартная ошибка показателя)*. Она рассчитывается по формуле [33].
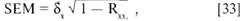
где δx — стандартное отклонение показателей теста;
Rxx — значение коэффициента надежности.
* См.: Анастази А., Урбина С. Психологическое тестирование. — СПб., 2001. — С. 127-131.
Физический смысл SEM заключается в определении дисперсии показателей конкретного теста вокруг «истинного показателя», которая характеризуется плотностью нормального распределения данных. Если, например, 68% всех случаев нормального распределения психологических данных попадает в интервал Мх ± δx, то примерно два шанса против одного (68: 32), что ошибка измерений будет «колебаться» в пределах ± 1 SEM. При увеличении плотности распределения данных, например –Мx± 3 SEM, увеличивается и вероятность предсказания (99.7:0.3) при соответствующем росте интервала ошибки в обе стороны.
Пример: рассчитаем стандартную ошибку измерений при помощи тестов CFIT и Равена. Интеркорреляция между показателями тестов составляет 0.81. Стандартное отклонение — 15. Результирующий показатель исследуемой методики CFIT равен, допустим, 110 IQ-баллов.

Это означает, что при определении «истинного» IQ и соотношении шансов удачного предсказания истины 2: 1 (или 68: 32) ошибка будет колебаться в интервале ±1.5 IQ-баллов. И «истинный» показатель теста находится в пределах от 103.5 до 116.5.
При увеличении вероятности прогноза до соотношения 99.7: 0.3 (3 ± δx) ошибка возрастает до ± 19.5, а «истинный» показатель займет место между 90.5 и 129.5.
Таким образом, надежность, валидность и прогностичность эмпирических данных дают возможность измерять психологические переменные на соответствующем уровне достоверности, который диктуется практикой социальных исследований.






