Задача №3. Расчет на прочность балки при изгибе

Дано: стальная балка на двух опорах, нагруженная системой внешних сил, лежащих в силовой плоскости, изображенной на рисунке 5.3, а. При расчетах принято: F= 20кН, m= 40кН∙м, q=100кН/м, [σ] = 160 МПа.

Требуется решить следующие задачи:

1. Определить опорные реакции балки;

2. Построить эпюры поперечных сил Q и изгибающих моментов М;

3. Из расчета на прочность подобрать сечение в форме стандартного профиля двутавровой прокатной балки.

Решение:

Определение опорных реакций (рисунок 5.3, б)

Представим балку как свободное тело, для чего отбросим опоры А и D, а их действие на балку заменим реакциями X_A, Y_A и Y_D.

Заменяем распределенную нагрузку .

При составлении уравнений равновесия примем для удобства правило знаков, по которому момент силы или момент пары сил, стремящийся повернуть балку вокруг моментной (неподвижной) точки в направлении вращения часовой стрелки, положительный.

Составим уравнения равновесия:

Откуда, получаем Y_D =108кН; Y_A≈212 кН; X_A=0.

Проверка. Правильность нахождения реакций опор можно оценить, например, составив уравнение суммы проекций всех сил на ось Y:

или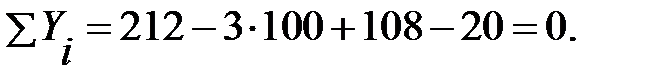

Следовательно, опорные реакции определены верно.

Построение эпюр поперечных сил Q и изгибающих моментов М для участков балки (рисунок 5.3, б).

1) Разбиваем балку на участки.

За границы участков принимаем сечения, где приложены момент М или сила F, а также границы действия распределенной нагрузки q. Направление обхода участков выбираются в зависимости от удобства вычислений, чем меньше нагрузок, тем проще формулы для вычислений. В данном случае имеем четыре участка (очередность буквенного обозначения определяет направление обхода, например, LD – начало обхода от точки L к D):

I – AB: 0≤ x1≤ 3м, (x1A=0; x1B=3м);

II – BC: 0≤ x2≤ 1м, (x2B=0; x2C=1м);

III – LD: 0≤ x3≤ 2м, (x3L=0; x3D=2м);

IV – DC: 0≤ x4≤ 2м, (x4D=0; x4C=2м).

Участок I. Выбираем начало координат в точке (опоре) А и приступаем к построению эпюр поперечных сил Q и изгибающих моментов М, применяя метод сечений.

Проводим сечение в пределах участка на расстоянии х1 от начала координат. Мысленно отбрасываем правую часть балки и рассматриваем равновесие оставшейся левой части. Составляем уравнения — сумму проекций всех сил на вертикальную ось и сумму моментов всех сил относительно рассматриваемого се­чения:

Задавая значения x₁, соответствующие границам участка I, по­лучим

Q_1A(x1=0) =Y_A=212кН; Q_1B(x1=3м) =Y_A-3q=-88кН;

M_1A(x1=0) =0кН∙м; M_1B (x1=3м) =3Y_A-32q/2=186 кН∙м.

Т.к. сила Q в пределах участка меняет знак, то, очевидно, имеется значение Q=0. Согласно дифференциальной зависимости , очевидно, что в точке пересечения (Q=0) изгибающий момент принимает экстремальное значение. Для нахождения этого экстремума вычисляем его координату по формуле:

Откуда, x ₁^Э=Y_A/q= 212/100=2,12 м.

Подставив значение x ₁^Э= 2,12 м в уравнение момента для участка, найдем величину экстремального момента

кН·м.

Участок II. Выбираем начало координат в точке В и приступаем к построению эпюр поперечных сил Q и изгибающих моментов М, применяя метод сечений.

Проводим сечение в пределах участка на расстоянии х₂ от начала координат. Мысленно отбрасываем правую часть балки и рассматриваем равновесие оставшейся левой части. Составляем уравнения — сумму проекций всех сил на вертикальную ось и сумму моментов всех сил относительно рассматриваемого сечения:

кН (не зависит от х₂);

.

Задавая значения x₂, соответствующие границам участка II, по­лучим значения изгибающего момента

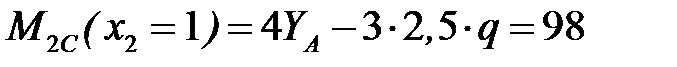кН·м;

кН·м.

Участок III. Выбираем начало координат в точке L и приступаем к построению эпюр поперечных сил Q и изгибающих моментов М, применяя метод сечений.

Проводим сечение в пределах участка на расстоянии x₃ от начала координат. Мысленно отбрасываем левую часть балки и рассматриваем равновесие оставшейся правой части. Составляем уравнения — сумму проекций всех сил на вертикальную ось и сумму моментов всех сил относительно рассматриваемого сечения:

кН (не зависит от х₃);

.

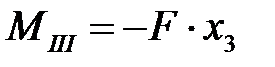Задавая значения x₃, соответствующие границам участка III, по­лучим значения изгибающего момента

;

кН·м.

Участок IV. Выбираем начало координат в точке D и приступаем к построению эпюр поперечных сил Q и изгибающих моментов М, применяя метод сечений.

Проводим сечение в пределах участка на расстоянии x₄ от начала координат. Мысленно отбрасываем левую часть балки и рассматриваем равновесие оставшейся правой части. Составляем уравнения — сумму проекций всех сил на вертикальную ось и сумму моментов всех сил относительно рассматриваемого сечения:

кН (не зависит от х₄);

Задавая значения x₄, соответствующие границам участка IV, получим значения изгибающего момента

кН·м.

кН·м.

По результатам проведенных расчетов строятся эпюры поперечных сил Q и изгибающих моментов M. Эти эпюры представлены на рисунках 5.3 в - г.

Определение сечения балки по условию прочности

Определим из расчета на прочность размеры поперечного сечения балки в форме двутавра.

Подбор сечения производится по максимальному изгибающему моменту M_max. Опасным является сечение в точке экстремума, где действует максимальный по абсолютному значению изгибающий момент M_max =225 кН·м.

Минимально допустимый момент сопротивления сечения изгибу равен

см³.

Стандартный профиль двутавра выбирается по ГОСТ 8239-89 (приложение С.5). Из таблицы сортамента выбираем двутавр № 50:

см³, площадь - A=100см².

 

Рисунок 5.3

№	F	m	q

Вопросы для письменного ответа

1. Какие внутренние силовые факторы возникают в поперечных сечениях балки при изгибе? Какое принято правило знаков при их определении?

2. Какие применяются основные правила проверки эпюр Q и M?

3. Что такое осевой момент инерции сечения и момент сопротивления сечения при изгибе?

4. Как записывается условие прочности балки при изгибе?

 

Варианты тестовых заданий

№	Задание	Ответы
5.1	Для заданной схемы нагружения балки укажите правильную эпюру поперечных сил.
5.2	Для заданной схемы нагружения балки укажите правильную эпюру изгибающих моментов.
5.3	Для заданной схемы нагружения балки укажите правильную эпюру изгибающих моментов.
5.4	Для заданной схемы нагружения балки укажите правильную эпюру поперечных сил.
5.5	Для заданной схемы нагружения балки укажите правильную эпюру изгибающих моментов.
5.6	Для заданной схемы нагружения балки укажите правильную эпюру изгибающих моментов.
5.7	Для заданной схемы нагружения балки укажите правильную эпюру поперечных сил.
5.8	Определить для заданной схемы нагружения изгибающий момент в опасном сечении балки длиной l.	M-q∙l2 M+q∙l2 M+q∙l2/6 M-q∙l2/2
5.9	Расположите номера точек в порядке возрастания нормальных напряжений при изгибе.	1. 4, 1, 2, 3 2. 2, 1, 3, 4 3. 2, 3, 4, 1 4. 4, 2, 3, 1

 

 

ПРИЛОЖЕНИЯ

ПРИЛОЖЕНИЯ

ПРИЛОЖЕНИЕ А

Оформление титульного листа контрольной работы

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ

ИНСТИТУТ СЕРВИСА

Кафедра Инженерных дисциплин