При расчете на изгиб, кручение и другие виды более сложного нагружения для оценки прочности и жесткости бруса недостаточно знать только площадь его поперечного сечения, требуется определять другие геометрические характеристики сечения: статический момент площади, осевые, центробежный и полярный моменты инерции.
Рассмотрим произвольную плоскую фигуру площадью A, отнесенную к системе координат zoy (Рисунок 3.1).
Обозначим: dA - площадь элементарной площадки; y, z - расстояние ее центра тяжести до осей координат.
Выражения вида
называются статическими моментами площади относительно осей y и z соответственно.
Зная величины статических моментов площади фигуры, можно вычислить координаты ее центра тяжести. Если заданное сечение можно разбить на части, для которых известны положения их центров тяжести и величины площадей, координаты центра тяжести всей фигуры определяются по формулам
| Рисунок 3.1 – Плоская фигура |
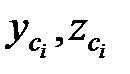- координаты центров тяжести этих элементов в выбранной системе координат y, z.
Центр тяжести лежит на оси симметрии сечения, а если таких осей несколько - в точке их пересечения.
Моментами инерции (осевыми моментами инерции) относительно осей y и z соответственно называются интегралы вида
Для простейших фигур и прокатных профилей величины моментов инерции приводятся в учебной и справочной литературе.
Выражение 
называется центробежным моментом инерции.
Оси, относительно которых центробежный момент инерции равен нулю, называются главными осями. Если хотя бы одна из выбранных координатных осей является осью симметрии, то обе эти оси будут главными. Осевые моменты инерции относительно главных центральных осей называются главными центральными моментами инерции. Они являются экстремальными по величине: один из них максимален, другой минимален.
Осевой момент инерции составного сечения вычисляется как сумма осевых моментов инерции отдельных составляющих фигур относительно одной и той же оси. При этом в таблицах сортамента прокатных профилей моменты инерции простых элементов определены относительно их собственных центральных осей, которые показываются на чертежах. Центральные оси составной фигуры обычно не совпадают с табличными. Тогда для вычисления моментов инерции подобных фигур приходится использовать зависимость между моментами инерции относительно параллельных осей:
где 
- моменты инерции сечения относительно произвольных осей; 
- моменты инерции сечения относительно центральных осей; A - площадь фигуры; a и в - расстояние между осями y, y0 и z, z0 соответственно.
Пример решения задачи
Дано: плоское сечение, представленное на рисунке 3.2.
Требуется найти:
Ø центр тяжести сечения;
Ø моменты инерции сечения относительно главных центральных осей;
Ø радиус инерции сечения относительно главной центральной оси ZC.
Решение:
Ось симметрии фигуры Y (рисунок 3.2) является главной осью инерции. Координата zC=0, т.к. центр тяжести лежит на оси симметрии Y=YC.
Определим положение центра тяжести фигуры по оси симметрии Y.
Разобьем сложную фигуру на составляющие простые: два равнобедренных треугольника I, III и прямоугольник II (Рисунок 3.2). Площади выделенных фигур:
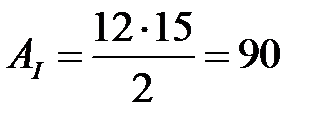см2; 
см2; 
см2,
всей фигуры - 
см2.
Расчеты удобно свести в таблицу:
| № фигуры | Ai | yi | SZi |
| см2 | см | см3 | |
| 1 | 90 | 12 | 1080 |
| 2 | 600 | 0 | 0 |
| 3 | -36 | -8 | 288 |
| A=654см2 | SZ=1368см3 |
| Рисунок 3.2 |
Для определения статического момента введем вспомогательную ось Z, проходящую через центр тяжести прямоугольника II. В этом случае статический момент фигуры II равен нулю. Чтобы найти статические моменты треугольников, умножаем площадь выделенных фигур на координаты их центра тяжести в системе YZ:
Тогда 
см.
Откладываем эту координату и проводим через центр тяжести (точку С на рисунке 3.3) главную центральную ось ZC.
Найдем моменты инерции всей фигуры относительно главной центральной оси ZC, складывая (или вычитая) моменты инерции составляющих фигур:
Для этого определим моменты инерции каждой из фигур I, II, III относительно горизонтальной оси - собственной главной центральной оси ZCi // ZC, используя табличные формулы (см. приложение С3)
Рисунок 3.3
для равнобедренного треугольника I
см4;
для прямоугольника II
см4;
для равнобедренного треугольника III
см4;
По формулам параллельного переноса осей 
, где yiС – расстояние от центра тяжести i- ой фигуры Сi до центра тяжести всего сечения С, определяем главный центральный момент инерции сечения
см4.
Радиус инерции относительно главной центральной оси ZC определяется по формуле
см.
Вопросы и задания для самоконтроля
6. Для чего необходимы геометрические характеристики плоских сечений?
7. Назовите основные геометрические характеристики поперечных сечений.
8. Что такое статический момент плоской фигуры? Какова его размерность?
9. Какими свойствами обладает статический момент?
10. Как определяется положение центра тяжести сечения?
11. Что такое момент сопротивления сечения?
12. Какие оси называются центральными осями?
13. Какие оси и какие моменты инерции называются главными?
Варианты тестовых заданий
| 3.1 | Определить положение центра тяжести сечения относительно координатных осей | |
| 3.2 | Определить статический момент сечения относительно оси Y | |
| 3.3 | Определить статический момент сечения относительно оси Z | |
| 3.4 | Определить момент инерции сечения относительно оси Y. | |
| 3.4 | Определить момент инерции сечения относительно оси Y, если известен его момент инерции относительно центральной оси Yс - Jyc=d4 и площадь A = 3d2/2. | |
| 3.6 | Определить положение центра тяжести сечения относительно оси Y | |
| 3.7 | Определить h прямоугольного сечения, если известен момент сопротивления Wy=144 см3 при изгибе и соотношение h/b=2. |
