При растяжении (сжатии) в поперечных сечениях бруса возникают только продольные силы, направленные вдоль его оси, все остальные внутренние усилия равны нулю.
1. Определение продольной силы.
Продольная или нормальная сила N считается положительной при растяжении и отрицательной при сжатии. Ее величина может быть найдена с помощью метода сечений (РОЗУ), как алгебраическая сумма проекций на ось бруса всех внешних сил, приложенных к брусу по одну сторону от рассматриваемого сечения:
 ,
,
где Fi – сосредоточенные силы; qx – распределенная нагрузка по одну сторону от рассматриваемого сечения.
Эпюра продольной силы N представляет собой график ее изменения вдоль геометрической оси стержня.
2. Определение нормальных напряжений.
Действующая в поперечном сечении продольная сила N равномерно распределяется по всему сечению и, как следствие этого, нормальные напряжения σ также равномерно распределяются по всему сечению.
Их величина определяется по формуле:
 ,
,
где Ni - продольная сила в i-ом поперечном сечении; Аi - его площадь.
В системе СИ сила выражается в ньютонах (Н), площадь поперечного сечения - в мм2, нормальное напряжение - в МПа (1МПа = 1Н/мм2).
Эпюра σ строится аналогично эпюре N, но в своем масштабе.
3. Определение перемещений в стержневых и шарнирно- стержневых системах.
Линейные упругие перемещения в системах растяжения (сжатия) возникают в результате удлинения (или укорочения) стержней, определяемого по формулам, вытекающим из физического закона Гука:

где l - длина бруса; E - коэффициент пропорциональности (модуль упругости первого рода, или модуль Юнга). Модуль Юнга - это физическая характеристика материала, измеряемая в МПа.
Для бруса с несколькими расчетными участками (т.е. в пределах которых N, E, А постоянны) удлинение подсчитывается как алгебраическая сумма их удлинений:
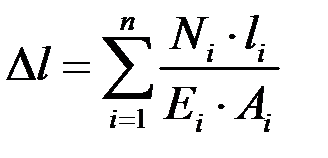 .
.
В шарнирно – стержневых системах перемещения шарниров определяется методом засечек (рисунок 2.2). Суть метода состоит в следующем:
а) мысленно разъединяют стержни и отмечают на схеме удлинения или укорочения стержней;
б) стержни вращают вокруг точек подвеса до встречи, из-за малости упругих перемещений вращение осуществляется не по дуге, а по касательной, т.е. по перпендикулярно радиусу вращения.

Рисунок 2.2- Метод засечек
В сложных статистически определимых и во всех статистически неопределимых системах используется обратный метод засечек (рисунок 2.3):
а) задаются конечным положением жесткого элемента или положением шарнира после деформации;
б) из этого положения восстанавливают перпендикуляры на продолжение деформируемых стержней, отсекающих их удлинение или укорочение.
По результатам построений в прямом и обратном методе засечек ищут геометрическую связь между положениями шарниров и абсолютной деформацией стержней.
4. Использование условия прочности.
Соотношение smax £ [s], называется условием прочности по допускаемым напряжениям. Здесь [s] - допускаемое напряжение материала бруса.
Допускаемое напряжение [ s ] либо задается заранее, либо находится по формуле:
 ,
,
где s op = sт - предел текучести для пластичных материалов; s op = sт - временное сопротивление (предел прочности) для хрупких материалов; nσ - запас прочности материала, величина которого имеет статистический характер и связана с конструктивными особенностями, условиями эксплуатации и риском разрушения конкретного изделия.

Рисунок 2.3.- Обратный метод засечек
С помощью условия прочности можно решать три основных задачи сопротивления материалов.
1. Подобрать сечение растянутого (сжатого) бруса, при котором его прочность будет обеспечена.
Необходимая площадь поперечного сечения растянутого (сжатого) бруса определяется в виде

Зная форму сечения и его площадь, можно определить линейные размеры сечения или по сортаменту подобрать требуемый стандартный профиль: уголок, швеллер, двутавр и т.п.
2. Определить допускаемую нагрузку, если известны прочностные свойства материала и площадь поперечного сечения бруса:
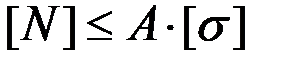 .
.
Это соотношение позволяет вычислить наибольшее значение продольной силы N, действующей в опасном сечении и, следовательно, величину допускаемых внешних нагрузок, приложенных к брусу.
3. Провести поверочный расчет прочности бруса.
При поверочном расчете нагрузки, размеры и материал, из которого изготовлен брус, считаются известными. Вычисляется наибольшее нормальное напряжение в опасном поперечном сечении и сравнивается с допускаемым напряжением:
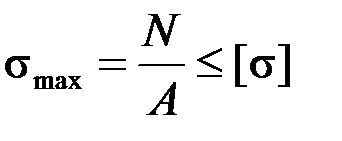 .
.
Если данное условие выполняется, то прочность бруса обеспечена.
Пример решения задачи 1.1






