Пусть функция  непрерывна на отрезке
непрерывна на отрезке 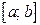 . Как известно, такая функция достигает своих наибольшего и наименьшего значений. Эти значения функция может принять либо во внутренней точке
. Как известно, такая функция достигает своих наибольшего и наименьшего значений. Эти значения функция может принять либо во внутренней точке  отрезка
отрезка 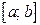 , либо на границе отрезка, т.е. при
, либо на границе отрезка, т.е. при 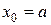 или
или 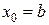 . Если
. Если 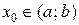 , то точку
, то точку  следует искать среди критических точек данной функции.
следует искать среди критических точек данной функции.
Наибольшее значение функции  на
на 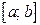 называется абсолютным максимумом, а наименьшее – абсолютным минимумом.
называется абсолютным максимумом, а наименьшее – абсолютным минимумом.
Правило нахождения наибольшего и наименьшего значения функции на 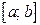 :
:
1) найти критические точки функции на интервале  ;
;
2) вычислить значения функции в найденных критических точках;
3) вычислить значения функции на концах отрезка, т.е. в точках  и
и 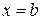 ;
;
4) среди всех вычисленных значений функции выбрать наибольшее и наименьшее.
Пример 16.22. Найти наибольшее и наименьшее значения функции  на отрезке
на отрезке  .
.
Решение. Находим критические точки данной функции:
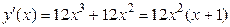 ;
;
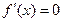 при
при 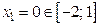 и при
и при  . Находим:
. Находим:
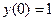 ;
;
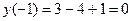 ;
;
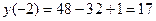 ;
;
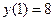 .
.
Итак, 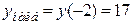 в точке
в точке 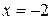 ,
, 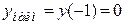 в точке
в точке 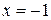 .
.
,
Если промежуток открытый, функция принимает наибольшее и наименьшее значения только в точках экстремума.
Нахождение наибольшего и наименьшего значений функции широко применяется при решении многих практических задач математики, физики, химии, экономики и других дисциплин. В прикладных задачах чаще всего встречается простой случай, когда между a и b находится только одна критическая точка  (промежуток может быть и открытым, и бесконечным). Если в этой точке функция имеет максимум (минимум), то в этой точке будет и наибольшее (наименьшее) значение функции на промежутке.
(промежуток может быть и открытым, и бесконечным). Если в этой точке функция имеет максимум (минимум), то в этой точке будет и наибольшее (наименьшее) значение функции на промежутке.
Практические задачи: транспортная задача о перевозке груза с минимальными зат-ратами, задача об организации производственного процесса с целью получения макси-мальной прибыли и другие задачи, связанные с поиском оптимального решения, приводят к развитию и усовершенствованию методов отыскания наибольшего и наименьшего зна-чений. Решением таких задач занимается особая ветвь математики – линейное програм-мирование.
Пример 16.23. Из шара радиуса R выточить цилиндр наибольшего объема. Каковы его размеры?
Решение. Обозначим через x и y высоту и диаметр цилиндра.

Находим наибольшее значение функции 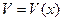 на промежутке
на промежутке 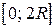 .
.
Так как  , то
, то 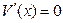 при
при 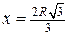 . Кроме того,
. Кроме того,  . Поэтому
. Поэтому 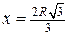 – точка максимума. Так как функция имеет одну критическую точку, то цилиндр будет иметь наибольший объем (равный
– точка максимума. Так как функция имеет одну критическую точку, то цилиндр будет иметь наибольший объем (равный  ) при
) при 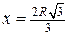 ; диаметр основания цилиндра равен
; диаметр основания цилиндра равен
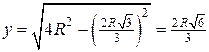 .
.
Таким образом, искомый цилиндр имеет высоту, равную 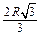 , и диаметр, равный
, и диаметр, равный  .
.
,
Выпуклость и вогнутость графика функции.
Точки перегиба
График дифференцируемой функции  называется выпуклым на интервале
называется выпуклым на интервале  , если он расположен ниже любой своей касательной, т.е.
, если он расположен ниже любой своей касательной, т.е.  , и вогнутым, если он расположен выше касательной, т.е.
, и вогнутым, если он расположен выше касательной, т.е. 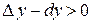 .
.
Определение 16.4. Точки график, в которых выпуклость сменяется вогнутостью или наоборот, называются точками перегиба графика.
Интервалы выпуклости и вогнутости находятся с помощью следующей теоремы, которую примем без доказательства.
Теорема 16.16. Пусть функция  определена и дважды дифференцируема на
определена и дважды дифференцируема на  , т.е. существует
, т.е. существует 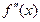 . Тогда если
. Тогда если 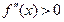 на
на  , то на этом промежутке график вогнутый, если
, то на этом промежутке график вогнутый, если 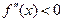 , то график выпуклый.
, то график выпуклый.
Сформулируем необходимое и достаточное условие точки перегиба в виде теорем, которые примем без доказательства.
Теорема 16.17. (необходимое условие точки перегиба) Пусть дана функция  , дважды дифференцируемая на X. Если в точке
, дважды дифференцируемая на X. Если в точке 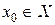 график этой функции имеет перегиб и существует конечная вторая производная
график этой функции имеет перегиб и существует конечная вторая производная  , то
, то 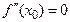 .
.
Теорема 16.18. (достаточное условие точки перегиба) Если функция  дважды непрерывно дифференцируема на X и при переходе через точку
дважды непрерывно дифференцируема на X и при переходе через точку  производная
производная 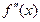 меняет знак, то точка
меняет знак, то точка  является точкой перегиба функции
является точкой перегиба функции 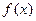 .
.
Пример 16.24. Найти интервалы выпуклости и вогнутости и точки перегиба, графика функции:
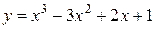 .
.
Решение. Функция определена на 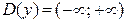 . Находим:
. Находим:
 ;
;
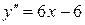 .
.
Из условия 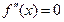 имеем:
имеем: 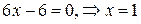 . Критической точкой будет
. Критической точкой будет 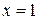 . Исследуем знак второй производной
. Исследуем знак второй производной  вблизи этой точки.
вблизи этой точки.
При 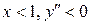 , а при
, а при 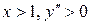 . Следовательно, на интервал
. Следовательно, на интервал 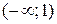 график выпуклый, на
график выпуклый, на 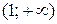 – вогнутый, а в точке
– вогнутый, а в точке 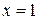 имеет перегиб.,
имеет перегиб.,
Асимптоты графика функции
Определение 16.5. Прямая L называется асимптотой кривой, заданной уравне-нием  , если расстояние между точками кривой и прямой стремится к нулю с удалением точки на кривой от начала координат.
, если расстояние между точками кривой и прямой стремится к нулю с удалением точки на кривой от начала координат.
Асимптоты могут быть вертикальными, наклонными и горизонтальными.
Вертикальная асимптота
Прямая  является вертикальной асимптотой, если точка
является вертикальной асимптотой, если точка  – есть точка разрыва второго рода функции
– есть точка разрыва второго рода функции  , т.е. если хотя бы один из односторонних пределов
, т.е. если хотя бы один из односторонних пределов  равен бесконечности.
равен бесконечности.




