Производная  функции
функции 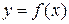 есть также функция от x и называется производной первого порядка.
есть также функция от x и называется производной первого порядка.
Если функция  дифференцируема, то ее производная называется производ-ной второго порядка и обозначается:
дифференцируема, то ее производная называется производ-ной второго порядка и обозначается:  или
или  . Итак,
. Итак,
 .
.
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается:  или
или 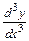 . Итак,
. Итак,
 .
.
Производная n -го порядка (или n -й производной) называется производная от производной 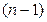 порядка:
порядка:
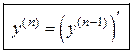 . (16.7.)
. (16.7.)
Производная порядка выше первого называются производными высших порядков. Начиная с производной четвертого порядка, производные обозначаются римскими цифрами или числами в скобках, например,  или
или  – производная пятого порядка.
– производная пятого порядка.
Пример 16.10. Найти значение производной 4-го порядка для функции  при
при  .
.
Решение. Находим последовательно
 ;
;
 ;
;
 ;
;
 .
.
Следовательно,  .,
.,
Пример 16.11. Найти производную n -го порядка для функции  .
.
Решение. Находим последовательно
 ;
;
 ;
;
 ;
;
 ;
;
…………………….
 .
.
,
Отметим, что в формуле (16.7.) принято  , т.е. производная нуле-вого порядка есть сама функция.
, т.е. производная нуле-вого порядка есть сама функция.
Пусть материальная точка движется прямолинейно по закону  . Как известно, производная первого порядка
. Как известно, производная первого порядка  .
.
Механический смысл производной второго порядка: вторая производная от пути по времени есть величина ускорения прямолинейного движения материальной точки, т.е.  .
.
Пусть функция 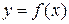 задана неявно в виде уравнения
задана неявно в виде уравнения  .
.
Продифференцировав это уравнение по x и разрешив полученное уравнение отно-сительно  , найдем производную первого порядка. Продифференцировав по x первую производную, получим вторую производную от неявной функции. В нее войдут x, y и
, найдем производную первого порядка. Продифференцировав по x первую производную, получим вторую производную от неявной функции. В нее войдут x, y и  . Подставляя уже найденное значение
. Подставляя уже найденное значение  в выражение второй производной, выразим
в выражение второй производной, выразим  через x и y.
через x и y.
Аналогично поступаем для нахождения производной третьего (и выше) порядка.
Пример 16.12. Найти производную второго порядка функции, заданной уравне-нием  в точке
в точке  .
.
Решение. Находим производную первого порядка:
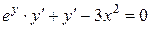 Þ
Þ  .
.
Используя равенство 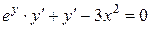 , дифференцируем обе его части, считая y функцией по x. Получаем
, дифференцируем обе его части, считая y функцией по x. Получаем
 ;
;
 .
.
Отсюда
 .
.
Следовательно,  .
.
,
Пусть функция 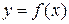 задана параметрическими уравнениями
задана параметрическими уравнениями
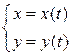 .
.
Как известно, первая производная  находится по формуле
находится по формуле  .
.
Найдем вторую производную от функции, заданной параметрически.
Из определения второй производной и равенства (16.6.) следует, что
 ,
,
т.е.
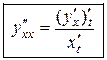 . (16.8.)
. (16.8.)
Эту формулу можно преобразовать и получить следующую формулу
 .
.
Итак,
 . (16.9.)
. (16.9.)
Аналогично получаем
 ,
,  , и т.д.
, и т.д.
Пример 16.13 Найти вторую производную функции
 .
.
Решение. Находим производные  и
и 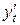 :
:
 ;
;
 .
.
Далее
 .
.
Используя формулу (16.8.), получаем
 .,
.,
Дифференциал функции
Пусть дана функция 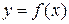 , определенная на множестве X, и в точке
, определенная на множестве X, и в точке  имеет отличную от нуля производную, т.е.
имеет отличную от нуля производную, т.е.  . Тогда по теореме о связи функции, ее предела и б.м.ф., можно записать
. Тогда по теореме о связи функции, ее предела и б.м.ф., можно записать  , где
, где 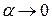 при
при 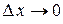 , или
, или 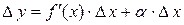 .
.
Таким образом, приращение функции 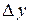 представляет собой сумму двух сла-гаемых
представляет собой сумму двух сла-гаемых  и
и 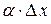 , являющиеся бесконечно малыми при
, являющиеся бесконечно малыми при 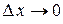 . При этом первое слагаемое есть бесконечно малая функция одного порядка с
. При этом первое слагаемое есть бесконечно малая функция одного порядка с  , так как
, так как  , а второе слагаемое есть бесконечно малая функция более высо-кого порядка, чем
, а второе слагаемое есть бесконечно малая функция более высо-кого порядка, чем  , так как
, так как 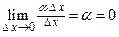 .
.
Слагаемой  называют главной частью приращения функции
называют главной частью приращения функции 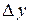 .
.
Определение 16.2. Дифференциалом функции 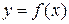 в точке x называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается
в точке x называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается 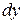 (или
(или  ):
):
 . (16.10.)
. (16.10.)
Дифференциал 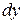 называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной x, т.е. дифференциал функции
называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной x, т.е. дифференциал функции  . Так как
. Так как  , то согласно формуле (16.10.), имеем
, то согласно формуле (16.10.), имеем  , т.е. дифференциал независимой переменной равен приращению этой переменной:
, т.е. дифференциал независимой переменной равен приращению этой переменной:  . Поэтому формулу (16.10.) можно записать так:
. Поэтому формулу (16.10.) можно записать так:
 , (16.11.)
, (16.11.)
иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Из формулы (16.11.) следует равенство  . Теперь обозначение производной можно рассматривать как отношение дифференциалов
. Теперь обозначение производной можно рассматривать как отношение дифференциалов 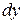 и
и  .
.
Пример 16.14. Найти дифференциал функции
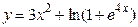
а) в общем виде;
б) в точке 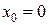 ;
;
в) при 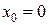 и
и  .
.
Решение. Находим производную первого порядка:
 .
.
а) Используя формулу (16.11.), получаем
 .
.
б) Дифференциал функции в точке равен
 .
.
в) При 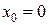 и
и  получаем:
получаем:
 .
.
,
Выясним геометрический смысл дифференциала функции.

Проведем к графику функции 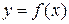 в точке
в точке  касательную
касательную 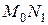 и рассмотрим ординату этой касательной для точки
и рассмотрим ординату этой касательной для точки  . На рисунке
. На рисунке  ,
,  . Из прямоугольного треугольника
. Из прямоугольного треугольника  имеем:
имеем:
 , т.е.
, т.е.  .
.
Но, согласно геометрическому смыслу производной,  . Поэтому
. Поэтому  .
.
Сравнивая полученный результат с формулой (16.10.), получаем  .
.
Геометрический смысл: дифференциал функции 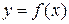 в точке x равен приращению ординаты касательной к графику функции в этой точке, когда x получит приращение
в точке x равен приращению ординаты касательной к графику функции в этой точке, когда x получит приращение  .
.
Правила вычисления дифференциала аналогичны соответствующим правилам нахождения производной.
Инвариантность формы записи дифференциала
Пусть 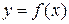 для
для  , тогда
, тогда
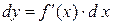 .
.
Рассмотрим сложную функцию  , где
, где 
 , причем
, причем  и
и 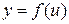 дифференцируемы соответственно в точках x и
дифференцируемы соответственно в точках x и  . Тогда
. Тогда  , но
, но  следовательно,
следовательно,  . А так как
. А так как  , то
, то
 .
.
Таким образом, форма записи дифференциала сохраняется, если независимую переменную заменить некоторой функцией. Это свойство называется инвариант-ностью (неизменностью) формы записи дифференциала.
Заметим, что из инвариантности следует, что, хотя  (x – незави-симая переменная), а
(x – незави-симая переменная), а  (
(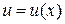 – функция), запись их одинакова. Однако сущность этих формул различна:
– функция), запись их одинакова. Однако сущность этих формул различна:  задается произвольно,
задается произвольно,  же задавать произвольно, вообще говоря, нельзя;
же задавать произвольно, вообще говоря, нельзя;  нужно вычислить по формуле дифференциала
нужно вычислить по формуле дифференциала  . Это относится и к случаю с несколькими промежуточными функциями.
. Это относится и к случаю с несколькими промежуточными функциями.






