Ниже мы увидим, что знание первой производной или производной более высокого порядка позволяет дать заключение о поведении функции. Но предварительно рассмотрим несколько основных теорем дифференциального исчисления.
Теорема 16.6. (Ферма) Пусть функция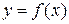 
определена на интервале 
и во внутренней точке 
этого интервала принимает наибольшее или наимень-шее значение. Если существует конечная производная 
, то 
.
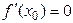Доказательство. Пусть 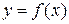в точке 
принимает наибольшее значение, т.е. 
для 
. По определению производной
.
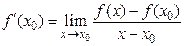Этот предел не зависит от того, приближается x к слева или справа.
Разность 
, следовательно, при 
,
а при 
.
Переходим к пределу:
, 
.
Так как по условию существует, то односторонние производные равны и .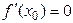
,
В доказательстве теоремы существенно, что - внутренняя точка интервала , так как мы рассматриваем точки справа и слева от . Если совпадает с концом промежутка, то производная может быть и не равна нулю. Например, функция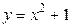 
на отрезке 
, а не на интервале 
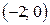, наибольшее значение достигает при 
. Однако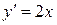 
. Тогда 
.
Теорема 16.7. (Ролля) Пусть задана функция 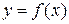и пусть она:
1) определена и непрерывна на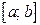 
;
2) дифференцируема на интервале ;
3) имеет равные значения на концах отрезка, т.е.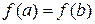 
.
Тогда найдется хотя бы одна точка 
, что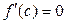 
.
Доказательство. Пусть 
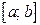непрерывна на , следовательно, достигает наибольшего M и наименьшего m значений, т.е. 
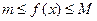. Рассмотрим два случая.
1. 
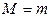. Тогда 
, 
, 
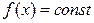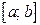, и любую точка из можно принять за c.
2. 
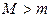. Так как 
, то M и m не достигаются оба на концах отрезка, т.е. хотя бы одно достигается в точке 
. А по теореме Ферма .
,
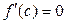Все условия теоремы Роля существенны. Если хотя бы одно из них не выполняется, то теорема тоже не будет выполняться. Например, для функции 
на отрезке 
условия 1 и 3 выполняются. На отрезке функция определена и непрерывна (первое условие), 
(третье условие). Но в точке 
функция не дифференцируема. Значит, теорема Ролля не выполняется.
Теорема 16.8. (Коши) Пусть заданы функции 
и 
и пусть:
1) они обе определены и непрерывны на ;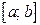
2) существуют 
и 
на ;
3) 
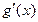на .
Тогда найдется такая точка , что выполняется равенство
.
Доказательство. Очевидно, что 
. Так как если бы 
, функция удовлетворяла бы теореме Ролля и нашлась бы точка c между a и b, такая, что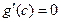 
, а это противоречит условию на .
Введем вспомогательную функцию
.
Она удовлетворяет условиям теоремы Ролля. Действительно,
1) 
определена и непрерывна на ;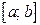
2) 
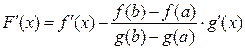существует на ;
3) 
.
Следовательно, существует точка , такая, что 
. Действитель-но,
или
,
т.е.
.
,
Теорема 16.9. (Лагранжа) Пусть заданы функции 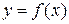и пусть она:
1) определены и непрерывны на ;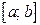
2) имеет конечную производную на .
Тогда найдется такая точка , что выполняется равенство
.
Доказательство. Теорему Лагранжа можно рассматривать как частный случай теоремы Коши. Действительно, положив 
, находим 
.
Подставляя эти значения в формулу , получаем или 
.
,
Формулу еще называют формулой Лагранжа или формулой о конечном приращении: приращение дифференцируемой функции на отрезке 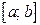равно приращению аргумента, умноженному на значение производной функции в некоторой внутренней точке этого отрезка.
Теоремы Ролля, Коши и Лагранжа называются теоремами о средних значениях. Это значит, что для каждого отрезка существует по крайней мере внутренняя точка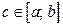 
(не обязательно в середине отрезка!), для которой эти теоремы выполняются.
Правило Лопиталя
Во многих случаях отыскание предела функции в точке или на бесконечности приводит к неопределенностям вида 
, 
, 
, 
, 
, 
, 
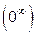, для раскрытия которых можно использовать понятие производной. Введем правило Лопиталя.
Теорема 16.10. (Правило Лопиталя раскрытия неопределенности 
)
Пусть функции и непрерывны и дифференцируемые в окрестности точки . Пусть 
и в указанной окрестности и 
, 
. Тогда, если существует 
(конечный или бесконечный), то существует 
и имеет место равенство
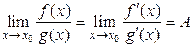. (16.15.)
Доказательство. Доопределим функции и в точке , полагая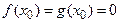 
. Тогда они будут непрерывны в точке . Применим к ним теорему Коши на отрезке 
и получим
,
где точка c удовлетворяет условию 
или 
. Если 
, то 
поэтому, согласно условию теоремы,
.
,
Коротко полученную формулу читают так: предел отношения двух бесконечно малых равен пределу отношения их производных, если последний существует.
Замечания. 1) Теорема 16.10. справедлива и в том случае, когда 
. Действи-тельно, положив 
, получим
.
2) Если производные и 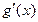удовлетворяют тем же условиям, что и функции и теорему 16.10. можно применить еще раз:
и т.д.
Пример 16.17. Найти 
.
Решение. 
.
,
Теорема 16.10. дает возможность раскрыть неопределенность вида . Сформу-лируем без доказательства теорему о раскрытии неопределенности вида .
Теорема 16.11. (Правило Лопиталя раскрытия неопределенности 
)
Пусть функции и непрерывны и дифференцируемые в окрестности точки (кроме, может быть, точки ), в этой окрестности 
, 
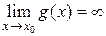, и . Тогда, если существует (конечный или бесконечный), то существует и имеет место равенство
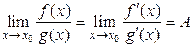. (16.16.)
Пример 16.18. Найти 
.
Решение. Способ 1.
Способ 2.
.
,
Пример 16.19. Найти 
.
Решение.
.
,
