Процессы, происходящие в механике, физике, химии, термодинамике, экономике, очень часто описываются функциями, заданными формулами. Чтобы знать характерис-тики рассматриваемого процесса, следует изучить характеристики функций, описы-вающих процесс, а для наглядности рассмотреть функции в их графическом задании. Но чаще интерес представляет не графическое задание функции, а качественное поведение графика функции без соблюдения масштабных размеров для достаточно точного (прибли-женного с заданной точностью) определения значений функции. Эти качественные свойства функций можно описать, используя методы дифференциального исчисления.
Теорема 16.12. (условие монотонности функции) Пусть функция  определена на X и внутри имеет конечную производную
определена на X и внутри имеет конечную производную  . Для того чтобы
. Для того чтобы 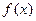 была монотонно возрастающей (убывающей), достаточно, чтобы
была монотонно возрастающей (убывающей), достаточно, чтобы  (
( ) для всех x внутри X.
) для всех x внутри X.
Доказательство. Возьмем промежуток 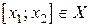 так, чтобы
так, чтобы  , и применим к функции
, и применим к функции 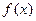 на этом промежутке формулу Лагранжа:
на этом промежутке формулу Лагранжа:
 ,
,
где  .
.
Если  и
и 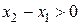 , то
, то  . Следовательно, функция возрастает.
. Следовательно, функция возрастает.
Если  и
и 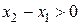 , то
, то  . Следовательно, функция убывает.
. Следовательно, функция убывает.
,
Если функция 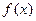 , определенная и непрерывная на множестве X, не является монотонной, то найдутся такие части промежутка X, что наибольшее или наименьшее значение достигается функцией во внутренней точке.
, определенная и непрерывная на множестве X, не является монотонной, то найдутся такие части промежутка X, что наибольшее или наименьшее значение достигается функцией во внутренней точке.
Определение 16.3. Функция  имеет в точке
имеет в точке  максимум (минимум), если существует такая окрестность точки
максимум (минимум), если существует такая окрестность точки 
 , не выходящая из области определения функции, что для всех
, не выходящая из области определения функции, что для всех 

 .
.
Максимум и минимум называют общим термином «экстремум».
Из определения экстремума следует, что вне окрестности точки максимума  значения функции могут быть больше этого максимума. Поэтому такой максимум назы-вается локальным (местным). Аналогично определяется локальный минимум. Точки локального максимума и минимума называются точками локального экстремума, а значе-ния функции в них – локальными экстремумами функции.
значения функции могут быть больше этого максимума. Поэтому такой максимум назы-вается локальным (местным). Аналогично определяется локальный минимум. Точки локального максимума и минимума называются точками локального экстремума, а значе-ния функции в них – локальными экстремумами функции.
Если функция 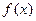 определена на отрезке
определена на отрезке 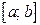 и имеет локальный экстремум на каком-то из концов этого отрезка, то такой экстремум будем называть локальным односторонним или краевым экстремумом. В этом случае соответствующая окрестность является правой для a и левой для b полуокрестностью.
и имеет локальный экстремум на каком-то из концов этого отрезка, то такой экстремум будем называть локальным односторонним или краевым экстремумом. В этом случае соответствующая окрестность является правой для a и левой для b полуокрестностью.

Рассмотрим условия существования экстремума функции. Необходимое условие экстремума примем без доказательства.
Теорема 16.13. (необходимое условие экстремума) Если дифференцируемая функция  имеет экстремум в точке
имеет экстремум в точке  , то ее производная в этой точке равна нулю:
, то ее производная в этой точке равна нулю:  .
.

Отметим, что обратная теорема неверна, т.е. если  , то это не значит, что
, то это не значит, что  – точка экстремума.
– точка экстремума.
Точки, в которых производная равна нулю, называются стационарными (крити-ческими или «подозрительными» на экстремум). Точки, в которых функция непре-рывна, но производная не существует или бесконечна, также являются критическими, так как это тоже точки, где может быть экстремум.
Например, для функции  ее производная
ее производная  равна нулю при
равна нулю при  , но
, но  не является точкой экстремума. Непрерывная функция
не является точкой экстремума. Непрерывная функция  в точке
в точке  производной не имеет, но точка
производной не имеет, но точка  – точка минимума.
– точка минимума.
Теорема 16.14. (первое достаточное условие экстремума) Пусть точка  – критическая, т.е.
– критическая, т.е.  или
или  не существует. Предположим, что в некоторой окрестности
не существует. Предположим, что в некоторой окрестности  для
для  существует конечная производная
существует конечная производная  и она сохраняет свой знак слева и справа от
и она сохраняет свой знак слева и справа от  . Тогда:
. Тогда:
1) если  при
при  и
и  при
при  , т.е. при переходе через
, т.е. при переходе через  производная изменяет знак с «+» на «-», то в точке
производная изменяет знак с «+» на «-», то в точке  функция
функция 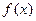 имеет максимум;
имеет максимум;
2) если  при
при  и
и  при
при  , т.е. при переходе через
, т.е. при переходе через  производная изменяет знак с «-» на «+», то в точке
производная изменяет знак с «-» на «+», то в точке  функция имеет минимум;
функция имеет минимум;
3) если при переходе через  знак производной
знак производной  не изменяется, то экстре-мума в точке
не изменяется, то экстре-мума в точке  нет.
нет.
Доказательство. Действительно, в первом случае на 
 возрастает, а на
возрастает, а на  убывает, т.е. в точке
убывает, т.е. в точке  функция имеет максимум.,
функция имеет максимум.,
Теорема 16.15. (второе достаточное условие экстремума) Если  – крити-ческая точка, т.е.
– крити-ческая точка, т.е.  , и функция
, и функция  в точке
в точке  имеет вторую производную
имеет вторую производную  , то в случае
, то в случае 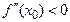 функция имеет в точке
функция имеет в точке  максимум, а при
максимум, а при  – минимум.
– минимум.
Доказательство. Если  существует, то
существует, то  существует в точке
существует в точке  и в некоторой ее окрестности
и в некоторой ее окрестности  . Тогда
. Тогда
 .
.
Если  , то
, то  и при
и при  получаем
получаем  , т.е.
, т.е. 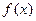 возрастает, а при
возрастает, а при 
 , т.е.
, т.е. 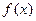 убывает.
убывает.
Таким образом, при переходе через  производная
производная  изменяет знак с отрицательного на положительный и в точке
изменяет знак с отрицательного на положительный и в точке  функция
функция 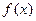 имеет минимум.
имеет минимум.
Пусть 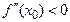 , тогда
, тогда  . При
. При 
 , а при
, а при 
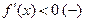 следовательно, имеем максимум.,
следовательно, имеем максимум.,
Надо отметить, что т. 16.15. не применима, если 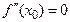 или
или  не существует.
не существует.
Пример 16.21. Найти точки экстремума и промежутки возрастания и убывания для функции:
 .
.
Решение. Функция определена и дифференцируема на 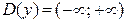 . Ее производная равна
. Ее производная равна 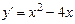 . Необходимое условие экстремума:
. Необходимое условие экстремума:  . Имеем
. Имеем  . Получили две критические точки, которые разбивают всю область определения на три интервала
. Получили две критические точки, которые разбивают всю область определения на три интервала  . Применим первое достаточное условие экстремума, т.е. на рисунке отметим знаки первой производной и стрелками поведение функции на каждом интервале
. Применим первое достаточное условие экстремума, т.е. на рисунке отметим знаки первой производной и стрелками поведение функции на каждом интервале

Точка  – точка максимума.
– точка максимума.  .
.
Точка  – точка минимума.
– точка минимума.  .
.
На интервалах  и
и 
 , следовательно, функция возрастает, на интервале
, следовательно, функция возрастает, на интервале  – функция убывает.
– функция убывает.
II способ.
Вместо исследования перемены знака первой производной можно найти значения второй производной в критических точках:  .
.  , т.е. в точке
, т.е. в точке  вторая производная отрицательна, то в этой точке функция имеет максимум, а если в точке
вторая производная отрицательна, то в этой точке функция имеет максимум, а если в точке  вторая производная положительна, то в этой точке функция имеет минимум.,
вторая производная положительна, то в этой точке функция имеет минимум.,




