Средней величиной в статистике называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности.
Средняя - это сводная характеристика закономерностей процесса в тех условиях, в которых он протекает. Однако для того, чтобы средний показатель был действительно типизирующим, он должен определяться не для любых совокупностей, а только для совокупностей, состоящих из качественно однородных единиц. Это является основным условием научно обоснованного использования средних.
Выбор вида средней определяется экономическим содержанием определенного показателя и исходных данных. В каждом конкретном случае применяется одна из средних величин: арифметическая, гармоническая, геометрическая, квадратическая, кубическая и т.д.
Перечисленные средние относятся к классу степенных средних объединяются общей формулой* (при различных значениях т);
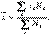
где х — среднее значение исследуемого явления;
т — показатель степени средней;
х - текущее значение (вариант) осредняемого признака;
п — число признаков.
В зависимости от значения показателя степени т различают следующие виды степенных средних:
при т = -1 — средняя гармоническая;
при т = 0 — средняя геометрическая;
при от = 1 — средняя арифметическая;
при т = 2 — средняя квадратическая;
при т = 3 — средняя кубическая.
Помимо степенных средних в статистической практике используются средние структурные, в качестве которых рассматриваются мода и медиана.
Остановимся подробнее на степенных средних.
Средняя арифметическая
Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц.
Чтобы исчислить среднюю арифметическую, нужно сумму всех значений признаков разделить на их число.
Средняя арифметическая применяется в форме простой средней и взвешенной средней. Исходной, определяющей формой, служит простая средняя.
Средняя арифметическая простая равна простой сумме отдельных значений осредняемого признака, деленной на общее число этих значений (она применяется в тех случаях, когда имеются несгруппированные индивидуальные значения признака).
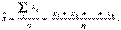
Средняя из вариантов, которые повторяются различное число раз, или, как говорят, имеют различный вес, называется взвешенной. В качестве весов выступают численности единиц в разных группах совокупности (в группу объединяют одинаковые варианты). Средняя арифметическая взвешенная — средняя сгруппированных величин — вычисляется по формуле:
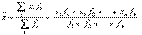
Вычисление средней арифметической часто сопряжено с большими затратами времени и труда. Однако в ряде случаев процедуру расчета средней можно упростить и облегчить, если воспользоваться ее свойствами.
Средняя гармоническая.
Когда статистическая информация не содержит частот f по отдельным вариантам х совокупности, а представлена как их произведение хf, применяется формула средней гармонической взвешенной. Чтобы исчислить среднюю, обозначим хf = w, откуда f = w/x. Используем введенные обозначения и получим формулу средней гармонической взвешенной:
В тех случаях, когда вес каждого варианта равен единице (индивидуальные значения обратного признака встречаются по одному разу), применяется средняя гармоническая простая, исчисляемая по формуле:
Средняя геометрическая
Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т.е. характеризует средний коэффициент роста.
Средняя геометрическая исчисляется извлечением корня степени из произведений отдельных значений — вариантов признака х:
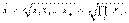
Наиболее широкое применение средняя геометрическая получила для определения средних темпов изменения в рядах динамики, а также в рядах распределения.
Средняя квадратическая и средняя кубическая
В ряде случаев в экономической практике возникает потребность расчета среднего размера признака, выраженного в квадратных или кубических единицах измерения. Тогда применяется средняя квадратическая (например, для вычисления средней величины стороны п квадратных участков, средних диаметров труб, стволов и т.п.) и средняя кубическая (например, при определении средней длины стороны п кубов). Формулы для расчета средней квадратической:
Средняя квадратическая простая является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:
;средняя квадратическая взвешенная 
Формулы для расчета средней кубической аналогичны:
средняя кубическая простая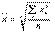 
;средняя кубическая взвешенная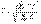 
Средние квадратическая и кубическая имеют ограниченное применение в практике статистики. Широко пользуется статистика средней квадратической, но не из самих вариантов х, и из их отклонений от средней при расчете показателей вариации.
(ПРО МОДУ И МЕДИАНУ В БИЛЕТЕ №16)
