Федеральное агентство по образованию
Новосибирский государственный университет экономики и управления (НИНХ)
Кафедра финансов
Г.М. Кошкина Л.В. Коява
Справочник формул по учебной дисциплине
Финансовый менеджмент
Учебное пособие
Новосибирск 2007
В справочнике представлены основные формулы, используемые в финансовых расчётах при принятии стратегических и тактических управленческих решений руководителями коммерческих организаций. Рассмотрены основы управления временной стоимостью денег, инвестициями, капиталом, риском, доходностью, задолженностью, слиянием и поглощением организации.
Материал пособия основан на специальной учебной литературе, богатом практическом опыте, изложен в соответствии с государственным стандартом подготовки специалистов финансового менеджмента.
Справочник позволит разобраться в конкретных финансовых ситуациях, овладеть навыками расчётов по движению финансовых средств. Рекомендуется для студентов, аспирантов, слушателей факультативов повышения квалификации и практиков, специализирующихся в области управления корпоративными финансами.
Учебное издание
Кошкина Галина Михайловна
Коява Людмила Валерьевна
Введение в финансовый менеджмент
Финансовый менеджмент представляет в первую очередь совокупность научных теорий, правил и методов управления денежными потоками, подготовки и принятия финансовых управленческих решений для достижения целей деятельности организации. Он базируется на ряде взаимосвязанных концепций, разработанных в рамках теории финансов. Это концепции денежного потока, временной ценности денежных ресурсов, компромисса между риском и доходностью, цены капитала, стоимости бизнеса, асимметричности информации, дивидендной политики, агентских отношений.
Во-вторых, финансовый менеджмент – это система рационального управления процессами финансирования деятельности организации, которая включает движение финансовых ресурсов, формирования и рационального использования капитала, управления доходностью и рисками.
Конечной целью такого управления является максимизация стоимости организации (корпорации) путём получения прибыли и её реинвестирования в бизнес при допустимом уровне риска. Финансовый менеджмент включает стратегию и тактику управления. Основные функции финансового менеджмента с точки зрения объектов управления состоят из:
־ Управления денежными потоками и временной стоимостью денег;
־ Управления активами, оптимизации их состава;
־ Управления капиталом (собственным и заёмным), оптимизация его структуры;
־ Управления инвестициями (реальными и финансовыми);
־ Управления финансовыми рисками и предотвращением банкротства.
Все перечисленные функции тесно связаны, хотя иногда носят разнонаправленный характер. Их выполнение возможно в результате финансовых расчётов, анализе финансового состояния и финансовых результатов деятельности организации, анализе альтернативных вариантов решения поставленных целей. Достигнуть это можно путём познания методов расчёта финансовых показателей, оценки факторов, влияющих на эти показатели.
Поэтому к функциям финансового менеджмента с точки зрения субъектов управления относятся:
־ Прогнозирование, планирование финансовых показателей, организация деятельности, учёт, контроль, анализ и принятие управленческих решений.
Инструментом выполнения этих функций являются способы и методы расчёта финансовых показателей. Составители данного пособия обобщили основные формулы финансового менеджмента по главным разделам управления корпоративными финансами.
Раздел 1. Сущность, содержание, цели и задачи финансового менеджмента
Финансовые расчеты по оценке стоимости денег с учетом их использования и фактора времени
1.1.1. Нахождение будущей стоимости (наращение) однократного вложения денежных средств – (Future Value)
1. Наращение по простым ставкам ссудного процента
(1.1)
где FV – будущая стоимость (сумма)
РV – первоначальная стоимость (сумма);
r – ставка годовая процентная;
n – количество лет.
Начисление процентов (по ставке r) происходит на одну и ту же первоначальную стоимость (PV) каждый период времени. То есть суммы процентов по периодам равны между собой. Считается, что инвестиция сделана на условиях простого процента, если инвестированный капитал каждый период времени (ежегодно) увеличивается на сумму PV*r. Коэффициент r можно использовать как дорму дисконта или норму прибыли.
2. Наращение по сложным ставкам ссудного процента
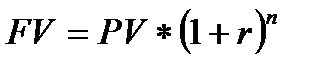(1.2)
Инвестиция, сделана на условиях сложного процента, если очередной годовой доход исчисляется не с исходной величины инвестированного капитала, а с общей суммы, включающей также и ранее начисленные и невостребованные инвестором проценты. В этом случае происходит капитализация процентов по мере их начисления, т.е. база, с которой начисляются проценты, всё время возрастает.
Значение показателя (1+r)n представляет собой коэффициент наращения, который показывает стоимость одной денежной единицы, которая имеется в настоящий момент времени, в будущем. Когда n имеет большое значение, проведение расчетов усложняется. Для этого используются специальные (финансовые) калькуляторы для финансовых расчетов, либо специальные таблицы. Для расчета коэффициента наращения можно воспользоваться таблицей, приведенной в Приложении 1.
3. Наращение, когда проценты начисляются несколько раз в год
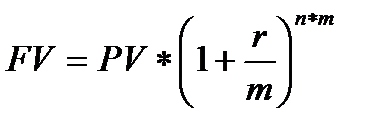(1.3)
где m – количество периодов начисления внутри года.
Существует множество финансовых инструментов, по которым платежи (доходы или расходы) осуществляются чаще одного раза в год, например, по полугодиям, ежеквартально, ежемесячно. Тогда, в расчете будущей стоимости используется количество начислении в год – m. При этом ставка r/m будет соответствовать начислению за один интервал (полугодие, квартал, месяц и т.д.), произведение покажет общее количество начислений за период n. Для расчета будущей стоимости также можно воспользоваться таблицей в Приложении 1.
Кнаращ = 
(1.4)
r = 
(1.5)
Для исчисления показателя роста (Кнаращ.) сравнивается наращенная сумма с первоначальной суммой, относительный показатель прироста характеризует процентную ставку начисления.
4. Наращение при начислении процентов за дробное число лет.
Некоторые финансовые контракты заключаются на период, отличающийся от целого числа лет. В этом случае проценты могут начисляться одним из двух методов:
־ по формуле сложных процентов
FV = PV*(1+r)w + f (1.6)
־ по смешанной схеме (используется схема сложных процентов для целого числа лет и схема простых процентов – для дробной части)
FV = PV*(1+r)w *(1+f*r) (1.7)
где w – целое число лет;
f – дробная часть года.
5. Начисление по внутригодовым подпериодам, когда продолжительность периода не равна целому числу подпериодов.
Этими формулами можно воспользоваться, когда начисление процентов осуществляется за внутригодовой подпериод, а продолжительность общего периода действия контракта не равна целому числу подпериодов. Например, m=2; w=4; f=0,5; r=0,16
־ по схеме сложных процентов
FV = PV* (1+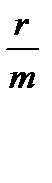 
)w+f (1.8)
־ по смешанной схеме
FV = PV *(1+ 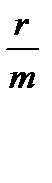)w *(1+f 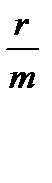) (1.9)
Процентные и учетные ставки решают одни и те же задачи: определяют степень доходности при операциях наращения или размеры дисконтированных сумм при учетных операциях. В связи с этим существует выбор таких процентных и учетных ставок, при использовании которых финансовые последствия окажутся равноценными (эквивалентными).
6. Эквивалентность процентной и учетной ставок при наращении по простым процентам задается равенством эффективных ставок
(1.10)
где re – эффективная процентная ставка;
de – эффективная учетная ставка;
t – период начисления.
7. Эквивалентность процентных и учетных ставок при наращении по сложным процентам выводится из формулы:
(1.11)
Ставки re и de в этом случае являются эквивалентными или релятивными (относительными), они приносят одинаковый доход при начислении процентными и в одинаковом промежутке времени.
Если процентная или учетная ставка изменяются во времени, тогда эквивалентная ставка простых процентов находится по средней арифметической
r = 
(1.12) d = 
(1.13)
где ti – продолжительность периода начисления (временной интервал)
Очевидно, что для эквивалентной ставки выполняется неравенство d<r. Поэтому для сопоставления доходностей различных вариантов сделок, при изменении условий расчетов, исчисляют эквивалентные ставки. При расчете эквивалентных ставок следует иметь ввиду, что для каждого периода начисления необходимо рассчитывать свою эквивалентную ставку.
