Выражение 
(1)
где (uk)kÎN — заданная числовая последовательность, называется числовым рядом. Конечные суммы S1 = u1, S2 = u1 + u2,.... Sn = u1 + u2 +...+ un, называются частичными суммами ряда (1).
Если существует конечный предел последовательности частичных сумм (2)
то ряд (1) называется сходящимся, а число S—суммой ряда (1)
Необходимое условие сходимости. Если ряд (1) сходится, то 
Доказательство.
Пусть ряд u1+u2+…+un… сходится, то есть существует конечный предел 
=S. Тогда имеет место также равенство 
=S, так как при n 
и (n-1) . Вычитая почленно из первого равенства второе, получаем 
- = 
= 
un=0, что и требовалось доказать.
Критерий Коши. Для того чтобы числовой ряд (1) был сходящимся, необходимо и достаточно, чтобы для любого ε > 0 существовало N = N(ε) такое, что для всех n > N и р = 1, 2, … выполнялось неравенство
|
Доказательство:
Вопрос 26 Ряды с неотрицательными членами. Необходимое и достаточное условие сходимости. Признак сравнения.
Положительный ряд сходится тогда и только тогда, когда последовательность его частичных сумм ограничена сверху.
Необходимое условие
Так как ряд сходится, то последовательность частичных сумм имеет предел. Следовательно она ограничена. А значит она ограничена и снизу и сверху. Доказано
Достаточное условие
Дан положительный ряд и последовательность частичных сумм ограничена сверху. Покажем, что наша последовательность(из членов ряда) неубывающая: S(n + 1) − S(n) = a(n + 1) Теперь используем свойство из теоремы о монотонной последовательности и получим, что последовательность частичных сумм ограничена сверху.
Признак сравнения. Пусть даны два ряда с положительными членами
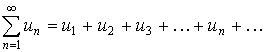(17)
и
(18)
и каждый член ряда (17) не превосходит соответствующего члена ряда (18), т.е. выполняется 
(n = 1, 2, 3, …). Тогда, если сходится ряд (18), то сходится и ряд (17). Если ряд (17) расходится, то ряд (18) также расходится. Этот признак остается в силе, если условие выполняется не для всех n, а лишь начиная с некоторого номера n = N.
Вопрос 27 Признаки Даламбера и Коши сходимости рядов с неотрицательными членами.
Признак Даламбера
Пусть дан знакоположительный числовой ряд
(7)
и пусть существует предел 
При p<1 ряд (7) сходится, при p>1 ряд (7) расходится.
Доказательство. По условию существует предел 
. Это означает, что для любого положительного числа Е существует такой номер N, что для всех номеров n³N выполняется условие 
или
p-E< 
(10)
Пусть сначала p<1. Выберем Е так, что p+E=q<1. Для всех n³N имеем 
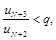… или
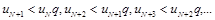
или
(11)
Рассмотрим ряды
(12)
. (13)
Ряд (13) сходится, так как он является бесконечно убывающей геометрической прогрессией. Тогда ряд (12) сходится, учитывая (11), по признаку сравнения. Ряд (7) сходится по теореме 1.
Пусть теперь p>1. Выберем Е так, что p-E>1. Тогда из левой части неравенства (10) следует, что при n³N выполняется 
или un+1>un, то есть члены ряда возрастают с возрастанием номера n. Поэтому un¹0, следовательно, ряд расходится по следствию из необходимого признака сходимости. Теорема доказана.
Замечания.
1. Если расходимость ряда установлена с помощью признака Даламбера, то un¹0.
2. При р=1 признак Даламбера не даёт ответа о сходимости ряда. В этом случае нужно применять другие признаки сходимости.
3. Признак Даламбера рекомендуется применять при наличии в выражении общего члена ряда показательной функции или факториала.
Признак Коши
Пусть дан знакоположительный числовой ряд u1+u2+…+un… (7)
и пусть существует предел 
При p<1 ряд (7) сходится, при p>1 ряд (7) расходится.
Доказательство. По условию существует Это означает, что для любого положительного числа Е существует такой номер N, что для всех n³N выполняется условие | 
| <E или
p-E< 
<p+E. (14)
Пусть p<1. Выберем Е таким, чтобы выполнялось p+E=q<1. Тогда из (14) получаем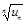 
<q или un<qn для всех n³N. Рассмотрим ряды
(15)
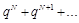(16)
Ряд (16) сходится, так как он является бесконечно убывающей геометрической прогрессией. Ряд (15) сходится, учитывая, что un<qn для всех n³N, по признаку сравнения, следовательно, по теореме 1 сходится ряд (7).
Пусть теперь p>1. Выберем Е так, чтобы выполнялось условие
p-E >1. Тогда из (14) получаем 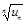>1 или un>1, следовательно, un¹0 и ряд (7) расходится по следствию из необходимого признака сходимости. Теорема доказана.
| Вопрос 28 Знакопеременные ряды. Абсолютная сходимость. Знакочередующиеся ряды. Признак сходимости Лейбница. |
Числовые ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными рядами.
Числовой ряд вида u1-u2+u3-u4+…+ +(-1)n-1.un+…, где un – модуль члена ряда, называется знакочередующимсячисловым рядом.
Если сходится и сам знакопеременный ряд и ряд, составленный из абсолютных величин его членов, то говорят, что знакопеременный ряд сходится абсолютно.
Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин членов этого ряда, расходится, то говорят, что знакопеременный ряд сходитсяусловно.
Признак Лейбница
Если для знакочередующегося числового ряда
 (19)
Выполняются два условия:
Члены ряда убывают по модулю u1>u2>…>un>…,
то ряд (19) сходится, причём его сумма положительна и не превосходит первого члена ряда.
Доказательство. Рассмотрим частичную сумму чётного числа членов ряда S2n=(u1-u2)+(u3-u4)+…+(u2n-1-u2n).
По условию u1>u2>…>u2n-1>u2n, то есть все разности в скобках положительны, следовательно, S2n возрастает с возрастанием n и S2n>0 при любом n.
С другой стороны S2n=u1-[(u2-u3)+(u4-u5)+…+(u2n-2-u2n-1)+u2n]. Выражение в квадратных скобках положительно и S2n>0, поэтому S2n<u1 для любого n. Таким образом, последовательность частичных сумм S2n возрастает и ограничена, следовательно, существует конечный S2n=S. При этом 0<S≤u1.
Рассмотрим теперь частичную сумму нечётного числа членов ряда S2n+1=S2n+u2n+1. Перейдём в последнем равенстве к пределу при n→∞: S2n+1= S2n+ u2n+1=S+0=S. Таким образом, частичные суммы как чётного, так и нечётного числа членов ряда имеют один и тот же предел S, поэтому Sn=S, то есть данный ряд сходится. Теорема доказана.
Замечания.
1. Теорема Лейбница справедлива и если условие un>un+1 выполняется, начиная с некоторого номера N.
2. Условие un>un+1 не является необходимым. Ряд может сходиться, если оно не выполняется.
|
