Свойства определителей.
Транспонирование не меняет определителя. (Транспонирование – взаимная замена строк и столбцов.)
 =
= 
Возьмём любой член определителя (-1)ti+tjai1j1*ai2j2*ai3j3*…*ainjn.
Из вида любого члена определителя видно, что при транспонировании они не меняются.
det AT = det A
1) Если в определителе поменять местами 2 строки, то знак определителя поменяется на противоположный.
Доказательство: Берём произвольный член определителя. Взаимное расположение -> поменялись первые 2 индекса -> чётность изменилась -> изменился знак.
2) Если в определителе 2 строки (столбца) одинаковы, то det = 0.
Если 2 одинаковые строки поменять местами, то ничего не меняется, но по св-ву 2 знак меняется. Это происходит, если △=0. (△=-△, 2△=0, △=0)
3) Если в определителе есть 2 пропорциональные строки, то он тоже = 0.
det  = k det
= k det 
после того, как k вынесен, 2 строки равны. По св-ву 3 △ =0.
4) Если в некоторой строке определителя все элементы в виде 1 и той же комбинации чисел, а именно k-я строка (αck1 + βdk1 + αck2+ βdk2) = α|ck1+ck2…+ckn|+β|dk1+dk2…+dkn|.
5) Если в любой строке определителя прибавить любую другую строку с противоположным коэффициентом, то определитель не изменится.
6) Если строка в определителе состоит из нулей, то определитель = 0.
7) Если какая-либо строка определителя есть линейная комбинация других строк, то определитель = 0.
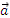 1 = (a11,a1n)
1 = (a11,a1n)
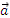 2 = (a21,a2n)
2 = (a21,a2n)
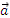 n = (an1,ann)
n = (an1,ann)
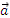 1 1
| |
| Det A= | 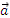 2 2
|
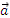 n n
|
Пусть 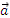 k есть линейная комбинация остальных
k есть линейная комбинация остальных
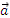 k = α1
k = α1 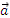 1 + α2
1 + α2 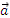 2 +…+ αk-1
2 +…+ αk-1 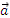 k-1 + αk+1
k-1 + αk+1 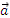 k+1 +…+ αn
k+1 +…+ αn 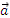 n
n
В соответствии со свойством 7 определитель равен сумме этих определителей, равных нулю. Количество определителей = (n-1)и в каждой из которых имеются одинаковые строки.
Разложение определителя по элементам строки или столбца.
Минором элемента определителя aik называется определитель n-1 порядка, получающийся вычёркиванием строки и столбца, на пересечении которых стоит элемент aik.
Алгебраическим дополнением Аik элемента определителя aik называется Aik = (-1)i+kMik.
Теорема. Определитель равен сумме произведений элементов какой-либо строки на их алгебраические дополнения.
det A = ak1Ak1+ak2Ak2+…+aknAkn = 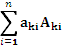
1) Доказательство: Пусть определитель имеет вид:
 =
= 
a11 
Определитель 1 порядка, полученный вычёркиванием 1 строки и 1 столбца.
Тем самым, для 1 случая теорема доказана.
2) Пусть определитель имеет вид:
 = (-1)j
= (-1)j
an1 an2 an3 an4 … anm
Передвинем последовательными шагами столбец этого элемента akj (столбец с номером j) влево до занятия им места 1 столбца. При этом определитель при каждом шаге меняет знак и итоге приобретает множитель (-1)j и приобретает вид:

anj an1 an2 an3 … anm
Далее перемещаем строку с номером k вверх последовательно, пока она не займёт место 1ой строки, т.е. определитель будет иметь вид:

anj an1 an2 an3 … anm
При этом определитель приобретает ещё один множитель (-1)k. В итоге

anj an1 an2 an3 … anm
Мы пришли к 1 случаю, для которого справедливость была доказана.
det A = (-1)j+kakjMkj+0*Ak1+…+0*Ak2 *…*0*Akn
3) Общий случай.
| a11 | a12 | … | a1m |
| … | … | … | … |
| ak1 | ak2 | … | akm |
| … | … | … | … |
| an1 | an2 | … | anm |
=(-1)k+1ak1Mk1+(-1)k+2ak2Mk2+…+(-1)k+naknMkn
Это правило вычисления определителя называется разложением по I строке (столбцу).
2. Равенство нулю суммы произведений элементов строки (столбца, алгебраическое дополнение другой строки (столбца)).
Сумма произведений элементов какой-либо строки на алгебраическое дополнение другой строки равна нулю, т.е.:
(*) аk1Аj1+ аk2Аj2+…+ аknАjn=0
Доказательство:
Рассмотрим определитель:
| … | … | … | … | ||
| j-я строка | aj1 | aj2 | ajn | = аj1Аj1+ аj2Аj2+…+ аjnАjn (**) | |
| k-я строка | ak1 | ak2 | akn |
В выражении (*) коэффициент Аjm получились вычёркиванием j-ой строки -> аjmА не зависят от тех чисел, которые могут стоять в j-ой строке.
В определителе (**) на место j-ой строки поставим k-ую строчку. Тогда этот определитель равен det А = аk1Аj1+ аk2Аj2+…+ аknАjn
Но это равенство равно нулю, так как определитель имеет две одинаковые строки. Ч.т.д.
3. Ранг матрицы. Вычисление ранга методом окаймляющих миноров.
Пусть имеется прямоугольная матрица nхm.
Минором K-ого порядка матрицы А (k<m,k<n) называется определитель, получающийся из элементов, стоящих на пересечении каких-либо строк и каких-либо столбцов.
Рангом матрицы называется целое, положительное число r=Rang А, такое, что в данной матрице присутствует хотя бы один минор порядка r≠0, а все миноры следующего порядка (r+1 и далее) =0.
Метод окаймления миноров.
Если в матрице найден отличный от нуля минор k-ого порядка, то все миноры k+1 порядка считать не обязательно, так как имеет место теорема:
Если все окаймляющие данный минор k-ого порядка миноры k+1 порядка равны нулю, то и все вообще миноры k+1 –ого порядка = 0.
Найдём окаймляющие миноры 3-его порядка для M2: (положим, М2≠0)
| а11 | а12 | а13 | а14 |
| а21 | а22 | а23 | а24 |
| а31 | а32 | а33 | а34 |
| а41 | а42 | а43 | а44 |
| а11 | а12 | а13 | |
| M3(1)= | а21 | а22 | а23 |
| а31 | а32 | а33 |
| а11 | а13 | а14 | |
| M3(2)= | а21 | а23 | а24 |
| а31 | а33 | а34 |
| а11 | а12 | а13 | |
| M3(3)= | а21 | а22 | а23 |
| а41 | а42 | а43 |
| а11 | а13 | а14 | |
| M3(4)= | а21 | а23 | а24 |
| а41 | а43 | а44 |
4. Теорема о базисном миноре. Понятие линейно независимых строк (столбцов) определителя. Необходимое и достаточное условие равенства 0 определителя.
При нахождении ранга матрицы минор порядка r (ранг матрицы) называется базисным.
Все строки матрицы являются линейными комбинациями строк базисного минора. (к столбцам относится то же самое).
Доказательство:
| a11 | a12 | … | a1r | a1j | a1r+1 | … | a1n |
| a21 | a22 | … | a2r | a2j | a2r+1 | … | a2n |
| a31 | a32 | … | a3r | a3j | a3r+1 | … | a3n |
| … | … | … | … | … | … | … | … |
| ar1 | ar2 | … | arr | arj | arr+1 | … | arn |
| ak1 | ak2 | … | akr | akj | akr+1 | … | akn |
| am1 | am2 | … | amr | аmj | amr+1 | … | amn |
Берём любую строку с номером произвольным k. Ставим её под базисный минор. Вправо от минора ставим произвольный столбец с номером j. Рассмотрим минор Mr+1, окаймляющий базисный снизу. K-ой строкой, справа k-ым столбцом.
Разложим его:
Mr+1=0=c1a1j+ c2a2j+ crarj+ Arakj |:Ar (Ar≠0)
Akj=-c1*a1j/Ar- c2*a2j/Ar+…- cr*arj/Ar
Так как akj – координаты вектора строки с номером k, это вернодля любого столбца (коэффициенты ci/Ar одинаковы для любого j) -> сам вектор
строка ak=-c1a1/Ar- c2a1/Ar -crar/Ar
Следствие из теоремы о базисном миноре:
Определитель матрицы равен нулю тогда и только тогда, когда ранг матрицы <n (порядок квадратной матрицы)
Доказательство:
| а11 | а12 | … | а1n |
| а21 | а22 | … | а2n |
| аm1 | аm2 | … | аmn |
det A = 0
Rang A < n
1) Необходимость: дано: det A = 0, доказать: Rang A<n
Так как det A = 0, то по карйней мере одна из строк есть линейная комбинация строк. Это значит, что число линейно независимых строк < n. Число линейно независимых строк и есть Rang A -> r<n
2) Достаточность: дано: Rang A<n, доказать: det A = 0
Так как Rang A<n, а ранг – число линейно независимых строк, то в А число линейно независимых строк <n. Значит, по крайней мере одна из строк есть линейная комбинация остальных, а это значит, что det A = 0 (по св-вам определителя).
Ранг матрицы равен числу линейно независимых строк (столбцов), так как если методом Гаусса с помощью элементарных преобразований привести матрицу к виду трапеции, то оставшиеся строки являются линейно независимыми.
| а11 | а12 | … | а1n |
| а21 | а22 | … | а2n |
| аm1 | аm2 | … | аmn |
Рассмотрим строки как векторы (координаты aij (j=1,2,3…n))
1=(а11, а12, а13,…,а1n);
 2=(а21, а22, а23,…,а2n);
2=(а21, а22, а23,…,а2n);
 m=(аm1, аm2, аm3,…,аmn);
m=(аm1, аm2, аm3,…,аmn);
Строки называются линейно независимыми, если они линейно независимы в смысле векторов, т.е. единственная линейная комбинация векторов, равная 0, это та, все коэффициенты нули.
Линейная комбинация – с1  1 + с2
1 + с2  2 + … + сm
2 + … + сm  m равна нулю тогда и только тогда, когда все числовые коэффициенты с1 = с2 = сn = 0. Тогда векторы линейно независимы.
m равна нулю тогда и только тогда, когда все числовые коэффициенты с1 = с2 = сn = 0. Тогда векторы линейно независимы.
Если вектор – линейная комбинация остальных, то система линейно зависима: ak= с1  1 + с2
1 + с2  2 + … + сk-1
2 + … + сk-1  k-1 + сk+1
k-1 + сk+1  k+1 + сn
k+1 + сn  n
n
5. Системы линейных алгебраических уравнений. Правило Крамера.
х1, х2, …, хn – неизвестные
aik – постоянные коэффициенты
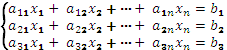
Матрица системы:
| а11 | а12 | … | а1n |
| а21 | а22 | … | а2n |
| аm1 | аm2 | … | аmn |
1) Кмножаем каждую строку системы на алгебраическое дополнение 1-ого элемента строки.
2) Сложим уравнения.
 *x1 +
*x1 +  *x2 + … +
*x2 + … +  *xn =
*xn = 
3) Поступим так же со вторым столбцом. (каждый элемент строки умножаем на А второго элемента строки). Слева получим △х2, справа - △2
Если определитель системы △≠0, то система имеет, и притом единственное, решение, даваемое формулами крамера:

△ – определитель системы, составленный из коэффициентов при неизвестных.
△i – определитель, получаемый из определителя системы △ заменой столбца коэффициентов при неизвестном определяемом столбце свободных членов.
Если определитель системы △ = 0:
Если хотя бы один △i ≠ 0, то система несовместна (ᴓ) (решений нет)
Если все △i = 0, то решение существует и их бесконечно много. Система несовместна и называется неопределённой.
В случае неопределённой системы не все числа х1, х2, …, хn можно брать произвольными, так как даже если одно уравнение осталось в системе, а все остальные – следствие из него, то это уравнение связывает между собой переменные, а это и значит, что все их брать произвольными нельзя.
6. Необходимое и достаточное условие совместимости системы. Теорема Кронекера – Капелле.
Система совместна тогда и только тогда, когда Rang А, составленный из коэффициентов при неизвестных, равен Rang Yрасширенной матрицы, т.е. матрицы, которая получена из матрицы A присоединением к ней столбца свободных членов.
| а11 | а12 | … | а1n | b1 |
| а21 | а22 | … | а2n | b2 |
| аm1 | аm2 | … | аmn | b3 |
Rang A = Rang 
Вектор столбец
(*) a1x1 + a2x2 +…+ anxn =b
1) Необходимость: Дано: совместная система, доказать: Rang A = Rang 
Доказательство: Так как система совместна, то есть, имеет решение, то существует такой набор чисел x1=c1, x2=c2, xn=cn, при подставлении которых в систему (*) получится верное равенство. Следовательно, b есть линейная комбинация остальных столбцов.
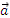 1x1 +
1x1 + 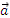 2x2 +…+
2x2 +…+ 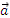 nxn =
nxn = 
->  линейная комбинация столбцов
линейная комбинация столбцов 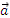 . Если в матрице
. Если в матрице  один столбец является линейной комбинацией остальных, то при добавлении к матрице А этого столбца, её Rang не меняется, т.е. Rang A = Rang
один столбец является линейной комбинацией остальных, то при добавлении к матрице А этого столбца, её Rang не меняется, т.е. Rang A = Rang 
2) Достаточность:
Дано: Rang A = Rang 
Доказать: система (*) совместна.
Доказательство: Матрицы A и  отличаются только
отличаются только  и т.к. их ранги равны, то дабавление к А
и т.к. их ранги равны, то дабавление к А  не меняет её ранга. Значит, этот столбец – линейная комбинация остальных столбцов. Т.е. существует такие числа c1, c2, c3,…,cn, что
не меняет её ранга. Значит, этот столбец – линейная комбинация остальных столбцов. Т.е. существует такие числа c1, c2, c3,…,cn, что 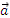 1c1+
1c1+ 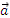 2c2+…+
2c2+…+ 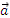 ncn=
ncn=  . Но это и есть система (*)
. Но это и есть система (*)
-> (*) удовлетворилась при x1=c1, x2=c2, xn=cn ч.т.д.
Т.е. с1,с2,сn – решения системы.
Метод Гаусса решения систем линейных алгебраических систем уравнений.
Метод Гаусса. Пусть дана система  линейных уравнений с
линейных уравнений с  неизвестными
неизвестными  . Выпишем расширенную матрицу системы/
. Выпишем расширенную матрицу системы/  Цель алгоритма -- с помощью применения последовательности элементарных операций к матрице
Цель алгоритма -- с помощью применения последовательности элементарных операций к матрице  добиться, чтобы каждая строка, кроме, быть может, первой, начиналась с нулей, и число нулей до первого ненулевого элемента в каждой следующей строке было больше, чем в предыдущей. Находим первый ненулевой столбец в матрице
добиться, чтобы каждая строка, кроме, быть может, первой, начиналась с нулей, и число нулей до первого ненулевого элемента в каждой следующей строке было больше, чем в предыдущей. Находим первый ненулевой столбец в матрице  . Пусть это будет столбец с номером
. Пусть это будет столбец с номером  . Находим в нем ненулевой элемент и строку с этим элементом меняем местами с первой строкой. Чтобы не нагромождать дополнительных обозначений, будем считать, что такая смена строк в матрице
. Находим в нем ненулевой элемент и строку с этим элементом меняем местами с первой строкой. Чтобы не нагромождать дополнительных обозначений, будем считать, что такая смена строк в матрице  уже произведена, то есть
уже произведена, то есть  . Тогда ко второй строке прибавим первую, умноженную на число
. Тогда ко второй строке прибавим первую, умноженную на число  , к третьей строке прибавим первую, умноженную на число
, к третьей строке прибавим первую, умноженную на число  , и т.д. В результате получим матрицу
, и т.д. В результате получим матрицу
 Если в матрице
Если в матрице  встретилась строка с номером
встретилась строка с номером  , в которой все элементы
, в которой все элементы  равны нулю, а
равны нулю, а  , то выполнение алгоритма останавливаем и делаем вывод, что система несовместна. Действительно, восстанавливая систему уравнений по расширенной матрице, получим, что
, то выполнение алгоритма останавливаем и делаем вывод, что система несовместна. Действительно, восстанавливая систему уравнений по расширенной матрице, получим, что  -ое уравнение будет иметь вид
-ое уравнение будет иметь вид

Этому уравнению не удовлетворяет ни один набор чисел  Матрицу
Матрицу  можно записать в виде
можно записать в виде
 где
где 
По отношению к матрице  выполняем описанный шаг алгоритма. Получаем матрицу
выполняем описанный шаг алгоритма. Получаем матрицу
 где
где  ,
,  . Эту матрицу снова можно записать в виде
. Эту матрицу снова можно записать в виде
 и к матрице
и к матрице 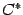 снова применим описанный выше шаг алгоритма.
снова применим описанный выше шаг алгоритма.
Процесс останавливается, если после выполнения очередного шага новая уменьшенная матрица состоит из одних нулей или если исчерпаны все строки. Заметим, что заключение о несовместности системы могло остановить процесс и ранее. Если бы мы не уменьшали матрицу, то в итоге пришли бы к матрице вида

Далее выполняется так называемый обратный ход метода Гаусса. По матрице  составляем систему уравнений. В левой части оставляем неизвестные с номерами, соответствующими первым ненулевым элементам в каждой строке, то есть
составляем систему уравнений. В левой части оставляем неизвестные с номерами, соответствующими первым ненулевым элементам в каждой строке, то есть  . Заметим, что
. Заметим, что  . Остальные неизвестные переносим в правую часть. Считая неизвестные в правой части некоторыми фиксированными величинами, несложно выразить через них неизвестные левой части. Теперь, придавая неизвестным в правой части произвольные значения и вычисляя значения переменных левой части, мы будем находить различные решения исходной системы
. Остальные неизвестные переносим в правую часть. Считая неизвестные в правой части некоторыми фиксированными величинами, несложно выразить через них неизвестные левой части. Теперь, придавая неизвестным в правой части произвольные значения и вычисляя значения переменных левой части, мы будем находить различные решения исходной системы  . Чтобы записать общее решение, нужно неизвестные в правой части обозначить в каком-либо порядке буквами
. Чтобы записать общее решение, нужно неизвестные в правой части обозначить в каком-либо порядке буквами  , включая и те неизвестные, которые явно не выписаны в правой части из-за нулевых коэффициентов, и тогда столбец неизвестных можно записать в виде столбца, где каждый элемент будет линейной комбинацией произвольных величин
, включая и те неизвестные, которые явно не выписаны в правой части из-за нулевых коэффициентов, и тогда столбец неизвестных можно записать в виде столбца, где каждый элемент будет линейной комбинацией произвольных величин  (в частности, просто произвольной величиной
(в частности, просто произвольной величиной  ). Эта запись и будет общим решением системы. Если система была однородной, то получим общее решение однородной системы. Коэффициенты при
). Эта запись и будет общим решением системы. Если система была однородной, то получим общее решение однородной системы. Коэффициенты при  , взятые в каждом элементе столбца общего решения, составят первое решение из фундаментальной системы решений, коэффициенты при
, взятые в каждом элементе столбца общего решения, составят первое решение из фундаментальной системы решений, коэффициенты при 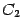 -- второе решение и т.д. Фундаментальную систему решений однородной системы можно получить и другим способом. Для этого одному переменному, перенесенному в правую часть, нужно присвоить значение 1, а остальным -- нули. Вычислив значения переменных в левой части, получим одно решение из фундаментальной системы. Присвоив другому переменному в правой части значение 1, а остальным -- нули, получим второе решение из фундаментальной системы и т.д. Замечание 15.4 У читателя может возникнуть вопрос: "Зачем рассматривать случай, когда некоторые столбцы матрицы
-- второе решение и т.д. Фундаментальную систему решений однородной системы можно получить и другим способом. Для этого одному переменному, перенесенному в правую часть, нужно присвоить значение 1, а остальным -- нули. Вычислив значения переменных в левой части, получим одно решение из фундаментальной системы. Присвоив другому переменному в правой части значение 1, а остальным -- нули, получим второе решение из фундаментальной системы и т.д. Замечание 15.4 У читателя может возникнуть вопрос: "Зачем рассматривать случай, когда некоторые столбцы матрицы  нулевые? Ведь в этом случае соответствующие им переменные в системе уравнений в явном виде отсутствуют." Но дело том, что в некоторых задачах, например, при нахождении собственных чисел матрицы, такие системы возникают, и игнорировать отсутствующие переменные нельзя, так как при этом происходит потеря важных для задачи.
нулевые? Ведь в этом случае соответствующие им переменные в системе уравнений в явном виде отсутствуют." Но дело том, что в некоторых задачах, например, при нахождении собственных чисел матрицы, такие системы возникают, и игнорировать отсутствующие переменные нельзя, так как при этом происходит потеря важных для задачи.












 .
.






