
Рекомендации по решению задачи:
1. Решить задачу, используя ППП Eureka.
2. Исходя из полученного решения, выбрать границы существования корня.
3. Составить блок – схему решения и программу на QBasic.
Контрольные вопросы
«Уточнение корня уравнения»
1. В чем заключается геометрический смысл метода половинного деления?
2. Какой оператор цикла используется в процедуре дихотомии?
3. Какими свойствами должна обладать функция F(x), чтобы методом половинного деления можно было гарантировать решение уравнения F(x)?
4. Что необходимо для нахождения хотя ы одного действительного корня уравнения F(x) методом половинного деления?
5. Какие процедуры функции используются в программе?
6. Какой функцией заменяется левая часть уравнения F(x)=0 в методе итерации?
7. Что называется сходимостью метода итерации?
8. Каково условие сходимости метода итерации и как это условие проверяется в программе?
9. В чем заключается геометрическая интерпретация метода Ньютона?
10. Исходя из чего выбирается в методе Ньютона первое приближение Х0
11. Для чего в программе предусмотрена процедура-функции для второй производной от исходной функции?
Варианты заданий для самостоятельного решения
Задание.
1. Уточнить корень уравнения, используя следующие методы:
- метод половинного деления;
- метод простой итерации;
- метод касательных (Ньютона).
2. Для вариантов заданий, представленных в таблице 4, выбрать точность вычисления.
3. Для вариантов заданий, представленных в таблице 6, вычислить корень с заданной точностью.
4. Для вариантов заданий, представленных в таблице 7,8,9, установить границы существования корня, точность вычисления, установить границы существования корня.
Таблица заданий № 4.
| П\П | Вид уравнения | Начальное приближение корня |
| 1. | x – sin 2x – 1 = 0 | |
| 2. | 2x ^ 3 + 4x – 1 = 0 | 0.1 |
| 3. | x ^ 3 + 12x – 2 = 0 | 0.95 |
| 4. | 5 – x – 8lnx = 8 | 4.32 |
| 5. | x ^ 3 + x = 1000 | 9.42 |
| 6. | x – sin x = 0.25 | 1.17 |
| 7. | x ^ 3 – 6x ^ 2 + 20 = 0 | 2.25 |
| 8. | 5x ^ 3 + 10x ^ 2 + 5x – 1 = 0 | 0.6 |
| 9. | 3sin  +0.34x-3.8 =0 +0.34x-3.8 =0
| |
| 10. | x – 3 + sin (3.6x) = 0 | |
| 11. | arcos(x)- 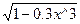 = 0 = 0
| |
| 12. | √1- 0.4x ^ 2 – arcsin x = 0 | |
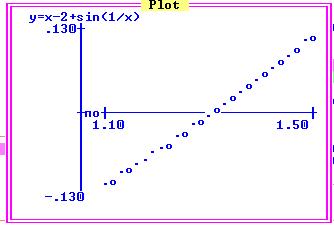
| 13. | x – 2 + sin x = 0 | 1.2 |
| 14. | 1 – x + sin x – ln (1 + x) = 0 | |
| 15. | x ^ 2 – ln (1 + x) – 3 = 0 | |
| 16. | x ^ 3 + x ^ 2 – 3 = 0 | 0.6 |
| 17. | x ^ 3 – x – 0.2 = 0 | 0.9 |
| 18. | 5x ^ 3 – x – 1 = 0 | 0.6 |
| 19. | x ^ 3 – 2x – 5 = 0 | 1.9 |
| 20. | x ^ 3 + x = 1000 | 9.1 |
| 21. | x ^ 4 + 2x ^ 3 – x – 1 = 0 | |
| 22. | x ^ 3 – x – 2 = 0 | 0.9 |
| 23. | x – sin x/2 – 1 = 0 | |
| 24. | 2 ^ 3 + 4x – 1 = 0 | 0.1 |
| 25. | x ^ 3 + 12x – 2 = 0 | 0.95 |
Таблица заданий № 5
| П\П | Вид уравнения | Отрезок |
| 1. | 0.25x ^ 3 + x – 1.2502 = 0 | 0, 2 |
| 2. | 0.1x ^ 2 – xlnx = 0 | 1, 2 |
| 3. | 3x – 4lnx – 5 = 0 | 2, 4 |
| 4. | e ^ x – e ^ -x – 2 = 0 | 0, 1 |
| 5. | e ^ x + lnx – 10x = 0 | 3, 4 |
| 6. | 3x – 14 + e ^ x – e ^ -x = 0 | 1, 3 |
| 7. | 3ln ^ 2x + 6lnx– 5 = 0 | 1, 3 |
| 8. | 2xsinx – cosx = 0 | 0.4, 1 |
| 9. | xtgx – 1\3 = 0 | 0.2, 1 |
| 10. | √ 1 – x - cos√ 1 – x = 0 | 0, 1 |
Таблица заданий № 6
| № вар. | Уравнение | Интервал | Точность |
| 1. | x – 1\ (2 + sin2x) = 0 | [0; 1] | 10 ־³ |
| 2. | arcsin(x\3) - √ 1 – (x\3) ^ 2 = 0 | [ 1,5; 3] | 10 ־³ |
| 3. | x - √ 9 –x+ x ^ 2 = 0 | [1; 2] | 10 ־³ |
| 4. | √1 – x ^ 2 - arcsin x = 0 | [0; 1] | 10 ־³ |
| 5. | tgx – (1/3)(tgx)^3 + (1/5)(tg x) ^ 5 – 1/3 = 0 | [0; 0,8] | 10 ־³ |
| 6. | e ^ x – e (- x) – 2 = 0 | [0; 1] | 10 ־³ |
| 7. | cosx – e(-(x ^ 2) / 2) + x – 1 = 0 | [0; 2] | 10 ־³ |
| 8. | sin(x ^ 2) + cos(x ^ 2) – 10x = 0 | [0; 1] | 10 ־³ |
| 9. | 3sin√x + 0,35x – 3,8 = 0 | [2; 3] | 10 ־³ |
| 10. | √1 – 0,04 (x ^ 2) – x = 0 | [0; 1] | 10 ־³ |
| 11. | 1/4(x ^ 3) + x – 1,25 = 0 | [0; 1] | 10 -5 |
| 12. | x – sin(x + 2) = 0 | [0; 1] | 10 -5 |
| 13. | √1 – x - cos√1 – x = 0 | [0; 1] | 10 ־³ |
| 14. | 0,1(x ^ 2) – x lnx = 0 | [1; 2] | 10 ־³ |
| 15. | 3x – 4 lnx – 5 = 0 | [1;4] | 10 ־³ |
| 16. | e ^ x + lnx – 10 x = 0 | [1; 4] | 10 ־³ |
| 17. | x tgx – 1/3 = 0 | [0; 1] | 10 ־³ |
| 18. | 0,25(x ^ 3) + x – 1,25 = 0 | [0; 2] | 10 ־³ |
| 19. | 3x – 14 + e ^ x + e (-x) = 0 | [1; 3] | 10 ־³ |
| 20. | 2x sinx – cosx = 0 | [0,4; 1] | 10 ־³ |
| 21. | 1/(1 + x ^ 2) – x = 0 | [1; 2] | 10 ־³ |
| 22. | .(tg x) ^ 2 – x = 0 | [1; 2] | 10 ־³ |
| 23. | x + ln(х + 0.5) - 0.5 = 0 | [0;2] | 10 ־³ |
| 24. | x ^3 – х - 0.2 = 0 | [1;1,1] | 10 ־³ |
| 25. | x^ 4 + 2х^ 3 – х – 1 = 0 | [0; 1] | 10 ־³ |
| 26. | x ^ 3 – 0.2х^ 2 - 0.2х - 1.2 = 0 | [1;1,5] | 10 ־³ |
| 27. | 2sin^2х/3 – Зсоs^2х/4 = 0 | [0;П/2] | 10־³ |
| 28. | x ^ 4 + 0.8х ^ 3 - 0.4х ^ 2 - 1.4х - 1.2 = 0 | [-1,2;-0,5] | 10־³ |
| 29. | x ^ 4 - 4.1х ^ 3 + х^ 2 - 5.1х + 4.1 = 0 | [3,7;5] | 10־³ |
| 30. | х2 ^ х – 1 = 0 | [0;1] | 10־³ |
Таблица заданий № 7
| № вар | Уравнение | № вар | Уравнение |
| 1. | x – sinx = 0,25 16. | 16. | tg(0,3x + 0,4) = x ^ 2 |
| 2. | tg(0,58x + 0,1) = x ^ 217. | 17. | x ^ 2 – 20sinx = 0 |
| 3. | √x – cos(0,387x) = 018. | 18. | ctgx – x/4 = 0 |
| 4. | tg(0,4x + 0,4) = x ^ 2 19. | 19. | tg(0,47x + 0,20 = 0 |
| 5. | lgx – 7/(2x + 6) = 020. | 20. | x ^ 2 + 4sinx = 0 |
| 6. | tg(0,5x + 0,2) = x ^ 2 21. | 21. | ctgx – x/2 = 0 |
| 7. | 3x – cosx – 1 = 022. | 22. | 2x – lgx – 7 = 0 |
| 8. | x + lgx = 0,523. | 23. | tg(0,44x + 0,30 = 0 |
| 9. | tg(0,5x + 0,1) = x ^ 2 24. | 24. | 3x – cosx – 1 = 0 |
| 10. | x ^ 2 + 4sinx = 025. | 25. | ctgx – x/10 = 0 |
| 11. | ctg1,05x – x ^ 2 = 026. | 26. | x ^ 2 + 4sinx = 0 |
| 12. | tg(0,4x + 0,3) = x ^ 2 27. | 27. | tg(0,36x + 0,4) = 0 |
| 13. | xlgx – 1,2 = 028. | 28. | x + lgx = 0,5 |
| 14. | 1,8x ^ 2 – sin10x = 0 29. | 29. | ctgx – x/5 = 0 |
| 15. | ctgx – x/4 = 030. | 30. | 2lgx – x/2 + 1 = 0 |
Таблица заданий № 8
| № вар | Уравнение | № вар | Уравнение |
| 1. | x ^ 3 – 3x ^ 2 + 9x – 8 = 0. | x ^ 3 + 4x – 6 = 0 | |
| 2. | x ^ 3 – 6x – 8 = 0 | x ^ 3 + 0,2x ^ 2 + 0,5x + 0,8 = 0 | |
| 3. | x ^ 3 – 3x ^ 2 + 6x + 3 = 0 | x ^ 3 – 3x 62 + 12x – 12 = 0 | |
| 4. | x ^3 – 0,1x ^ 2 + 0,4x –1,5 = 0 | x ^3 -0,2 x^2 + 0,3x + 1,2 = 0 | |
| 5. | x ^ 3 – 3x ^ 2 + 9x + 2= 0 | x ^ 3 – 2x + 4 = 0 | |
| 6. | x ^ 2 + x – 5 = 0 | x ^ 3 – 0,2x ^ 2 + 0,5x – 1,4 = 0 | |
| 7. | x ^ 3+ 0,2 x ^2 +0,5x –1,2 = 0 | x ^ 3 – 3x ^ 2 + 6x – 5 = 0 | |
| 8. | x ^ 3 + 3x + 1 = 0 | x ^ 3 – 0,1x ^ 2 + 0,4x + 1,2 = 0 | |
| 9. | x ^ 3 + 0,2x ^ 2 + 0,5x – 2 = 0 | x ^ 3 – 0,2x ^ 2 + 0,5x – 1 = 0 | |
| 10. | x ^ 3 – 3x ^ 2 + 12x – 9 = 0 | x ^ 3 + 3x ^ 2 + 12x + 3 = 0 | |
| 11. | x ^3 –0,2x ^ 2 + 0,3x – 1,2 = 0 | x ^ 3 – 0,1x ^ 2 + 0,4x + 2 = 0 | |
| 12. | x ^ 3 – 3x ^ 2 + 6x – 2 = 0 | x ^ 3 – 0,2 x ^ 2 + 0,4x – 1,4 = 0 | |
| 13. | x ^ 3 –0,1x ^ 2 +0,4x –1,5 = 0 | x ^ 3 + 0,4x ^ 2 + 0,6x – 1,6 = 0 | |
| 14. | x ^ 3 + 3x ^ 2 + 6x – 1 = 0 | x ^3 + x – 3 = 0 | |
| 15. | x ^ 3 +0,1x ^ 2+0,4x –1,2 = 0 | x ^ 3 – 0,2x ^ 2 + 0,5x + 1,4 = 0 |
Таблица заданий № 9
| № вар | Уравнение | № вар | Уравнение |
| 1). | 2x ^ 3 – 3x ^ 2 – 12x – 5 = 0 | 2x ^ 3 – 3x ^ 2 – 12x + 1 = 0 | |
| 2). | x ^ 3 – 3x ^ 2 – 24x – 3 = 0 | x ^ 3 – 3x ^ 2 – 24x – 5 = 0 | |
| 3). | x ^ 3 – 3x ^ 2 + 3 = 0 | x ^ 3 – 4x ^ 2 + 2 = 0 | |
| 4). | x ^ 3 – 12x + 6 = 0 | x ^ 3 – 12x – 5 = 0 | |
| 5). | x ^ 3 + 3x ^ 2 – 24x – 10 = 0 | x ^ 3 + 3x ^ 2 – 24x + 1 = 0 | |
| 6). | 2x ^ 3 – 3x ^ 2 – 12x + 10 = 0 | 2x 6 3 – 3x^ 2 – 12x + 12 = 0 | |
| 7). | 2x ^ 3 + 9x ^ 2 – 21 = 0 | 2x ^ 3 + 9x ^ 2 – 6 = 0 | |
| 8). | x ^ 3 – 3x ^ 2 + 2,5 = 0 | x ^ 3 – 3x ^ 2 + 1,5 = 0 | |
| 9). | x ^ 3 + 3x ^ 2 – 2 = 0 | x ^ 3 – 3x ^ 2 – 24x + 10 = 0 | |
| 10). | x ^ 3 + 3x ^ 2 – 3,5 = 0 | x ^ 3 + 3x ^ 2 – 24x – 3 = 0 | |
| 11). | x ^ 3 + 3x ^ 2 – 24x + 10 = 0 | x ^ 3 – 12x – 10 = 0 | |
| 12). | x ^ 3 – 3x ^ 2 – 24x – 8 = 0 | 2x ^ 3 + 9x ^ 2 – 4 = 0 | |
| 13). | 2x ^ 3 + 9x ^ 2 – 10 = 0 | 2x ^ 3 – 3x ^ 2 – 12x + 8 = 0 | |
| 14). | x^ 3 – 12x + 10 = 0 | X ^ 3 + 3x ^ 2 – 1 = 0 | |
| 15). | x ^ 3 +3x ^ 2 – 3 = 0 | x ^ 3 – 3x ^ 2 + 3,5 = 0 |
ЛАБОРАТОРНАЯ РАБОТА № 4
«Методы численного решения дифференциальных уравнений.
Уравнения 1-го порядка»
Цель работы
Ознакомление с принципом модульного программирования на примере задачи решения дифференциальных уравнений и использование оболочки QBasic для построения подпрограмм и головного модуля.
Порядок выполнения работы
1. Получить у преподавателя вариант задания, включающий в себя
· дифференциальное уравнение (F(x))
· интервал (а,b)
· шаг (h)
· краевое значение функции (у 0 )
2. Написать подпрограмму для каждого метода (Эйлера, Эйлера-Коши,
Рунге-Кутта)
3. Написать подпрограмму процедуры-функции
4. Написать головной модуль
5. Отладить программу и получить результаты
6. Построить график решений дифференциального уравнения для всех 3-х методов в Excel.
Содержание отчета
1. Содержательная постановка задачи
2. Исходные данные
3. Краткое описание методов
4. Блок схема подпрограмм и блок схема головного (или управляющего) модуля
5. Листинг подпрограмм и управляющего модуля
6. Распечатка полученных результатов
7. Распечатка результатов в Excel.
Теоретические сведения






