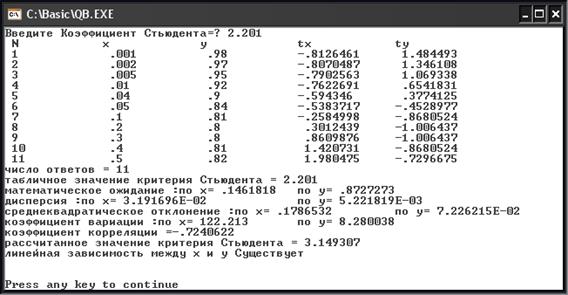
ПРИМЕР РАБОТЫ в EXCEL
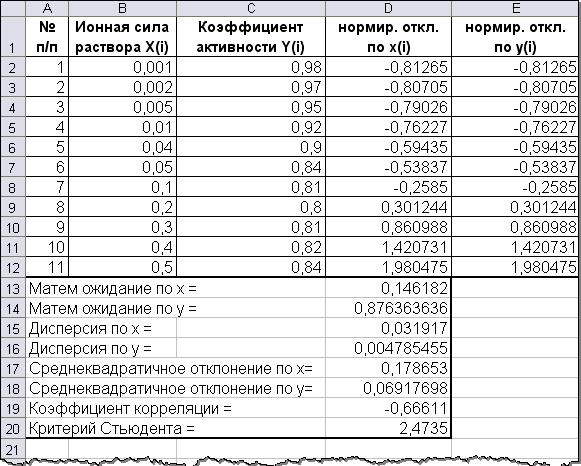
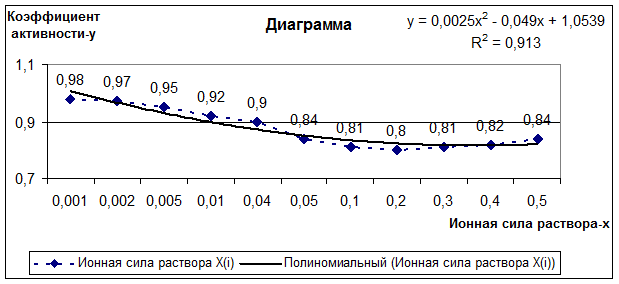
 Результаты эксперимента
Результаты эксперимента
Контрольные вопросы
«Статистическая обработка результатов эксперимента»
1. Что характеризует математическое ожидание?
2. Какие характеристики оценивают разброс случайных величин?
3. Как определяется дисперсия?
4. Для чего необходим коэффициент вариации?
5. Как определить нормированное отклонение?
6. Что характеризует коэффициент корреляции?
7. В каких пределах измеряется коэффициент корреляции?
8. Как определить уровень значимости коэффициента корреляции?
9. Как выбирается Ттабл?
10. Какое соотношение должно быть между Трасч и Ттабл, для утверждения, что линейная зависимость существует?
ЛАБОРАТОРНАЯ РАБОТА № 2
«Численное интегрирование»
Цель работы.
Ознакомится с принципом модульного программирования на примере задачи численного интегрирования. Использование оболочки QBASIC для построения процедур программ.
Основные теоретические сведения.
|
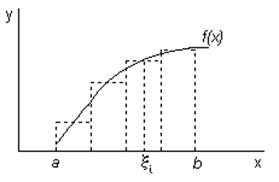
Пусть на отрезке [а,b] задана функция f(x). Определенный интеграл определяется как площадь, ограниченная подынтегральной функцией f(x), осью x и ординатами в точках «a» и «b»
Определенным интегралом от функции f(x) на отрезке [а, b] называется предел интегральной суммы при неограниченном увеличении числа точек разбиения.
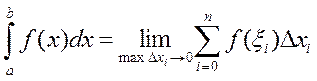
Во многих случаях, когда подынтегральная функция задана в аналитическом виде, определенный интеграл удается вычислить непосредственно по формуле Ньютона-Лейбница. Она состоит в том, что определенный интеграл равен приращению первообразной F(х) на отрезке интегрирования. На практике этой формулой часто нельзя воспользоваться по двум основным причинам:
Вид функции не допускает непосредственного интегрирования, т.е. первообразную нельзя выразить в элементарных функциях
Значения функций f(х) заданы таблично (множество хi конечно)
В этих случаях используются методы численного интегрирования.
Частным случаем в методах численного интегрирования является тот, когда величина элементарного отрезка ∆х,- величина постоянная и может быть вынесена за знак интегральной суммы. Эта величина называется шагом интегрирования и обозначается обычно ∆х.
Рассмотрим методы численного интегрирования.
Метод прямоугольников
В Методе прямоугольников непосредственно используется замена определенного интеграла интегральной суммой. В качестве точек xi; могут выбираться левые (xi-1) или правые ( xi) границы элементарных отрезков. Расчетные формулы можно записать так:
При выборе левых границ (см. рис.1)
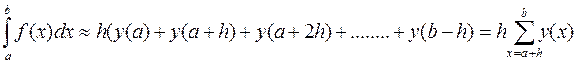
 |
При выборе правых границ (см. рис.2)
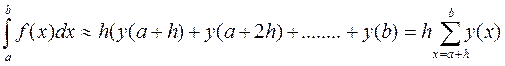
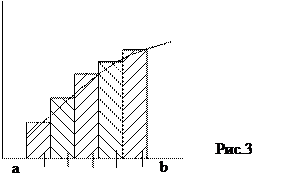 |
При выборе границ от a+ h/2 до b-h/2
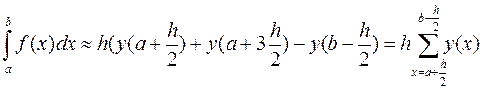
 |
Рис.4
Метод трапеций
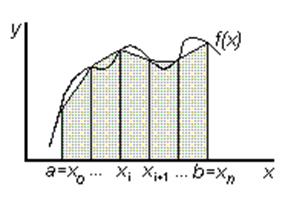
|
В методе трапеций график функции f(х)аппроксимируется ломаной, соединяющей точки с координатами
(xi, у)
Рис.5
Искомое значение определенного интеграла представляется в виде суммы площадей трапеций, построенных на каждом из элементарных отрезков:
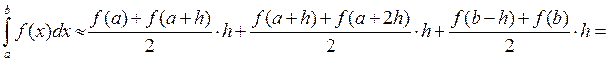
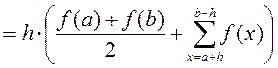
Метод парабол
В методе парабол (формула Симпсона) на каждом из элементарных отрезков по трем известным значениям функции f(Xj) строится парабола, заданная уравнением aх2+bх+с.
Формула для нахождения определенного интеграла может быть выведена из условия равенства значений: уi = aхi2+ bxi +с:
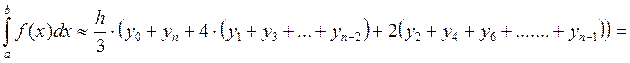
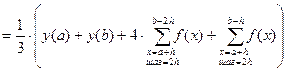
3. Порядок выполнения работы
3.1. Получить у преподавателя вариант задания, включающий в себя подынтегральную функцию (F(Х)), отрезок интегрирования (a,b), точность вычисления значения интеграла (eps).
3.2. Исследовать подынтегральную функцию на непрерывность и существование на заданном отрезке.
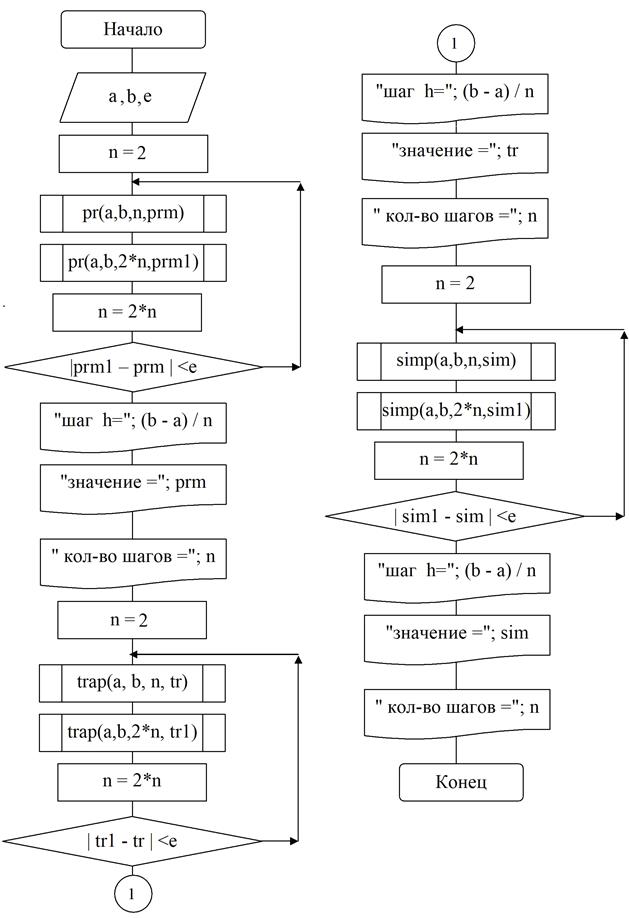
3.3. Составить блок-схему для каждого метода и блок-схему головного модуля.
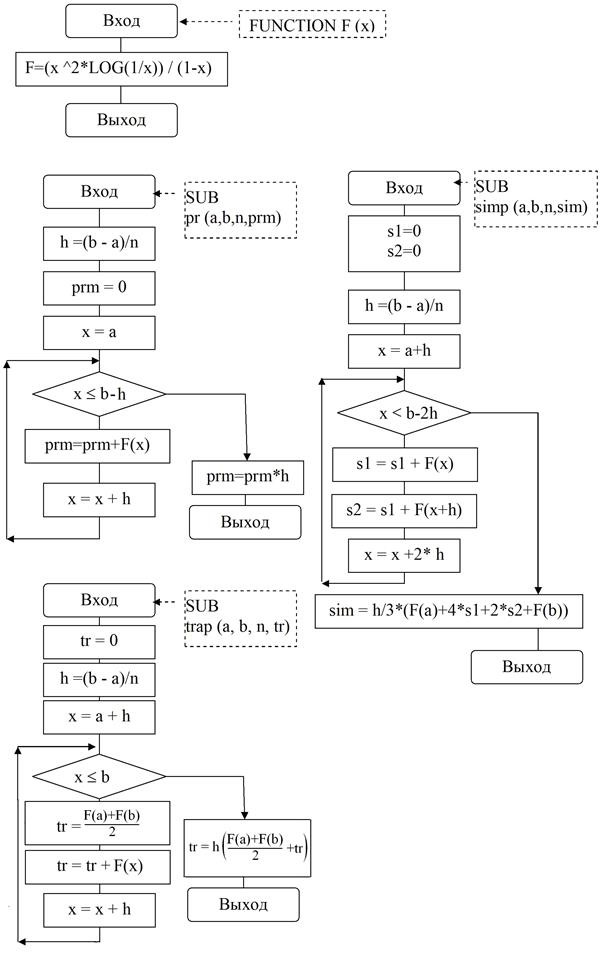
3.4. Написать подпрограмму для каждого метода (прямоугольников, трапеции, парабол).
3.5. Написать головной модуль.
3.6. Отладить программу и получить результаты.
3.7. Проанализировать полученные результаты и сделать выводы.
4. Содержание отчета.
4.1. Математическая постановка задачи.
4.2. Исходные данные.
4.3. Краткое описание методов. Блок-схема для каждого метода. Листинг подпрограмм.
4.4. Блок-схема головного (или управляющего) модуля. Листинг.
4.5. Распечатка полученных результатов.
4.6. Сравнительный анализ полученных результатов разными методами.
Пример выполнения работы
Вычислить интеграл 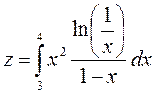
БЛОК-СХЕМА