Постановка задачи.
Дано: Кинематическая схема механизма и его размеры
lAB = 1 м, lBS1 = 2 м, lBD = 0.7м, lAC = 1.45м,
lBS2 = 0.35м, lBS3 = 0.4 м;
массы и моменты инерции звеньев m1 = 1000 кг,
IS1 = 800 кг * м 2, m2 = 50 кг, IS2 = 2 кг * м 2, m3 = 100 кг,
IS3 = 5 кг * м 2; w 1нач = 0, D j 1 = 30°, j 1нач = 0.
____________________________________________
Определить: w 1 = f(j 1), t = f(j 1), w 1 = f(t), e 1 = f(j 1).
1. Выбор динамической модели и определение ее параметров.
|
рис. 7.7
В качестве динамической модели принимаем звено 1, совершающее вращательное движение вокруг точки А с круговой частотой w 1 , положение которого определяется обобщенной координатой j 1 . Параметры динамической модели: суммарный приведенный момент инерции звеньев механизма Iпрå и суммарный приведенный момент, действующих на него внешних сил, Mпрå определяются в следующей последовательности:
1.1. Определение кинематических передаточных функций для звеньев механизма u21 = u31 , центров масс VqS1 , VqS2 и VqS3 и точки приложения движущей силы VqD . Для определения этих функций воспользуемся методом проекций векторного контура механизма.
|
рис. 7.8
Рассмотрим следующие векторные контуры:
l AB = l AC + l CB;
l AD = l AB + l BD;
l AS2 = l AC + l CS2;
l AS3 = l AC + l CS3;
l AS1 = xS1 + yS1.
Для первого векторного контура l AB = l AC + l CB проекции на оси координат
Производные от этих выражений по j 1
позволяют определить первые передаточные функции
Для второго векторного контура l AD = l AB + l BD проекции на оси координат
Производные от этих выражений по j 1
позволяют определить первую передаточную функцию
|
Для третьего векторного контура l AS2 = l AB + l BS2 проекции на оси координат
Производные от этих выражений
позволяют определить первую передаточную функцию
|
Для четвертого векторного контура l AS3 = l AС + l С S3 проекции на оси координат
Производные от этих выражений
позволяют определить первую передаточную функцию
|
Для последнего пятого векторного контура l AS1 = xS1 + yS1 проекции на оси координат
Производные от этих выражений по j 1
позволяют определить первую передаточную функцию
|
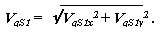
Построим графики передаточных функций и передаточных отношений, которые необходимы для определения параметров динамической модели в нашем примере.
|
рис. 7.9
1.2. Определение движущей силы по условиям в начале и в конце цикла.
Расчет проведем для закона изменения движущей силы, который изображен на рис.7.5. Величина движущей силы в начальном положении механизма рассчитывается по формуле
|
Принимаем k=1.1 и получаем
В конечном положении величина движущей силы рассчитывается по формуле:
|
Значение движущей силы в интервале (b - a)* HD определим по формуле:
F
Примем a = 0.32 и b = 0.65 и рассчитаем перемещения центров масс
подставим полученные значения в формулу и получим
|
|
1.3. Определение приведенного суммарного момента.
|
- 2. определение приведенного суммарного момента сил сопротивления
В нашем примере силами сопротивления являются силы веса звеньев механизма, поэтому расчет суммарного приведенного момента сил сопротивления проводим по формуле
|
- определение приведенного момента движущей силы
В нашем примере только одна движущая сила, создаваемая давлением жидкости в гидроцилиндре. Приведенный момент от этой силы
|
На рис. 7.13 приведены диаграммы приведенных моментов: сопротивления Мпрå с , движущего Мпр Fд i и суммарного Мпрå с = Мпрå + Мпр Fд i .
1.4. Определение суммарного приведенного момента инерции
В рассматриваемом механизме приведенный момент инерции суммируется из масс и моментов инерции звеньев и может быть рассчитан по следующей зависимости
|
|
рис. 7.14
|
рис. 7.15
Графики переменной части суммарного приведенного момента инерции даны на рис. 7.13 и 7.14. Кроме того, имеется и постоянная часть Iпрå c, определяемая массой и моментом инерции звена 1
Суммарный приведенный момент инерции и равен сумме постоянной и переменной частей
2. Определение суммарной работы внешних сил.
Суммарную работу внешних сил получим интегрированием суммарного приведенного момента Мпрå по обобщенной координате dj 1
|
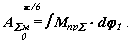
Интегрирование можно проводить различными методами. Воспользуемся методом графического интегрирования. При этом методе участок изменения обобщенной координаты, на котором проводится интегрирование, разбирается на несколько малых частей (в нашем примере 6). В пределах каждого i -го участка кривая Мпрå = f (j 1) заменяется прямой, соответствующей среднеинтегральному значению Мпрå i на этом участке. На продолжении оси абсцисс, влево от начала координат откладываем отрезок интегрирования k1. Ординаты среднеинтегральных значений Мпрå i проецируем на ось ординат. Точки пересечения проецирующих линий с осью ординат соединяем прямыми с концом отрезка интегрирования. На диаграмме работы из начала первого участка (и до его конца) под углом y 1 к оси абсцисс проводим прямую. Для второго участка аналогичная прямая проводится под углом y 2. Ее начало выбирается в точке пересечения предыдущего отрезка прямой с вертикалью проходящей начало второго участка. Проведя построения для всего интервала интегрирования, получим график работы. Масштаб этого графика определим из подобия треугольников
Графики, иллюстрирующие построение диаграммы работы, приведены на рис.7.1 6 и 7.1 7
3. Определение угловой скорости звена приведения
Определение закона движения звена приведения в виде диаграммы изменения угловой скорости в функции обобщенной координаты w 1= f(j 1) проводится по формуле
|
|
|
|
|
рис. 7.18
Диаграмма w 1 = f (j 1) приведена на рис. 7.18.
4. Определение времени цикла.
Время цикла определяется по диаграмме t= f (j 1). Для построения этой диаграммы проведем интегрирование диаграммы угловой скорости
|
Воспользуемся методом графического интегрирования обратной величины. При этом участок изменения обобщенной координаты, на котором проводится интегрирование, разбивается на несколько малых участков. В пределах каждого i -го участка кривая w 1 = f (j 1) заменяется прямой, соответствующей среднеинтегральному значению w 1ср i на этом участке. На оси ординат, откладываем отрезок интегрирования k2 (рис.7.19). Ординаты среднеинтегральных значений w 1ср i проецируем на ось ординат. Точки пересечения проецирующих линий с осью ординат переносим по дугам окружности на продолжение оси абсцисс. Полученные на оси абсцисс точки, соединяем прямыми линиями с концом отрезка интегрирования. Из начала первого участка (на диаграмме времени) и до его конца под углом y 1 к оси абсцисс проводим прямую линию. Для второго участка аналогичная прямая проводится под углом y 2. Ее начало выбирается в точке пересечения предыдущего отрезка прямой с вертикалью проходящей начало второго участка. Проведя построения для всего интервала интегрирования, получим график времени. Масштаб этого графика определим из подобия треугольников
5. Построение диаграммы угловой скорости в функции времени
Диаграмма угловой скорости w 1 = f (t) в функции времени строится по диаграммам w 1 = f (j 1) и t= f (j 1), исключением переменной j 1.
|
|
|
6. Определение углового ускорения звена приведения
Для расчета углового ускорения звена приведения e 1 = f(j 1) можно воспользоваться двумя различными зависимостями:
Применение первой формулы приводит к большим погрешностям, так как она основывается на использовании одной из конечных зависимостей расчета w 1 = f (j 1). Кроме того, в точках с нулевыми значениями w 1 расчет по этой формуле дает неверный результат e 1 = 0. Поэтому проведем расчет зависимости e 1 = f(j 1) по второй формуле. Диаграмма функции e 1 = f(j 1) приведена на рис. 7.22.
|
