Числами
Цель. Научиться вычислять суммы и произведения элементов множеств в цифровом и символьном виде, выполнять операции с комплексными числами.
ХОД РАБОТЫ
1. Для вычисления сумм и произведений воспользуемся панелью Исчислений 
на панели инструментов математика.
Например, вычислим суммы следующих рядов:
;
;
;
.
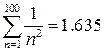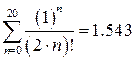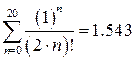Для этого используется значок суммы 
с указанием границ суммирования.
Система, к сожалению, не может считать суммы с бесконечными пределами. В случаях, когда пределы изменения индекса указываются в виде переменной интервального типа (например, для работы с матрицами и функциями, зависящими от индекса) используется знак суммирования только с указанием индекса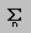 
.
Например, вычислим сумму элементов матрицы:
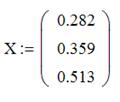
i: = 0..2
.
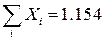2. Вычислить сумму элементов матрицы своего варианта.
3. Аналогично вычисляются произведения.
По определению: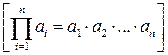 
.
Например, вычислим произведение элементов следующих рядов:
,
,
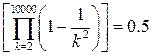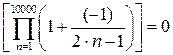х: = 0.5
.
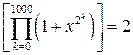4. Вычислим сумму и произведение диагональных элементов для матрицы
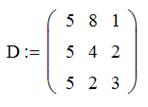
i: = 0..2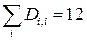 
.
5. MathCADпредусматривает работу с комплексными числами. Комплексные числа вводятся в обычной алгебраической записи, в качестве мнимой единицы используется символ i или j.
Внимание! Для ввода комплексной единицы единице необходимо напечатать «1i» или «1j», или использовать соответствующий знак на панели калькулятора.
Введем два комплексных числа:
a:= 2 + 3i; b:= -1 + 4j
Выполним с ними различные операции.
Сложение:
с:= а + b;
с = 1+7i.
Вычитание:
с:= а – b;
с = 3 – i.
Умножение:
ab = –14 + 5i.
Деление:
.
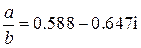Комплексные сопряжения:
;
.
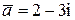Комплексное сопряжение выводится символом двойной кавычки после набора имени переменной (“).
В случае многозначности корней система возвращает корень с наименьшей мнимой частью.
ei = 0.54 + 0.84i,
sin(i) = 1.175i,
cos(i) = 1.543,
,
,
.
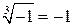Для работы с комплексными числами используются следующие функции:
Re(z) – действительная часть числа;
Im(z) – множественная часть числа;
arg(z) – аргумент (угол в комплексной плоскости между вещественной осью и осью Z);
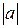– модуль.
В нашем случае:
; 
; 
; 
;
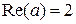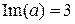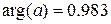R;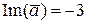 
; 
; 
.
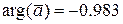6. Выполните индивидуальное задание.
7. Покажите результат преподавателю.
ВАРИАНТЫ ЗАДАНИЙ
Задание для всех вариантов.
1. Вычислить сумму элементов ряда.
2. Вычислить произведение ряда.
3. Вычислить сумму элементов матрицы.
Таблица 2
| № варианта | Ряд
x = 1, 
| Матрица |
| 1. |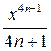 
| 
|
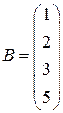
| 2. |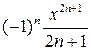 
| 
|
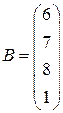
Продолжение табл. 2
| № варианта | Ряд | Матрица |
| 3. |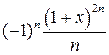 
| 
|
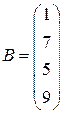
| 4. | 
| 
|
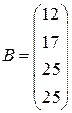
| 5. |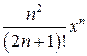 
| 
|
| 6. | 
| 
|
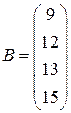
| 7. |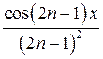 
| 
|
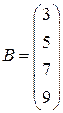
| 8. | 
| 
|
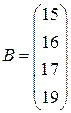
| 9. |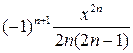 
| 
|
Окончание табл. 2
| № варианта | Ряд | Матрица |
| 10. |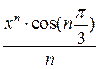 
| 
|
| 11. | 
| 
|
| 12. |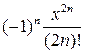 
| 
|
ЛАБОРАТОРНАЯ РАБОТА № 5.
Вычисление пределов, производных, интегралов и логарифмов
Цель. Научиться использовать возможности программы MathCAD для вычисления пределов, производных и интегралов.
ХОД РАБОТЫ
Вычисление пределов, производных, интегралов и логарифмов осуществляется с помощью панели Вычислений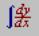 
.
1. Вычисление пределов.
Кнопки 
и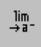 
взять на палитре Вычисления.
Вычислим вначале замечательный предел.
;
;
;
;
.
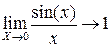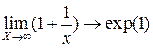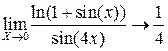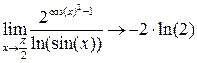Можно также вычислить пределы слева и справа:
– левый предел;
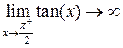– правый предел.
2. Вычисление производной.
Чтобы вычислить производную нужно подставить функцию под знак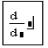 
.
,
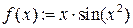– значение первой производной.
- значение производной n -го порядка.
Вычислим производную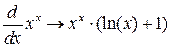 
.
Для вычисления производной функции в точке необходимо определить значение переменной. Зададим:
x:=0.5.
Получаем:
.
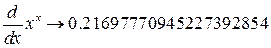(проверим: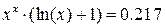 
).
3. Вычисление интегралов.
Вычисление определенных интегралов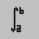 
.
Вычислим интеграл функции:
для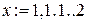 
с точностью 10-8
Точность задается системной переменной TOL, которая может быть определена в меню Математика→Параметры (Math Options).
Установим 10-8.
TOL:=10-8
Определенный интеграл – есть площадь криволинейной трапеции.
.
Вычислим 
интеграл функции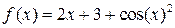 
на отрезке 
.
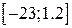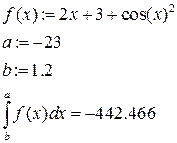
Вычисление неопределенных интегралов 
.
,
.
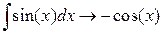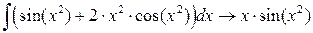Следует иметь в виду, что MathCAD не выводит константу интегрирования.
Вычислим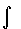 
от более сложной функции:
.
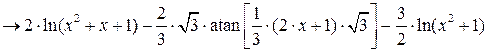4. Вычисление логарифмов.
MathCAD позволяет вычислять логарифмы натуральные, десятичные, и по произвольному основанию от положительных вещественных чисел.
Положительное число: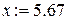 
.
Натуральный логарифм: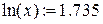 
.
Логарифм по основанию 10: 
.
Логарифм по произвольному основанию:
основание: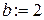 
.
Логарифм по данному основанию: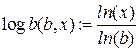 
.
5. Выполните индивидуальное задание. Покажите результат преподавателю.
ВАРИАНТЫ ЗАДАНИЙ
Задание для всех вариантов.
1. Вычислите пределы.
2. Вычислите определенный интеграл.
3. Вычислите неопределенный интеграл.
Таблица 3
| № варианта | Пределы | Интегралы | |
| Определенный a, b, m = 1 | Неопределенный | ||
| 1. |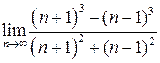 
| 
| 
|
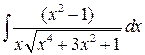
| 2. |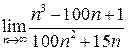 
| 
| 
|
| 3. |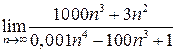 
| 
| 
|
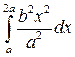
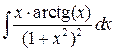
| 4. |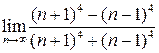 
| 
| 
|
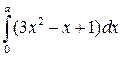
| 5. |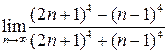 
| 
| 
|
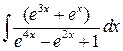
| 6. | 
| 
| 
|
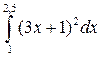
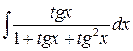
| 7. |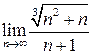 
| 
| 
|
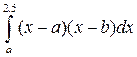
| 8. |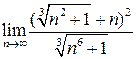 
| 
| 
|
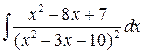
| 9. |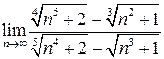 
| 
| 
|
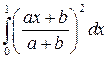
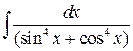
| 10. |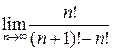 
| 
| 
|
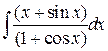
| 11. | 
| 
| 
|
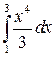
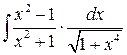
| 12. |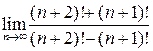 
| 
| 
|
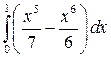
ЛАБОРАТОРНАЯ РАБОТА № 6.
