Цель. Научиться выполнять различные операции с матрицами: вычислять обратную и транспонированную матрицы, производить выборку элементов матрицы, а также решать системы линейных уравнений матричным способом.
ХОД РАБОТЫ
Задание 1. Решить систему линейных уравнений:
1. Запишите ее на рабочем листе MathCAD. Знак равенства здесь вводится при помощи (Ctrl =) или палитры логических операций 
.
2. Составьте матрицу из коэффициентов при неизвестных и присвойте ей значение переменной А. (А – матрица размером 3х3).
.
И матрицу В из коэффициентов свободных членов (В – вектор–столбец размером 3х1).
.
Для ввода используем кнопку «Матрицы» 
. Переход между компонентами матрицы осуществляется с помощью кнопки [TAB].
3. Вычислим обратную матрицу A-1 указав (-1) степень:
4. Решите матричным способом систему линейных уравнений:
X:= A -1∙ B,
где x = (x 1, x 2, x 3) – искомый вектор.
Результат вывести двумя способами:
а) в виде матрицы:
в нашем случае 
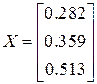
б) в виде отдельных элементов:
в этом случае доступ к элементу матрицы производится по индексу, отсчитывая от 0: X 0 = 0.282, X 1 = 0.359, X 2 = 0.513, где X 0 = x, X 1 = y, X 2 = z.
Задание 2. Выполним операцию транспонирования матрицы A и B выбрав на панели матрицы кнопку 
.
и 
.
Задание 3. Вычислите определитель матрицы с помощью кнопки 
.
Задание 4. Вычислите скалярное и векторное произведение двух векторов a и b:
С помощью кнопки 
и 
:
Скалярное произведение: 
Векторное произведение: 
.
Задание 5. Вычислить сумму элементов вектора В:
.
Задание 6. Произведите выборку различных элементов матрицы:
а) выбор максимального и минимального значения:
max(A)=7; min(A)= –1;
б) извлечение элемента с заданным индексом.
Внимание. По умолчанию столбцы и строки массивов в MathCAD нумеруются, начиная с нуля!
Доступ к элементу матрицы производится по индексам, отсчитываемым от 0; первый из них нумерует строки, второй – столбцы:
Для матрицы А это будет выглядеть так:
A 0,0 = 1, A 0,2 = 0, A 2,2 = 5, A 2,0 = -1.
Индексы разделяются запятыми.
Задание 7. Выполните индивидуальное задание.
ВАРИАНТЫ ЗАДАНИЙ
Вариант 1
Вычислить определитель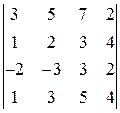 
.
Вариант 2
Найти y из системы уравнений, представив ее в виде матричного уравнения 
Вариант 3
Найти сумму матриц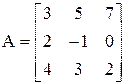 
и 
.
Вариант 4
Найти матрицу 2А+5В, если 
и 
.
Вариант 5
Найти произведения матриц А∙В и В∙А, если 
и 
.
Вариант 6
Найти значение матричного многочлена 
, если 
, а Е – единичная матрица третьего порядка.
Вариант 7
Дана матрица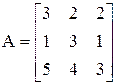 
. Найти обратную матрицу.
Вариант 8
Решить систему уравнений, представив ее в виде матричного уравнения:
Вариант 9
Дана матрица 
. Найти обратную матрицу.
Вариант 10
Найти матрицу А∙В – 2В∙А, если 
и .
Вариант 11
Решить систему уравнений матричным методом:
Вариант 12
Найти матрицу 
, если 
и 
.
ЛАБОРАТОРНАЯ РАБОТА № 3.
