Цель. Научиться решать квадратные уравнения, уравнения с одной производной, а также системы нелинейных уравнений, используя возможности программы MathCAD.
ХОД РАБОТЫ
1. Решение квадратного уравнения.
Программа MathCAD позволяет находить корни многочлена второй степени 
.
Введем коэффициенты а: = 1, b:= –2, с:= –8.
И определим функцию
Переменной 
присваиваем значение
– транспонированная матрица.
Переменной 
присвоим значение функции 
.
Получаем корни: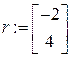 
.
2. Решение уравнения с одной неизвестной.
Рассмотрим одно алгебраическое уравнение с одним неизвестным х.
f (x) = 0, например, sin(x) = 0.
Для решения таких уравнений MathCAD имеет встроенную функцию root, которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента и, соответственно, работает несколько по-разному.
- root (f (х), х);
- root (f (х), х, а, b);
где f (х) – скалярная функция, определяющая уравнение;
х – скалярная переменная, относительно которой решается уравнение;
а, b – границы интервала, внутри которого происходит поиск корня.
Первый тип функции root требует дополнительного задания начального значения (guess value) переменной х. Для этого нужно просто предварительно присвоить х некоторое число. Поиск корня будет производиться вблизи этого числа. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня.
Рис. 2. Решение уравнения
с одной неизвестной в среде MathCAD
Обратите внимание, что хотя уравнение имеет бесконечное количество корней, MathCAD находит (с заданной точностью) только один из них, х 0, лежащий наиболее близко к х = 0,5. Если задать другое начальное значение, то решением будет другой корень уравнения. Таким образом, для поиска корня средствами MathCAD требуется его предварительная локализация. Это связано с особенностями выбранного численного метода, который называется методом секущих.
Иногда удобнее задавать не начальное приближение к корню, а интервал [ а, b ], внутри которого корень заведомо находится. В этом случае следует использовать функцию root с четырьмя аргументами, а присваивать начальное значение х не нужно. Поиск корня будет осуществлен в промежутке между а и b альтернативным численным методом (Риддера или Брента):
.
Когда root имеет четыре аргумента, следует помнить о двух ее особенностях:
- внутри интервала [ а, b ] не должно находиться более одного корня, иначе будет найден один из них, заранее неизвестно какой именно;
- значения f (а) и f (b) должны иметь разный знак, иначе будет выдано сообщение об ошибке.
Иногда алгоритм поиска корня натыкается на локальный минимум функции, при этом появляется сообщение «отсутствие сходимости», в таком случае следует попробовать другое начальное решение.
Для поиска комплексных корней следует задавать комплексное начальное приближение: x: = 1i или 1j.
3. Решение систем линейного уравнения.
Системы линейных уравнений решаются матричным способом (см. лабораторную работу № 2).
Решите следующую систему:
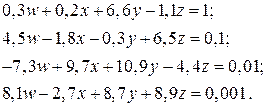
Вектор искомых решений:
.
4. Решение систем нелинейных уравнений.
Используя блок решения уравнений, MathCAD находит решение системы n нелинейных уравнений с n неизвестными.
Зададим начальные приближения для всех неизвестных:
х: = 1 у: = 1 z: = 0.
Вводим уравнения в блок решения уравнений:
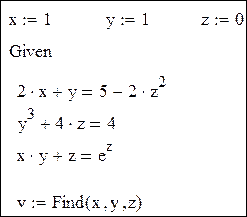
Рис. 3. Фрагмент решения в MathCAD
Найденное решение:
.
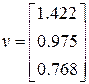5. Выполните индивидуальное задание.
6. Показать результат преподавателю.
ВАРИАНТЫ ЗАДАНИЙ
Задание для всех вариантов.
1. Решить систему линейных уравнений матричным способом.
x 1 + 5 x 2 + x 3 = V + 12
3 x 1 – x 2 + x 3= V – 1
Vx 1 + 3 x 2 + (V +4) x 3 = V (V +2) – 6
Здесь V – номер компьютера.
2. Решить уравнение с одной неизвестной.
Таблица 1
| 1. | 
| Начальное приближение 0 |
| 2. | 
| Начальное приближение 1 |
| 3. |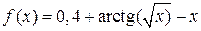 
| Начальное приближение 0 |
| 4. | 
| Начальное приближение 0 |
| 5. | 
| Начальное приближение 0 |
| 6. | 
| Начальное приближение 1 |
| 7. | 
| Начальное приближение 1 |
| 8. | 
| Начальное приближение 0 |
| 9. | 
| Начальное приближение 0 |
| 10. | 
| Начальное приближение 1 |
| 11. | 
| Начальное приближение 0 |
| 12. | 
| Начальное приближение 0 |
ЛАБОРАТОРНАЯ РАБОТА № 4.
