Организация устройств управления с жесткой и гибкой логикой.

Управляющие автоматы со «схемной» логикой

Термин “автомат” используют двояко. В технике с понятием “автомат” связыва­ют некоторое устройство, способное выполнять определенные функции без вмеша­тельства человека или с его ограниченным участием. В другом, широком аспекте, автомат – это математическая модель, отображающая физические или абстрактные явления самой разнообразной природы (вычислительные машины, системы управления и связи, лингвистика и др.). Универсальность теории автоматов позволяет рассматривать с единой точки зрения различные объекты, устанавливать связи и аналогии между ними, переносить результаты исследований из одной области в другую. Обобщенным примером цифрового автомата является компьютер, выполняющий прием, хранение и преобразование дискретной информации по заданным алгоритмам.

Общая теория автоматов подразделяется на абстрактную и структурную. Абстрактная теория изучает поведение автомата относительно внешней среды и не рассматривает способы его построения. Структурная теория автоматов изучает способы построения логических схем автоматов на основе алгоритма, заданного на абстрактном уровне.

Абстрактный автомат как систему задают упорядоченной совокупностью шести объектов {X, Y, Z, ), где:

Х= {x₁, x_2, x_3…. x_m} – множество входных сигналов;

Y= {y₁, y₂, y₃,. y_n} – множество выходных сигналов;

Z = {z₁, z₂, z₃,. z_r} – множество внутренних состояний, определяемых памятью автомата;

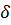— функция переходов, задающая отображение множеств X*Z Z;

— функция выходов, задающая отображение множеств или Z Y;

— начальное состояние автомата.

Множества X, Y, Z называются алфавитами, а их элементы – буквами. Последовательности входных и выходных букв образуют соответственно входные и выходные слова.

Понятие “память” (внутренние устойчивые состояния) автомата введено для описания систем, сигналы на выходах которых зависят как от входных сигналов в данный момент времени, так и от предыдущей истории развития процесса. В общем множество устойчивых состояний автомата – это совокупность текущих значений физических параметров элементов памяти (например, напряжение на выходах триггеров), которая сохраняется до поступления соответствующего входного сигнала. Внутреннее состояние автомата соответствует некоторой памяти о прошлом и позволяет устранить время как явную переменную и выражать выходные сигналы в виде функции входов и памяти.

Автомат работает в дискретном времени и переход из состояния в состояние происходит мгновенно. По способу ввода дискретного времени автоматы подразделяются на синхронные и асинхронные. В синхронных автоматах дискретное время задают генератором синхросигналов: t= 0, 1, 2 …, где t – номер машинного такта. В асинхронных автоматах моменты перехода из одного состояния в другое предварительно не определены и зависят от некоторых событий. В таких автоматах интервал дискретности переменный.

В теории наиболее полно описаны и на практике широко применяются син­хронные автоматы. Автомат, имеющий начальное состояние, называется иници­альным. В начальный момент времени t = 0 инициальный автомат всегда находит­ся в начальном состоянии Z.

По способу формирования выходных сигналов различают автоматы Мили, Мура и С-автоматы. Функция переходов всех автоматов одинакова и записывается в виде:

Z(t) = 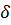[X(t), Z(t-1)].

Функции выходов задают выражения:

Y(t) = [X(t), Z(t-1)] – для автоматов Мили;

Y{t) = [Z(t)] – для автоматов Мура;

С-автомат объединяет свойства автоматов Мили и Мура.

Абстрактные автоматы Мили и Мура характеризуются одноканальными входами и выходами (рисунок 7.3.1).

Рисунок 7.3.1. Структура абстрактных автоматов Мили и Мура

 

Функция переходов 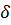показывает все возможные переходы из одного состояния памяти z_i в другое z_j, под действием входных сигналов. Функция выходов задает все возможные выходные сигналы, вырабатываемые автоматом в дискретные моменты времени в зависимости от x_i(t) и z_i (t).

В автоматах Мили выходные сигналы являются функцией входных сигналов и состояния памяти. В автоматах Мура выходные сигналы определяются только состоянием памяти.

Автомат называется конечным, если его множества X, Y и Z конечны; иначе автомат является бесконечным. В конечном автомате переход из одного состояния в любое другое заканчивается за конечное число тактов.

Принцип микропрограммного управления

Мы рассмотрели выполнение операций процессором в виде последо­вательности микрокоманд. Можно предусмотреть другой способ фор­мирования управляющих сигналов, под действием которых в операционном устройстве выполняются микрокоманды.

Управляющие сигналы у₁...., у_n на выходе управляющего устройства в каждом тактовом периоде имеют уровни лог. 0 и лог.1. Таким образом, каждой микрокоманде на выходе управляющего устройства соответствует некоторая кодовая комбинация. Такие кодовые комбинации, называемые кодовыми комбинациями микрокоманд (или просто микрокомандами), можно хранить в специально предназначенной для них управляющей памяти. При этом выполнение операции сводится к выборке из управляющей памяти последовательно микрокоманд микропрограммы и выдаче с их помощью управляющих сигналов у₁...., у_n в операционное устройство.

В управляющей памяти можно хранить много микропрограмм, пред­назначенных для выполнения различных операций. По выбранной из оперативной памяти команде в управляющей памяти находится соответствующая команде микропрограмма. Далее путем последовательного считывания микрокоманд найденной микропрограммы и их выполнения в операционном устройстве реализуется предусматриваемая командой операция. Такой способ реализации операций называется микропрограммным, а построенное на этом способе управляющее устройство – управляющим устройством с программируемой логикой. На рисунке 7.3.2 а) изображена структурная схема процессора с управля­ющим устройством, построенным по принципу программируемой логики.

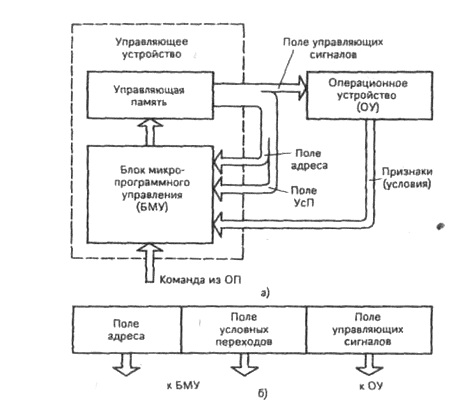
Рисунок 7.3.2.

Функции блока микропрограммного управления (БМУ) сводятся к определению адреса очередной микрокоманды (МК) в управляющей памяти (УП). Поступающая из оперативной памяти (ОП) команда содержит адрес первой МК той микропрограммы, которая реализует предусматриваемую командой операцию. Так решается задача поиска в УП микропрограммы, соответствующей данной команде. Адреса всех последующих МК определяются в БМУ следующим образом.

В формате МК (рисунок 7.3.2. б) предусматривается поле адреса, которое содержит адрес очередной МК. Считав из УП микрокоман­ду, по содержимому ее поля адреса определим адрес следующей МК. Но так можно получить адреса МК при отсутствии в алгоритме разветвлений, т.е. условных переходов (УсП). Для реализации условных переходов в МК надо предусмотреть поле условных пере­ходов, в котором указывается, имеет ли место условный или безус­ловный переход и при условном переходе – на значения каких условий следует ориентироваться при определении адреса очередной МК.

Пусть поле условных переходов построено следующим образом. Один из разрядов поля указывает вид перехода (например, 0 в этом разряде означает безусловный переход, 1 – условный переход). Кроме того, для каждого условия в поле условных переходов имеется разряд, указывающий участие данного условия в определении адреса. Если условный переход осуществляется по некоторому условию, то адрес очередной МК будем формировать замещением младшего разряда содержимого поля адреса текущей МК значением соответствующего ус­ловия (такую операцию называют модификацией адреса). Получается разветвление на два направления. В зависимости от значения условия образуются два различающихся в младшем разряде адреса и очередная МК считывается из одной либо другой ячейки УП. Если модифицировать два разряда содержимого поля адреса, то можно осуществить разветвление на четыре направления.

Поле управляющих сигналов МК используется для подачи управляющих сигналов в операционное устройство (ОУ).

Таким образом, микрокоманда может быть разбита на две части:

– одна часть – поле адреса и поле условных переходов – определяет функционирование БМУ при нахождении адреса очередной МК и может быть названа микрокомандой БМУ;

– другая часть – поле управляющих сигналов – определяет функционирование ОУ и может быть названа микрокомандой ОУ.