14) Полагая, что рост мужчин определенной возрастной группы есть нормально распределенная случайная величина X с параметрами a = 173 и σ = 6, найти долю костюмов 4-го роста (176 – 182 см), которые нужно предусмотреть в общем объеме производства для данной возрастной группы.
Решение
Доля костюмов 4-го роста (176 – 182 см) в общем объеме производства для данной возрастной группы определим по формуле:
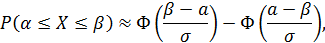
где 
– функция Лапласа,
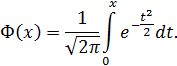
Из условия следует, что a = 173, σ = 6, α = 176, β = 182. Поэтому:
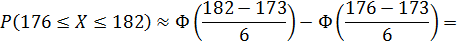
По таблице значений функции (см. приложение 2) определяем, что:
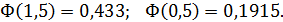
Значит:
Ответ: 
Вариационный ряд
15) Дана выборка значений некоторого непрерывного распределенного количественного признака Х, объем выборки n = 50:
| -2,25 | 0,38 | -1,31 | -1,05 | -0,07 | -4,17 | 3,69 | -1,47 | 2,34 | -1,22 |
| 0,42 | -3,24 | 0,95 | -0,68 | 0,15 | 1,75 | 0,71 | -3,37 | 0,95 | 0,99 |
| -3,1 | -2,79 | -1,15 | 2,26 | 0,21 | 1,37 | -1,62 | 1,41 | 3,95 | -1,05 |
| -0,03 | -2,49 | -0,52 | 2,91 | -5,71 | 0,91 | -3,78 | -0,14 | -0,82 | -2,4 |
| 3,78 | 1,17 | -1,79 | 0,16 | 2,02 | -3,88 | 0,64 | -1,08 | 3,18 | -0,84 |
Требуется:
1) Построить интервальный ряд, определив количество интервалов по формуле Стерджеса, рассчитать частоты, относительные частоты (частости), накопленные частоты, накопленные частости.
2) Построить гистограмму, кумуляту.
3) Найти средние величины: выборочное среднее, медиану, моду.
4) Найти показатели вариации: размах, среднее линейное отклонение, выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение, коэффициент вариации.
Решение
1) Построим интервальный ряд: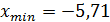 
; 
.
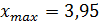Согласно формуле Стерджеса рекомендуемое число интервалов:
.
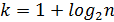Т.к. n = 50, то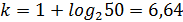 
. Будем считать k = 7. Начало первого интервала 
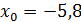. Конец последнего, седьмого интервала 
(минимальное и максимальное значение признака округлили в соответствующую сторону с точностью до десятых: для нижней границы – до десятых вниз, для верхней границы – до десятых вверх).
Длина каждого интервала будет равна[1]:
.
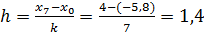Подсчитаем число вариант, попадающих в каждый интервал, получим вариационный ряд:
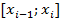
| [-5.8; -4.4) | [-4.4; -3) | [-3; -1.6) | [-1.6; -0.2) | [-0.2; 1.2) | [1.2; 2.6) | [2.6; 4) |
|
Разделив частоты на объем выборки найдем относительные частоты (частости):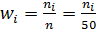 
; 
; 
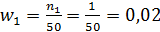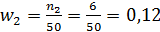и т.д.
Получаем:
|
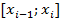
| [-5.8; -4.4) | [-4.4; -3) | [-3; -1.6) | [-1.6; -0.2) | [-0.2; 1.2) | [1.2; 2.6) | [2.6; 4) |
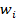
| 0,02 | 0,12 | 0,12 | 0,22 | 0,3 | 0,12 | 0,1 |
Запишем интервальный ряд с накопленными частотами[2]:
|
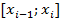
| [-5.8; -4.4) | [-4.4; -3) | [-3; -1.6) | [-1.6; -0.2) | [-0.2; 1.2) | [1.2; 2.6) | [2.6; 4) |
|
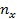
Накопленные частоты подсчитывали как количество вариант, значения которых меньше правой границы каждого интервала.
Запишем интервальный ряд с накопленными частостями:
|
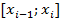
| [-5.8; -4.4) | [-4.4; -3) | [-3; -1.6) | [-1.6; -0.2) | [-0.2; 1.2) | [1.2; 2.6) | [2.6; 4) |
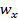
| 0,02 | 0,14 | 0,26 | 0,48 | 0,78 | 0,9 |
Накопленные частости рассчитывали по формуле: 
.
2) Построим гистограмму частот в MS Excel:
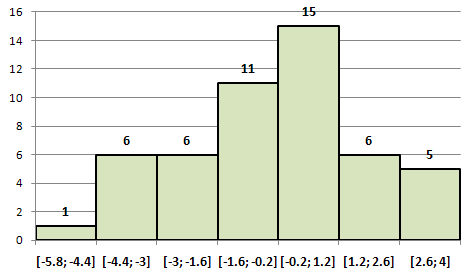
Построим кумуляту для интервального ряда – ломанную, которая начинается с точки, абсцисса которой равна началу первого интервала, а ордината – нулю; другие точки этой ломанной соответствуют концам интервалов и накопленным частотам. Воспользуемся средствами MS Excel:
3) Найдем средние величины.
Среднее выборочное:
Значения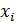 
– середины интервалов:
|
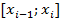
| [-5.8; -4.4) | [-4.4; -3) | [-3; -1.6) | [-1.6; -0.2) | [-0.2; 1.2) | [1.2; 2.6) | [2.6; 4) |
|
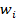
| 0,02 | 0,12 | 0,12 | 0,22 | 0,3 | 0,12 | 0,1 |
| середины интервалов | -5,1 | -3,7 | -2,3 | -0,9 | 0,5 | 1,9 | 3,3 |
.
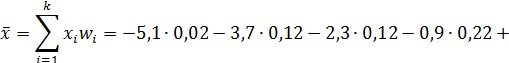
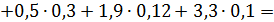
Таким образом, 
.
Найдем медиану интервального ряда – значение признака, приходящегося на середину ранжированного ряда наблюдений. Сначала определяем интервал медианы – первый интервал, в котором накопленная частота окажется больше половины объема выборки, т.е. больше 25.
|
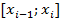
| [-5.8; -4.4) | [-4.4; -3) | [-3; -1.6) | [-1.6; -0.2) | [-0.2; 1.2) | [1.2; 2.6) | [2.6; 4) |
|
| |||||||
|
|
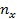
Таким интервалом в нашем случае является [-0.2; 1.2].
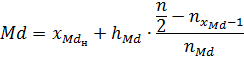
Таким образом,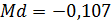 
.
Найдем моду интервального ряда – значение признака, которому соответствует наибольшая частота. Сначала определяем интервал моды – интервал с наибольшей частотой: [-0.2; 1.2].
|
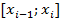
| [-5.8; -4.4) | [-4.4; -3) | [-3; -1.6) | [-1.6; -0.2) | [-0.2; 1.2) | [1.2; 2.6) | [2.6; 4) |
|
|
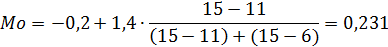
Таким образом,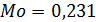 
.
4) Найдем показатели вариации.
Размах: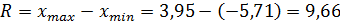 
.
Среднее линейное отклонение:
Значения 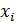– середины интервалов, 
.
|
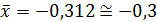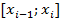
| [-5.8; -4.4) | [-4.4; -3) | [-3; -1.6) | [-1.6; -0.2) | [-0.2; 1.2) | [1.2; 2.6) | [2.6; 4) |
|
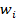
| 0,02 | 0,12 | 0,12 | 0,22 | 0,3 | 0,12 | 0,1 |
| середины интервалов | -5,1 | -3,7 | -2,3 | -0,9 | 0,5 | 1,9 | 3,3 |
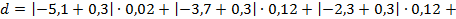
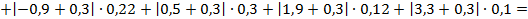
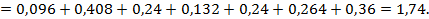
Таким образом,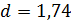 
.
Выборочная дисперсия:
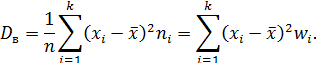
Значения 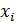– середины интервалов, .
|
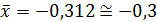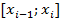
| [-5.8; -4.4) | [-4.4; -3) | [-3; -1.6) | [-1.6; -0.2) | [-0.2; 1.2) | [1.2; 2.6) | [2.6; 4) |
|
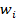
| 0,02 | 0,12 | 0,12 | 0,22 | 0,3 | 0,12 | 0,1 |
| середины интервалов | -5,1 | -3,7 | -2,3 | -0,9 | 0,5 | 1,9 | 3,3 |
.
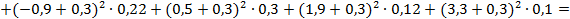
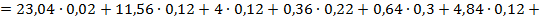
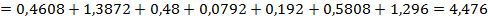Таким образом,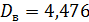 
.
Выборочное среднее квадратическое отклонение:
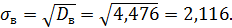
Коэффициент вариации:
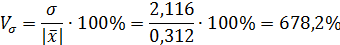
Исправленные выборочная дисперсия и среднее квадратическое отклонение:
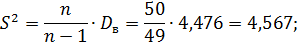
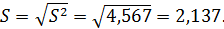
Ответ: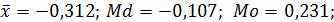 
Задания для контрольной работы
