ЛЕКЦИИ
Определение вероятности события
Классическое определение вероятности события. При классическом определении вероятность события определяется равенством
P (A)= m / n,
где m – число элементарных исходов испытания, благоприятствующих появлению события A; n – число возможных элементарных исходов испытания. Предполагается, что элементарные исходы образуют полную группу и равновозможны.
Геометрическое определение вероятности. Пусть отрезок l составляет часть отрезка L. На отрезке L наудачу поставлена случайная точка. Если предположить, что вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L, то вероятность попадания точки на отрезок l определяется равенством
P = Длина l /Длина L
Теорема сложения вероятностей
Теорема сложения вероятностей несовместных событий. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Р (А + В) = Р (А) + Р (В).
Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Р (А 1+ А 2+...+ Аn) = P (A 1) + Р (А 2) +…+ Р (Аn).
Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления
Р (А + В) = Р (А) + Р (В) – Р (АВ).
Теорема может быть обобщена на любое конечное число совместных событии. Например, для трех совместных событий
Р (A + В +С) = Р (А) + Р (В) + Р (С) – Р (АВ) – Р (АС) – Р (ВС) + Р (ABC).
Теорема умножения вероятностей
Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Р (АВ) = Р (А) ∙РA (В).
В частности, для независимых событий
P (АВ) = Р (А) ∙Р (В),
т. е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.
Формула полной вероятности
Вероятность события А, которое может наступить лишь при появлении одного из несовместных событий (гипотез) H 1, H 2, …, H n образующих полную группу, равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события A:
где 
.
Формула Байеса
Пусть событие А может наступить лишь при условии появления одного из несовместных событий (гипотез) H 1, H 2, …, Hn, которые образуют полную группу событий. Если событие А уже произошло, то вероятности гипотез могут быть переоценены по формулам Байеса
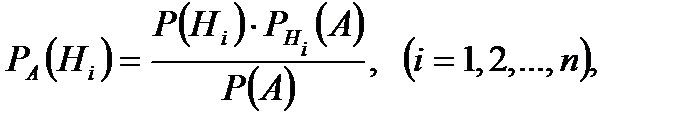
где 
Формула Бернулли
Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p (0 < p < 1), событие наступит ровно m раз (безразлично, в какой последовательности), равна
где 
q = 1 – p.
Вероятность того, что в n испытаниях событие наступит: а) менее m раз; б) более m раз; в) не менее m раз; г) не более m раз, находят соответственно по формулам:
Pn (0) + Pn (1) +…+ Pn (m – 1);
Pn (m + 1) + Pn (m + 2) +…+ Pn (n);
Pn (m) + Pn (m + 1) +…+ Pn (n);
Pn (0) + Pn (1) +…+ Pn (m).
Формула Пуассона
Если вероятность p наступления события A – постоянна и мала, а число испытаний n – велико и число λ = np – незначительно (будем полагать, что λ = np ≤ 10), то имеет место приближенное равенство:
Локальная и интегральная теорема Муавра-Лапласа
Локальная теорема. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р <1), событие наступит ровно m раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n)
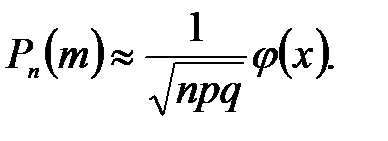
Здесь
, 
,
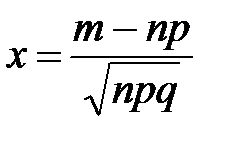Таблица значений функции Гаусса 
для положительных значений х приведена в приложении 1; для отрицательных значений х пользуются этой же таблицей с учетом того, что функция 
четная, следовательно,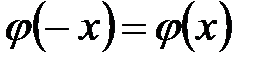 
.
Интегральная теорема. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит не менее m 1 раз и не более m 2 раз, приближенно равна
P (m 1; m 2) = Φ(x ¢¢) – Φ(x ¢)
Здесь 
– функция Лапласа,
Таблица значений функции Лапласа для положительных значений х (0 ≤ х ≤ 5) приведена в приложении 2; для значений х > 5 полагают Φ(x) = 0,5. Для отрицательных значений х используют эту же таблицу, учитывая, что функция Лапласа нечетная Ф(– x)= –Ф(x).
На практике, приближенные равенства из локальной и интегральной теоремы Муавра-Лапласа используют при выполнении условия: npq > 20.
