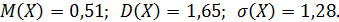10) Найти вероятность того, что событие A наступит ровно 70 раз в 200 независимых испытаниях, если вероятность появления этого события в каждом испытании равна 0,3.
Решение
Число испытаний: n = 200.
Число появлений события A: m = 70.
Вероятность появления события A: p = 0,3, значит q = 1 – p = 0,7.
Величина npq = 200∙0,3∙0,7 = 42.
Так как npq > 20, то можно воспользоваться приближенным равенством из локальной теоремы Муавра-Лапласа:
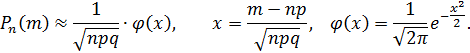
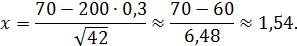
По таблице значений функций Гаусса (приложение 1) находим:
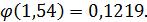
Тогда: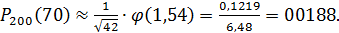 
Ответ: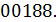 
11) Вероятность появления события A в каждом из 200 независимых испытаниях постоянна и равна 0,3. Найти вероятность того, что событие A появится не более 70 раз.
Решение
Число испытаний: n = 200.
Вероятность появления события A: p = 0,3, значит q = 1 – p = 0,7.
Величина npq = 200∙0,3∙0,7 = 42.
Так как npq > 20, то можно воспользоваться приближенным равенством из интегральной теоремы Муавра-Лапласа:
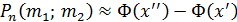, где
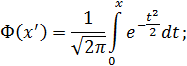
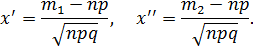
Необходимо найти вероятность того, что событие A появится не более 70 раз, а это значит, что число появлений события A принадлежит промежутку [0; 70], то есть m 1 = 0, m 2 = 70.
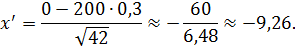
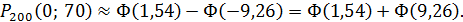
По таблице значений функций Лапласа (приложение 2) находим:
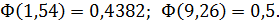
Ответ: 
12) Проведено 300 независимых испытаний с вероятностью появления события A в каждом из них 0,01. Найти вероятность того, что событие A появится точно 1 раз.
Решение
Число испытаний велико: n = 300.
Вероятность появления события A в каждом из них мала: p = 0,01.
Произведение λ = np = 300∙0,01 = 3 меньше 10, значит можно искомую вероятность найти по формуле Пуассона:
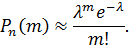
Необходимо найти вероятность того, что событие A появится точно 1 раз, значит m = 1:
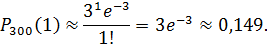
Значение 
можно вычислить в MS Excel, если ввести в любую ячейку формулу =Exp(–3) и нажать Enter.
Ответ: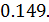 
Дискретные случайные величины
13) В денежной лотерее выпущено 100 билетов. Разыгрывается четыре выигрыша по 5 тысяч рублей; пять выигрышей по 4 тысячи рублей и одиннадцать выигрышей по 1 тысячи рублей.
а) Составить ряд распределения случайной величины X – размер выигрыша по одному купленному билету.
б) Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины.
в) Записать функцию распределения и построить ее график.
Решение
а) Случайная величина X – размер выигрыша по одному купленному билету.
Возможные значения случайной величины:
0; 1; 4; 5.
Вероятность выиграть 5 тысяч рублей по одному билету:
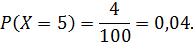
Аналогично определяются вероятности остальных значений случайной величины.
Ряд распределения имеет вид:
| X | ||||
| p | 0,8 | 0,11 | 0,05 | 0,04 |
б) Найдем числовые характеристики случайной величины.
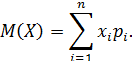
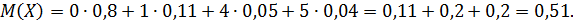
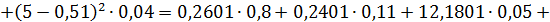
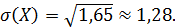
в) Найдем функцию распределения случайной величины F (x).
По определению: F (x) = P (X < x).
1) Пусть x = 0, найдем F (x):
F (0) = P (X < 0),
то есть вероятность того, что выигрыш по лотерейному билету будет меньше нуля, но это невозможное событие, значит P (X < 0) = 0 и F (0) = 0.
Очевидно, что для всех чисел из промежутка (–∞; 0] значение функции распределения будет таким же:
x ≤ 0: F (x) = 0.
2) Пусть x = 1, найдем F (x):
F (1) = P (X < 1),
то есть вероятность того, что выигрыш по лотерейному билету будет меньше 1, т.е. выигрыш будет равен нулю:
F (1) = P (X < 1) = P (X = 0) = 0,8.
Очевидно, что для всех чисел из промежутка (0; 1] значение функции распределения будет таким же:
0 < x ≤ 1: F (x) = 0,8.
3) Пусть x = 4, найдем F (x):
F (4) = P (X < 4),
то есть вероятность того, что выигрыш по лотерейному билету будет меньше 4, значит выигрыш равен нулю или равен 1 т.р.:
F (4) = P (X < 4) = P (X = 0) + P (X = 1) = 0,8 + 0,11 = 0,91.
Очевидно, что для всех чисел из промежутка (1; 4] значение функции распределения будет таким же:
1 < x ≤ 4: F (x) = 0,91.
4) Пусть x = 5, найдем F (x):
F (5) = P (X < 5),
то есть вероятность того, что выигрыш по лотерейному билету будет меньше 5, значит равен нулю или 1 т.р. или 4 т.р.:
F (5) = P (X < 5) = P (X = 0) + P (X = 1) + P (X = 4) =
= 0,8 + 0,11 + 0,05 = 0,96.
Очевидно, что для всех чисел из промежутка (4; 5] значение функции распределения будет таким же:
4 < x ≤ 5: F (x) = 0,96.
5) Пусть x > 5, например, x = 6; найдем F (x):
F (6) = P (X < 6),
то есть вероятность того, что выигрыш по лотерейному билету будет меньше 6, а это достоверное событие – в любом случае выигрыш будет меньше 6 т.р. (возможные значения 0; 1; 4; 5), поэтому:
F (6) = 1.
Очевидно, что для всех чисел больших 5, то есть из промежутка (5; +∞) значение функции распределения будет таким же:
x > 5: F (x) = 1.
Получаем:
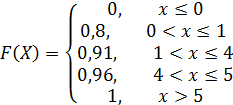
Построим ее график:
Ответ: 
