На первый взгляд может показаться, что для задания дискретной случайной величины достаточно перечислить все ее возможные значения. В действительности это не так: случайные величины могут иметь одинаковые перечни возможных значений, а вероятности их — различные. Поэтому для задания дискретной случайной величины недостаточно перечислить все возможные ее значения, нужно еще указать их вероятности.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.
При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая — их вероятности:
X xt xt... хп
Р Pi Pt '•• Рп
Приняв во внимание, что в одном испытании случайная величина принимает- одно и только одно возможное значение, заключаем, что события X — xlt X = xa,..., X = хп образуют полную группу; следовательно, сумма вероятностей этих событий, т. е. сумма вероятностей второй строки таблицы, равна единице:
Если множество возможных значений X бесконечно (счетно), то ряд р1-\-р1 +... ходитсяс и его сумма равна единице.
Пример. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 руб. и десять выигрышей по 1 руб. Найти закон распределения случайной величины X — стоимости возможного выигрыша для владельца одного лотерейного билета'. Решение. Напишем возможные значения X: *1 = 50, хг—\, х3 = 0. Вероятности этих возможных значений таковы: р1 = 0,01, р„ = 0,01, Рз=1-(р1 + Р4)=0,89.
Напишем искомый закон распределения:
X 50 10 0
р 0,01 0,1 0,89
14. Система двух непрерывных случайных величин: функция распределения и ее свойства, функции распределения случайных величин, входящих в систему.
Как уже отмечалось, дискретная случайная величина может быть задана перечнем всех ее возможных значений и их вероятностей. Такой способ неприменим для непрерывных случайных величин, так как невозможно составить перечень всех возможных значений, заполняющих интервал (a,b). В связи с этим вводится понятие функции распределения вероятностей случайной величины, пригодное как для дискретной, так и для непрерывной случайной величины.
Пусть x – действительное число. Вероятность события, состоящего в том, что X примет значение, меньшее x, т.е. вероятность события 
, обозначим через 
. Разумеется, если x изменяется, то, вообще говоря, изменяется и , т.е. есть функция x.
Функцией распределения называют функцию , определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее x:
Геометрически это равенство можно истолковать так: есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее x.
Рассмотрим по-отдельности случаи дискретной и непрерывной случайной величин.
1. Дискретная случайная величина. Рассмотрим функцию распределения 
дискретной случайной величины 
, принимающей значения 
.
ü Если 
, то 
, так как в этом случае событие 
является невозможным.
ü Если 
, то событие наступит тогда и только тогда, когда наступит событие 
, поэтому 
.
ü Если 
, то событие равно сумме событий 
и 
и
.
ü Аналогично, если 
, то 
.
Таким образом, функция распределения случайной дискретной величины равна 
, где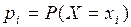 
, и суммирование производится по тем 
, для которых 
.
Таким образом, в точках функция распределения испытывает скачки.
2. Непрерывная случайная величина. В отличие от случая дискретной случайной величины в данном случае пробегает все непрерывное множество значений, а сама функция 
возрастает монотонно.
Если вероятность события 
равна 
, а вероятность события 
равна 
, то вероятность того, что случайная величина заключена между 
и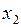 
равна разности соответствующих значений функции распределения: 
.
Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю. Имеет смысл рассматривать лишь вероятность попадания ее в некоторый интервал, пусть даже и сколь угодно малый.
График функции распределения для дискретной случайной величины представляет собой ступенчатую разрывную функцию, а непрерывной –монотонно возрастающую непрерывную функцию.
Пример. Пусть среднедушевой доход в у.е. описывается функцией распределения
где 
. Какова вероятность того, что в случайно выбранной семье среднедушевой доход меньше 200 у.е.? Вероятность того, что среднедушевой доход лежит в пределах от 50 до 150 у.е.? Ответ: а) 
, б) 0,534.
