РАЗДЕЛ 5. ЭКСТРЕМУМЫ
· Излагаются вопросы исследования функций на экстремум
· Рассматриваются экстремумы функций одной и нескольких переменных
МОНОТОННОСТЬ ФУНКЦИИ. ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА ФУНКЦИИ
Напомним основные определения.
Определение. Функция  , определенная на промежутке
, определенная на промежутке  , возрастает на этом промежутке, если для любых
, возрастает на этом промежутке, если для любых  ,
,  имеет место неравенство
имеет место неравенство  .
.
Функция  , определенная на промежутке
, определенная на промежутке  , не убывает на
, не убывает на  , если для любых
, если для любых  ,
,  имеет место неравенство
имеет место неравенство 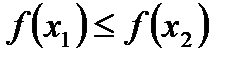 .
.
Функция  , определенная на промежутке
, определенная на промежутке  , убывает на
, убывает на  , если для любых
, если для любых  ,
,  имеет место неравенство
имеет место неравенство  .
.
Функция  , определенная на промежутке
, определенная на промежутке  , не возрастает на
, не возрастает на  , если для любых
, если для любых  ,
,  имеет место неравенство
имеет место неравенство  .
.
Общее название рассмотренных функций - монотонные функции.
Ясно, что если функция возрастает на  , то она, тем более, не убывает на
, то она, тем более, не убывает на  (но не наоборот). Аналогичное замечание справедливо для убывающей функции.
(но не наоборот). Аналогичное замечание справедливо для убывающей функции.
Общее название возрастающих, убывающих функций – строго монотонные функции.
Теорема. Пусть функция  дифференцируема на интервале
дифференцируема на интервале  . Она не убывает (не возрастает) на
. Она не убывает (не возрастает) на 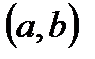 тогда и только тогда, когда для всех
тогда и только тогда, когда для всех  выполняется неравенство
выполняется неравенство  .
.
◄Пусть  не убывает на
не убывает на 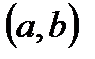 (случай невозрастания рассматривается аналогично). Тогда рассмотрим произвольную точку
(случай невозрастания рассматривается аналогично). Тогда рассмотрим произвольную точку  и приращения
и приращения  такие, что
такие, что 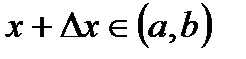 . Если
. Если  , то
, то  и
и  .
.
Если  , то
, то 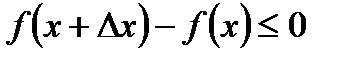 , но все равно
, но все равно  . Предел
. Предел  существует и равен
существует и равен  . По теореме о предельном перехоле в неравенстве этот предел
. По теореме о предельном перехоле в неравенстве этот предел  .
.
Обратно пусть для всех 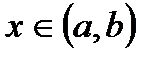 выполняется неравенство
выполняется неравенство  . Пусть
. Пусть  ,
,  . К отрезку
. К отрезку  можно применить теорему Лагранжа. Действительно, т.к.
можно применить теорему Лагранжа. Действительно, т.к.  дифференцируема на
дифференцируема на  , то она непрерывна на
, то она непрерывна на  , а, значит, и на
, а, значит, и на  . Также по условию она дифференцируема на
. Также по условию она дифференцируема на  . Следовательно,
. Следовательно, 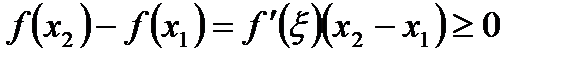 .►
.►
Теорема допускает уточнение
Теорема. Пусть  дифференцируема на
дифференцируема на  и для всех
и для всех 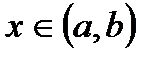 выполняется неравенство
выполняется неравенство  . Тогда
. Тогда  возрастает на
возрастает на  .
.
◄Как и в предыдущей теореме, получаем, что для любых  ,
,  , имеет место неравенство
, имеет место неравенство
 .►
.►
Замечание. Утверждать, что если функция возрастает, то для всех  выполняется неравенство
выполняется неравенство  нельзя. Пример функции
нельзя. Пример функции  показывает, что хотя эта функция возрастает на всей прямой, есть точка
показывает, что хотя эта функция возрастает на всей прямой, есть точка  , в которой ее производная равна 0.
, в которой ее производная равна 0.
Таким образом, даже возрастание функции  гарантирует, по теореме 29.1, лишь нестрогое неравенство
гарантирует, по теореме 29.1, лишь нестрогое неравенство  .
.
В теореме Ферма установлено необходимое условие экстремума: Если функция  имеет производную
имеет производную  в точке экстремума
в точке экстремума  , то
, то  .
.
Как показывает пример из предыдущего замечания, 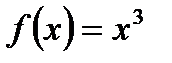 , это условие не является достаточным.
, это условие не является достаточным.
Теорема. Пусть функция  непрерывна в некоторой окрестности
непрерывна в некоторой окрестности  и пусть
и пусть  для всех
для всех  и
и 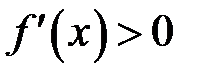 для всех
для всех  . Тогда
. Тогда  -точка минимума. Если же
-точка минимума. Если же 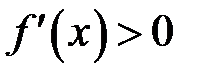 для всех
для всех  и
и 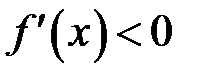 для всех
для всех  , то
, то 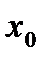 - точка максимума.
- точка максимума.
◄Проведём доказательство для точки минимума. Пусть  , и
, и  .
.
Если 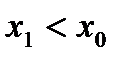 , то применим теорему Лагранжа к отрезку
, то применим теорему Лагранжа к отрезку  :
:
 .
.
Если  , то применим теорему Лагранжа к отрезку
, то применим теорему Лагранжа к отрезку  :
:
 ,
,
Поэтому  . Таким образом,
. Таким образом,  - точка минимума.►
- точка минимума.►
Теорема. Пусть  ,
,  существует в
существует в  и
и  . Пусть
. Пусть  такова, что
такова, что  ,
, 
Тогда если  , то
, то  - точка максимума, если
- точка максимума, если  , то
, то 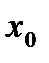 - точка минимума.
- точка минимума.
◄Условия теоремы дают возможность применить формулу Тейлора с остаточным членом в форме Пеано, согласно которой, с учётом равенства  , имеем:
, имеем:
 , где
, где  при
при  .
.
Пусть  . Так как
. Так как  при
при  , существует
, существует  такое, что для любых
такое, что для любых  :
: 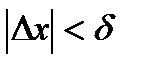 выполняется неравенство
выполняется неравенство  .
.
Это означает, что модуль второго слагаемого в сумме  не превосходит половины модуля первого слагаемого, т.е.
не превосходит половины модуля первого слагаемого, т.е. 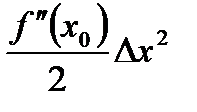 , поэтому знак этой суммы совпадает со знаком
, поэтому знак этой суммы совпадает со знаком  . Но знак этой величины совпадает со знаком
. Но знак этой величины совпадает со знаком  как при
как при  , так и при
, так и при  , так как
, так как  . Следовательно, приращение
. Следовательно, приращение  не меняет знак в окрестности точки
не меняет знак в окрестности точки  , и знак его совпадает со знаком
, и знак его совпадает со знаком  . Это и означает, что если
. Это и означает, что если  , то
, то 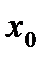 - точка максимума, а если
- точка максимума, а если 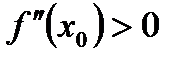 , то
, то 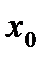 - точка минимума.►
- точка минимума.►
Ещё более тонкий достаточный признак экстремума содержится в следующей теореме.
Теорема. Пусть  ,
,  существует в
существует в  и
и 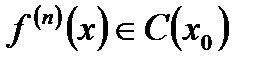 . Пусть точка
. Пусть точка  такова, что
такова, что  , а
, а 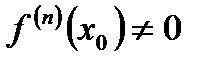 . Тогда если n – чётное число, то в точке
. Тогда если n – чётное число, то в точке  есть экстремум, минимум при
есть экстремум, минимум при  , максимум при
, максимум при  .
.
Если же n – нечётное число, то в точке  экстремума нет.
экстремума нет.
◄Аналогично предыдущей теореме, получаем равенство  , где
, где 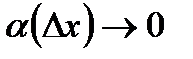 при
при  , из которого точно так же следует, что знак приращения
, из которого точно так же следует, что знак приращения  совпадает со знаком
совпадает со знаком  при условии
при условии  .
.
Если n – чётное число, то, как и в предыдущей теореме,  как для
как для  , так и для
, так и для  , поэтому знак приращения совпадает со знаком
, поэтому знак приращения совпадает со знаком  и заключение теоремы становится очевидным.
и заключение теоремы становится очевидным.
Если же n – нечётное число, то величина  положительна при
положительна при  и отрицательна при
и отрицательна при  , поэтому приращение
, поэтому приращение  меняет свой знак в произвольной окрестности точки
меняет свой знак в произвольной окрестности точки  , следовательно, в точке
, следовательно, в точке 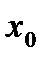 нет экстремума. ►
нет экстремума. ►






