Практикалық сабақ 11 Анықталмаған интеграл және интегралдаудың негізгі әдістері

Есеп 1.

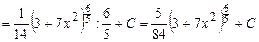
Есеп. .

Есеп.

Есеп. .

Есеп.

Есеп. Есепте

Ауыстыру арқылы Онда , , ның орына .Онда

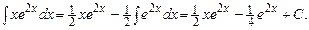
Есеп. Есепте

Полагаем 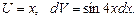Тогда , , и в качестве можем взять . Следовательно

.

Есеп. Вычислить .

Бөліктеп и нт егралдау . Тогда , и поэтому . с , имеем . Онда

.

Есеп. Есепте .

 

2 және 3 ең кіші ортақ еселегі 6. Онда ауыстыру еңгіземіз 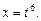Онда және .

Есеп. Есепте ауыстыру арқылы . Онда , және . Онда,

.

Есеп

Әдебиеттер

Ефимов А. В., Демидович Б. П. Сборник задач по математике, ч. 1, 2. М., «Наука», 1986, (с. 322-334)

Бақылау сұрақтар

1. Интегралдардың кестесі.
2. Бөлшектеп интегралдау формуласы.
3. Дифференциалға еңгізу.
4. Дифференциал және оның қасиеттері.

Практикалық сабақ 12 Рационал функцияны интегралдау

Есеп. Есепте .

Бөлімінің түбірлері – , и . Онда және рационалдық функцияны жиктеуге болады

.

Ортақ бөлімге келтіргенде

.

Коэффициенттерін жинағанда

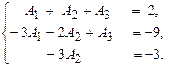
Табамыз .

Сонда,

.

Есеп Есепте .

Бөлімінің түбірлері – 1 еселі и 3еселі. Онда бөлшекті жіктейміз

.

Орьақ бөлімге келтіргенде

.

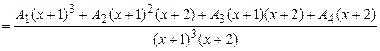Жақшаны ашқанда

.

Сонда,

.

Әдебиеттер

Ефимов А. В., Демидович Б. П. Сборник задач по математике, ч. 1, 2. М., «Наука», 1986, (с. 335-336)

1. Рационал бөлшекті қарапайым бөлшектерге жиктеу 1 жағдай.
2. Рационал бөлшекті қарапайым бөлшектерге жиктеу 2 жағдай.
3. Рационал бөлшекті қарапайым бөлшектерге жиктеу 3 жағдай.

Практикалық сабақ 13 Тригонометриялық және иррационал функцияларды интегралдау

Есеп. 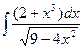Ауыстыру арқылы есептейміз. Онда дифференциал , және жанадан интеграл . Сонда

.

Есеп. Ауыстыру арқылы есептейміз. Онда Жанадан интеграл . Сонда,

.

Есеп. . Ең кіші ортақ еселегі 2 және 4 ол 4 тең. Сондықтан ауыстыру еңгіземіз Онда және

Пример.

Есепте

Есеп. .

Бірінші жағдайға келеді. Мұндағы дәрежесі тақ сан.Интеграл астындағы функцияға ауыстыру еңгіземіз . Онда дифференциал 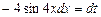, Онда

.

Есеп. .

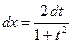МЫна интегралды универсалдық ауыстыру арқылы есептейміз . Онда , , , Интегралға қойғанда

.

Есеп Интегралды есепте .

Төртінші жағдайға келеді и Интегралға ауыстыру еңгіземіз . Тогда 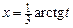, , . Интегралға қойғанда болады

Әдебиеттер

Ефимов А. В., Демидович Б. П. Сборник задач по математике, ч. 1, 2. М., «Наука», 1986, (с.340-344)

Бақылау сұрақтар

 

1. Универсалдық қай жағдайда еңгізеді?
2. Дәрежелері жұп болса қандай әдісемнен шешеді.
3. Ең болмағанда біреуі тақ болса қандай әдісемен шешеді?
4. Тригонометриялық ауыстыруыны қай жағдайларда пайдаланамыз.

Практикалық сабақ 14 Анықталған интеграл. Анықталған

Есеп. Бірінші жағдай .

Мысал. .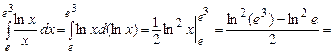

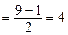Мысал.. .

Мысал. Есепте . Ауыстыру ,

. Онда бөлшектеп формуласын пайдаланып

.

Мысал. Есепте . Ауыстыру ,

. Онда және бөлшектеп формуласын пайдаланып

.

Мысал. Есепте Ауыстыру Онда ,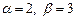

 

.

Мысал. Жинақтылығын зертте .

Есептегенде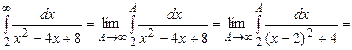

. Онда интеграл жинақты болады

Әдебиеттер

Ефимов А. В., Демидович Б. П. Сборник задач по математике, ч. 1, 2. М., «Наука», 1986, (с.344-354)

1. Ньютона-Лейбница формуласы.
2. Ауыстыру арқылы интегралдау.
3. Бөліктеп интегралдау.