сандарынан құрылған сандар жиынын 
тізбегінің мәндерінің жиыны дейді.
Анықтама. Белгілі бір С нақты саны және барлық нөмірлері үшін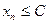 
теңсіздігі орындалатын тізбегін жоғарыдан шенелген тізбек деп атайды.
Анықтама. Белгілі бір С нақты саны және барлық нөмірлері үшін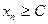 
теңсіздігі орындалатын тізбегін төменнен шенелген тізбек деп атайды.
Анықтама. Жоғарыдан да, төменнен де шенелген тізбекті шенелген тізбек деп атайды.
Анықтама. тізбегі берілсін. Егер әрбір n (n=1,2,...) үшін 
болса, онда оны кемімейтін тізбек деп, ал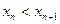 
болса, онда оны өспелі тізбек деп атайды.
Анықтама. тізбегі берілсін. Егер әрбір n (n=1,2,...) үшін 
болса, онда оны өспейтін тізбек деп, ал 
болса, онда оны кемімелі тізбек деп атайды.
Өспелі және кемімелі тізбектерді қатаң монотонды тізбек деп атайды.
Функция және оның шегі.
Е және Ғ жиындары берілсін. Е жиынының әрбір элементіне Ғ жиынының элементін сәйкес қоятын ереже функция деп аталады. Функция көбінесе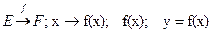 
символдарымен белгіленеді.Е-функцияның анықталу жиыны, Ғ – мәндерінің жиыны деп аталады.
Мтылғандағы функцияның шегі.
Анықтама. Егер белгілі бір А нақты саны мен кез келген 
оң саны үшін барлық x>N сандары үшін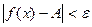 
теңсіздігі орындалатын N саны табылса, онда f(x) функциясының 
ұмтылғанда нақты мәнді шегі бар және ол А санына тең дейді де 
символымен белгілейді.
Анықтама. Егер кез келген мейлінше аз оң саны үшін N номері табылып,.
Анықтама. Егер а санына жинақталатын кез келген тізбегі үшін f функциясы мәндерінің сәйкес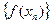 
А санына жинақтылатын болса, онда А санын f функциясының шегі деп атайды х а-ға ұмтылғанда
А= 
Анықтама. Егер 
тізбегінің шегі 0-ге тең болса, онда ол ақырсыз кіші тізбек деп аталады (
)
Анықтама. Егер тізбегінің шегі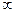 
-ге тең болса, онда ол ақырсыз үлкен тізбек деп аталады (
)
Қасиеті. Егер ақырсыз үлкен болса, онда 
ақырсыз кіші тізбек болады.
Функция шектері тұралы касиеттері.
1. Егер және 
шектері бар болса, онда 
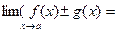
тендік орындалады.
2. Егер және шектері бар болса, онда 
тендік орындалады.
3. Егер және 
шектері бар болса, онда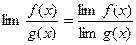 
тендік орындалады.
4. Егер бар болса, онда кез келген с саны үшін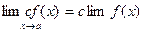 
тендік орындалады.
Теорема 1. Егер 
және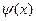 
функциялары құрдым аз функциялар болса, онда олардың қолданулары 
-да құрдым аз функция болады.
Теорема 2. Егер y=f(x) функциясының ұмтылғанда шегі бар болса, онда ол кез келген 
интервалында шенелген болады.
Теорема 3. Егер y=f(x) функциясының () нөлге тең емес шегі болса, онда 
функциясы шенелген болады.
Теорема 4. Құрдым аз функцияның шенелген функцияға көбейтіндісі құрдым аз функция болады.
Салдар. Құрдым аз функцияның санға көбейтіндісі құрдым аз функция болады.
Теорема 5. 
-да құрдым аз f(x) функциясын, шегі нөлге тең емес функциясына () бөлгенде шығатын функция құрдым аз функция болады.
