Практикалық сабақ 9 Функцияның экстремумы. Негізгі теоремалары. Функцияның ең үлкен және ең кіші мәндері

1 Есеп. Функцияның өсу және кему аралықтарын тап

Шешімі. Анықталу облысы

Туындысын табамыз Теңдеуді шешемі , , Туындының таңбасын анықтаймыз осы аралықта бірінші ретті туындысыоң болады Ал аралықта теріс болады Онда аралықта функция өседі. Ал аралықты функция кемиді.

2 Есеп. Функцияның экстремумдарын тап

Шешімі. Анықталу облысы

Туындысын табамыз Теңдеуді шешемі , , Туындының таңбасын анықтаймыз осы аралықта бірінші ретті туындысыоң болады Ал аралықта теріс болады Онда аралықта функция өседі. Ал аралықты функция кемиді

Онда максимум нүктесі минимум нүктесі.

3 Есеп. Функцияның , аралықта ең ұлкен және ең кіші мәдерін тап

Шешімі. Туындысын табамыз Теңдеуді шешемі , , - кризистік нүктелері Енді функция мәндерін есептейміз

Сонымен ең ұлкен мәні 2 тең, және ең кіші мәні -4 тең.

Әдебиеттер

Ефимов А. В., Демидович Б. П. Сборник задач по математике, ч. 1, 2. М., «Наука», 1986, (с.248-258)

Бақылау сұрақтар

1. Функцияның кризистік нүктелері

2. Өсу кему аралықтары

3. Экстремум Максимум жіне минимум

Практикалық сабақ 10 Функцияны ойыс және дөнес аралықтарға зерттеу. Иілу нуктелері. Асимптоталар. Функцияны толық зерттеу

1 Есеп. Функцияны зерттеу керек Грфигін салу керек

1) Анықталу облысы (-¥; -1) È (-1; 1) È (1; ¥). Мәндері облысы (-¥; ¥). Үзіліс нүктелері х = 1, х = -1.

2) Функия тақ болады, графигі (0,0) нүктесіне қатысты симмтериялы болады

3) Бірінші ретту туындының кризистік нүктелері табамыз

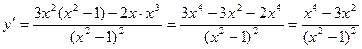Кризистік нүктелері: x = 0; x = - ; x = ; x = -1; x = 1.

4) Екіншщі ретті туындының кризистік нүктелерін табамыз

. x = -1; x =1; х=0

5) Кесте

х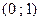
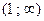
у		-		-		+
		-		+		+
		Кемийді және дөнес		Кемийді және ойыс		Өспелі және дөнес

 

Мүндағы х = - максимум нүктесі болады, ал х = минимум. Функция мәндері сәйкес -3 /2 и 3 /2.

6) х = 1, х = -1 түзулері вертикаль асимптоталар болады.

Көлбеу асимтотасын табамыз.

Көлбеу асимптотасы – y = x.

7) Координаттық өсьтерімен қиылысу нүктесі (0, 0)

8) Функцияның графигі:

 

Есеп. Функциянфң ойыс және дөнес аралықтарын тап Шешімі, Т, уындыларын табамыз . нүктесінде шексіздікке тең Сондақтан ол кризистік нүктесі Мұнда болса, онда екінші ретті туындысы , ал болса, аралықта функция дөнес болады, ал – ойыс Сондықтан – иілу нүктесі.

Есеп. Фукцияны иілу нүктесіне зерттеу керек.

Шешімі. Функция определена при , то есть на . Екінші және бірінші ретті туындыларды табамыз:

.

Екінші ретті туындысы барлық нүктелерде , онда барлық анықталу облысынды функция дөнес болады және иілу неұктелері жоқ.

Есеп. Функцияның асимптоталар тап .

Шешімі. , Сондықтан вертикал асимптотасы.

Есеп. Горизонтал асимптотасын тап .

Шешімі. Шекті есептейміз , яғни егер и при 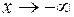, сондықтан – горизонтал асимптота болады

Әдебиеттер

Ефимов А. В., Демидович Б. П. Сборник задач по математике, ч. 1, 2. М., «Наука», 1986, (с.261-267)

Бақылау сұрақтар

1. Что такое выпуклость и вогнутость функции. Точки перегиба.
2. Условия существования точек перегиба.