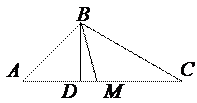Мысал.. Үшбұрыштың төбелері берілген 
, 
, 
. Табу керек
а) 
қабырғаның теңдеуі;
б) 
- медиананың теңдеуі;
в) 
- биіктігінің теңдеуі;
г) 
төбесінен биссектрисаның теңдеуі
Шешімі. а)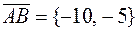 
векторды табамыз. Онда 
бағыттауыш векторы Онда ның канондық теңдеуі: 
, 
, немесе 
.
б) 
– 
-ның ортасы, онда 
, ал 
векторы бағыттауыш векторы. медиананың теңдеуі: немесе 
.
в) және перпендикуляр болғандықтан, онда нормаль 
. По формуле (2) получим: 
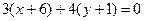немесе 
.
Мысал.. Берілген квадраттың екі қабырғасы 
и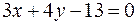 
. Ауданы есепете.
Шешімі. Екіқабырғаның арасындағы қашықтығын табамыз 
, :
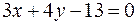. Тогда 
.
Мысал. 
нүктесіне 
түзуіне қатысты симметриялық нүктесін тап.
Шешімі. 
түзуді мыеа түрінде жазамыз 
, одан 
нормаль веторы 
. Онда канондық теңдеуі : 
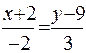. Жазықтықтын және түзідің қиылысу нүктесін табамыз и 
: 
, 
,
. Онда А нүктенің координатталары мына формуламен есептеледі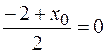 
, 
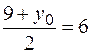, откуда 
, 
.
Мысал. Трапецияның төбелері берілген 
: 
. Қабырғалардың теңдеулерін тап
Шешімі. 
және 
нүктелерінің координтталары белгілі болғандықтан,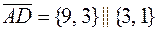 
табамыз, онда 
теңдеуі: 
немесе 
, нормалі 
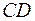түзудің бағытталған векторы, онда 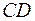түзудің теңдеуі 
немес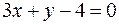е 
. 
және параллель болғандықтан, онда нормаль, теңдеуі 
немесе 
. Ал теңдеуді екі нүктедент өтетін арқылы формуласымен жазуға болады: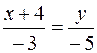 
немесе 
.
Әдебиет
Ефимов А. В., Демидович Б. П. Сборник задач по математике, ч. 1, 2. М., «Наука», 1986, (с.79-90)
Бақылау сұрақтар:
- Теңдеудін жалпы теңдеуі
- Екі нүктеден өтетін түзудің теңдеуі.
- Бұрыштық коэффициенттінің формуласы?
- Берілген қатысты бойынша кесендіні бөлу.
- Параллель және перпендикуляр түзулердің.
Практикалық сабақ 4 Кеңістіктегі аналитикалық геометрия
Мысал. 
нүктесінен өтетін және екі векторға параллель болатын 
және 
.
Шешімі. Кез келген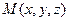 
нүктесін аламыз және 
нүктесімен қосып 
векторды табамыз.
, 
және 
компланар болғандықтан,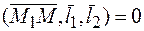 
. Одан
, немесе жалпы түрінде, 
.
Мысал.. Канондық және параметрлік теңдеуді жаз 
Шешімі. 
болсын, онда 
одан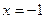 
, 
. 
берілген.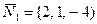 
, 
, 
, 
. Канондық теңдеуі: 
. Одан 
, теңістіріп парметрлік теңдеуі: 
, 
, 
.
Мысал. 
және 
түзулері бір жазықтықта жатама.
Шешімі. Бағытылған векторлары белгілі 
, 
, 
, 
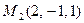, онда Егер векторлары бір жазықтықты жататын болса онда 
компланар болады 
.
, Онда түзулер бір жазықтықта жатпайды.
Әдебиетт
Ефимов А. В., Демидович Б. П. Сборник задач по математике, ч. 1, 2. М., «Наука», 1986, (с.111-123)
Бақылау сұрақтар:
- Жазықтықтың жалпы теңдеуі. Норомалі
- Үш нүктеден өтетін жазықтықтын теңдеуі.
- Нүктеден жазықтыққа дейінгі қашықтық.
- Кеңістіктегі түзудің алпы теңдеуі.
- Түзудің параметрлік теңдеуі.
Практикалық сабақ 5 Математикалық анализге кіріспе. Тізбектін шегі. Функцияның шегі.
Есеп. Есепте 
.
Шешімі. Мұндағы анықталмағандық 
. 
, так как 
, 
, 
при 
.
Есеп. Есепте 
.
Шешімі. Мұндағы анықталмағандық 
.
.
.
Мысал. 
. 
.
Мысал.
.
Әдебиеттер
Ефимов А. В., Демидович Б. П. Сборник задач по математике, ч. 1, 2. М., «Наука», 1986, (с.9-30)
Бақылау сұрақтар
- Анықталмандықтар дегеніміз не.
- Анықталмағандықтардың типтері.
- Ақырсыз кіші және ақырсыз үлкен функциялардың қасиеттері.
- Шектердің типтері.
