1-Анықтама. [a,b] сегментінде (немесе (а,в) интервалында) анықталған y=f(x) функциясы сол сегментте өспелі деп аталады, егер сол сегментте жатқан 
және 
нүктелері үшін, 
теңсіздігі үшін 
теңсіздігі орындалатын болса.
2-Анықтама. Егер 
нүктелері үшін 
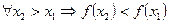болса, онда y=f(x) функциясы кемімелі деп аталады.
1-Теорема. (Функцияның монотондылық белгісі).
f(x) функциясы (а,в) интервалында дифференциалданатын болсын. Егер (а,в) интервалында 
болса, онда f(x) функциясы сол аралықта бірқалыпты өседі. Ал егер 
, болса онда f(x) бірқалыпты кемиді.
Функцияның ең үлкен және ең кіші мәндерінің анықтамалары.
1-Анықтама. f функциясы 
нүктесінің бір аймағында анықталсын. Сонда нүктесі f функциясының максимум (сәйкес минимум нүктесі) деп аталады, егер кез келген х үшін 
шартын қанағаттандыратын 
саны табылып 
(сәйкес 
) теңсіздігі орындалса. Онда нүктесі қатаң максимум нүктесі деп (сәйкес қатаң минимум нүктесі) аталады. Максимум және минимум нүктелері экстремум нүктелері деп аталады.
Теорема. (Экстремумның қажетті шарттары).
нүктесі сол нүктенің маңайында анықталған f функциясының экстремум нүктесі болсын. Сонда туынды 
болмайды немесе 
болады.
Теорема.( Экстремумның бар болуының жеткілікті белгісі).
f(x) функциясы кризистік 
нүктесінің 
маңайында үзіліссіз болып, оның ойылған маңайында дифференциалдансын ( нүктесінен басқа нүктелерде) және аргумент кризистік 
нүктесінен солдан оңға қарай өткенде туынды 
таңбасын «+» тан «-» қа ауыстырса онда функция сол нүктеде максимумға жетеді, ал таңбасын «-» тан «-» қа ауыстырса минимумға жетеді.
Теорема. (Экстремумның бар болуының жеткілікті белгісі).
f(x) функциясы кризистік нүктесінің маңайында үзіліссіз болып, оның ойылған маңайында дифференциалдансын ( нүктесінен басқа нүктелерде) және аргумент кризистік нүктесінен солдан оңға қарай өткенде туынды таңбасын «+» тан «-» қа ауыстырса онда функция сол нүктеде максимумға жетеді, ал таңбасын «-» тан «-» қа ауыстырса минимумға жетеді.
Функцияның ең үлкен және ең кіші мәндерін табу.
[a,b] сегментінде үздіксіз y=f(x) функциясын қарастырайық. Мұндай функцияның өзінің ең үлкен және ең кіші мәніне сегменттен шеткі нүктелерінде не ішкі нүктелерінде жететіні белгілі. Егер ең үлкен (ең кіші) мәніне функция облыстың ішкі нүктесінде жетсе онда ол функцияның максимумы (минимумы) болады. Сонымен [a,b] сегментінде функцияның ең үлкен және ең кіші мәнін табудың төмендегідей ережесін аламыз.
1. 
интервалында функцияның барлық кризистік нүктелерін табамыз және сол нүктелердегі функция мәндерін табамыз.
2. Сегменттің шеткі х=а және х=в нүктелеріндегі функцияның мәндерін табамыз.
3. Барлық осы мәндердің ең үлкенін және ең кішісін аламыз.
Әдебиет
Қабдықайырұлы Қ. Жоғары математика. Алматы, «Қазақ университеті», 2004. (366-372 б.)
