Пусть на некотором этапе исследования выборки из возможных значений случайной величины возникает предположение (статистическая гипотеза) о распределении генеральной совокупности. Истинность основной (нулевой) гипотезы  проверятся в сравнении с альтернативными гипотезами
проверятся в сравнении с альтернативными гипотезами  ,
, 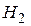 ,
,  , …. При этом, поскольку проверка осуществляется на основе выборки, а не всей генеральной совокупности, то все же существует, может и малая, вероятность того, что верная гипотеза будет отвергнута (ошибка 1-го рода), или наоборот принимается гипотеза, которая справедлива только для отдельной выборки и не справедлива для всей генеральной совокупности (ошибка 2-го рода). Поэтому гипотеза
, …. При этом, поскольку проверка осуществляется на основе выборки, а не всей генеральной совокупности, то все же существует, может и малая, вероятность того, что верная гипотеза будет отвергнута (ошибка 1-го рода), или наоборот принимается гипотеза, которая справедлива только для отдельной выборки и не справедлива для всей генеральной совокупности (ошибка 2-го рода). Поэтому гипотеза  принимается или отвергается с некоторой вероятностью (доверительной вероятностью), чаще всего 0,9, 0,95, 0,99 и т.д.
принимается или отвергается с некоторой вероятностью (доверительной вероятностью), чаще всего 0,9, 0,95, 0,99 и т.д.
Рассмотрим критерии согласия, которые применяются для проверки гипотез о том, что распределение изучаемой случайной величины подчиняется некоторому известному распределению, то есть, случайная величина x задана функцией распределения  .
.
Критерий Колмогорова
Пусть имеется выборка  значений случайной величины x, по которой строится эмпирическая функция распределения
значений случайной величины x, по которой строится эмпирическая функция распределения  . Предположим, что случайная величина x задается функцией распределения
. Предположим, что случайная величина x задается функцией распределения  .
.
Теорема. Если функция  непрерывна, то
непрерывна, то

где  , то есть, величина
, то есть, величина  определяет наибольшую меру отклонения эмпирической функции распределения
определяет наибольшую меру отклонения эмпирической функции распределения  от теоретической
от теоретической  .
.
Замечание. Из теоремы следует, что критерий Колмогорова применим для оценки только непрерывных и полностью определенных, включая параметры, распределений и при достаточно большом объеме статистических данных.
Пусть задана некоторая выборка, по которой на плоскости строится ломаная линия. В этой же системе координат строим график теоретической функции распределения.
Определяем  и полагаем
и полагаем  . Находим
. Находим  , где
, где  - вероятность того, что за счет случайных причин максимальный разброс
- вероятность того, что за счет случайных причин максимальный разброс  и
и  будет меньше, чем фактически наблюдаемый. Если
будет меньше, чем фактически наблюдаемый. Если  - мала (<0,2), то
- мала (<0,2), то  не соответствует опытным данным, если
не соответствует опытным данным, если  - велика (>0,2), то
- велика (>0,2), то  совместима с данными выборки.
совместима с данными выборки.
Критерий c2
Пусть задан интервальный статистический ряд распределения случайной величины x. По нему найдем теоретические вероятности  , соответствующие столбцу r,
, соответствующие столбцу r,  . Предположим, что случайная величина x задается функцией распределения
. Предположим, что случайная величина x задается функцией распределения  . За меру отклонения между распределением выборки и теоретическим распределением принимается сумма квадратов разности между теоретическими и опытными вероятностями:
. За меру отклонения между распределением выборки и теоретическим распределением принимается сумма квадратов разности между теоретическими и опытными вероятностями:
 ,
,
где  - некоторые коэффициенты.
- некоторые коэффициенты.
Если положить  , то закон распределения d не зависит от вида
, то закон распределения d не зависит от вида  , числа опытов n и асимптотически сходится к распределению c2,
, числа опытов n и асимптотически сходится к распределению c2,
 или
или 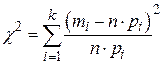 .
.
Распределение c 2 имеет  число степеней свободы, где k – число интервалов, на которые разбито множество наблюдений, r – число параметров теоретического распределения вероятностей.
число степеней свободы, где k – число интервалов, на которые разбито множество наблюдений, r – число параметров теоретического распределения вероятностей.
По выборке вычисляется величина  , которая сравнивается с
, которая сравнивается с  . Если
. Если  , то считается, что гипотеза не согласуется с наблюдаемыми значениями случайной величины, если
, то считается, что гипотеза не согласуется с наблюдаемыми значениями случайной величины, если  , то гипотеза не противоречит опытным данным.
, то гипотеза не противоречит опытным данным.
Замечание. Если критерий Колмогорова требует для своего применения жестких условий, то критерий c2 (Пирсона) либерален. Во-первых, он применяется при проверке гипотез как дискретных, так и непрерывных случайных величин, и, во-вторых, значения параметров могут быть вычислены из этих же статистических данных. Принято считать, что для применения критерия достаточно, чтобы  .
.






