1. Равномерное распределение на отрезке 
(для краткости говорят: X подчиняется закону 
) (см. рис.):
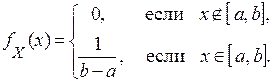(6)
Равномерное распределение реализуется в экспериментах, в которых наудачу ставится точка на отрезке (Х – абсцисса поставленной точки), а также в экспериментах по измерению тех или иных величин с округлением (Х – ошибка округления).
 |
0 
2. Показательное (экспоненциальное) распределение с параметром l (для краткости говорят: Х подчиняется закону 
):
(7)
Показательное распределение часто встречается в теории массового обслуживания (например, Х – время ожидания при техническом обслуживании или Х – длительность телефонных разговоров, ежедневно регистрируемых на телефонной станции) и в теории надежности (например, Х – срок службы радиоэлектронной аппаратуры).
3. Нормальный закон распределения. Случайная величина называется распределенной по нормальному (гауссовскому) закону с параметрами 
и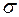 
> 0 если плотность распределения вероятностей имеет вид (см. рис.)
(8)
Параметры 
и 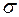совпадают с основными характеристиками распределения:
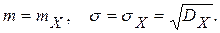
Для краткости говорят, что случайная величина Х распределена по закону
N (т, 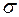), если ее плотность вероятностей записывается в виде (8). Если Х распределена по закону 
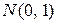, то она называется стандартизованной нормальной величиной. Функция распределения стандартизованной гауссовской величины имеет вид:
(9)
С ее помощью можно вычислять интервальные вероятности для нормального распределения N (т, 
):
(10)
Функцию распределения можно записать в виде 
, где 
- функция Лапласа. Имеются таблицы значений этой функции.
Для вероятности попадания на симметричный относительно математического ожидания интервал справедлива формула
(11)
В частности, 
, 
, 
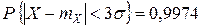(т. е. практически достоверно, что 
принимает свои значения в промежутке 
(«правило трех сигм»)).
Центральные моменты нормального распределения удовлетворяют рекуррентному соотношению
Отсюда следует, что все центральные моменты нечетного порядка для нормального распределения равны нулю (т. к. 
).
Пример. Случайная величина X подчиняется закону распределения Парето с параметрами > 0 и 
> 0, если она непрерывного типа и её функция распределения вероятностей имеет вид
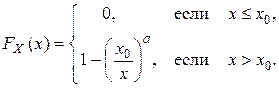(12)
Найти 
, 
, 
для распределения Парето, выразив их через параметры распределения.
◄ Находим плотность распределения вероятностей
Математическое ожидание вычисляем по формуле для случая непрерывной случайной величины:
Очевидно, математическое ожидание существует, если существует несобственный интеграл с бесконечным пределом, т. е. при > 1. В этом случае, вычисляя интеграл, получим
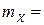
Для вычисления дисперсии используем формулу 
. Найдем второй начальный момент: 
(
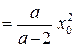). Отсюда
().
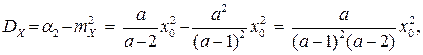Медиану находим как корень уравнения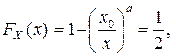 
откуда 
►
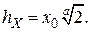