Приведем некоторые часто встречающиеся в вероятностных моделях законы распределения дискретных случайных величин.
1○. Биномиальный закон для числа успехов 
при 
независимых испытаниях в схеме Бернулли
{ X = 
} = 
, = 0, 1, …, n, (1)
где 
– параметр распределения, равный вероятности наступления успеха в каждом отдельном испытании. Соответствующее этой формуле Бернулли распределение случайной величины называется биномиальным распределением (или распределением Бернулли). Для краткости говорят, что распределено по закону 
.
Основные характеристики биномиального распределения:
mX = np, 
= npq, aX = 
, eX = 
.
Пример. Вероятности рождения девочки и мальчика в первом приближении можно считать равными 0,5. Какова вероятность того, что среди 
наудачу отобранных новорожденных будет хотя бы один мальчик (событие 
); число мальчиков и девочек одинаково (событие 
); мальчиков будет больше, чем девочек (событие 
)? Получить числовые значения искомых вероятностей для = 10.
◄ Пусть Х – число мальчиков среди новорожденных. Случайная величина Х подчиняется распределению 
, т.е. согласно формуле (1)
{ X = k } = 
, k = 0,1,…, .
Вероятность события проще всего найти, перейдя к противоположному событию:
() = 1 - (
) = 1 - { X = 0} = 1 - .
Вероятность события записывается непосредственно:
() = { X = n } = 
.
Для подсчета вероятности события заметим, что распределение Бернулли симметрично относительно значения 
. Действительно:
{ X = 
} = Р2n, n-k 
= 
= Р2n, n+k = { X = 
}
для всех k =1, 2,…, 
. Кроме того, нетрудно проверить, что это значение является наиболее вероятным, т.е. мода распределения dX = . В силу симметрии распределения выполняется равенство { X > } = { X < } =
= 
(1 - { X = }). Таким образом, () = (1 -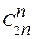 
).
Найдем числовые значения полученных вероятностей при = 10:
() = 1 – 
= 0,9990, () = 
= 0,2461,
() = (1 - ()) = 0,3770. ►
2. Равномерное распределение на {1, 2, …, N }:
{ X = } = 
, = 0, 1,…, N. (2)
3. Распределение Пуассона. Случайная величина Х называется распределенной по закону Пуассона с параметром 
> 0, если ее возможные значения равны 0, 1, 2,..., а соответствующие вероятности определяются формулой
(3)
Характерной особенностью распределения Пуассона является совпадение математического ожидания и дисперсии, причем
Распределение Пуассона может быть получено из биномиального распределения путем предельного перехода при 
при условии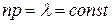 
и в этом случае интерпретируется как закон «редких» явлений. Если достаточно велико, а мало, то, как уже отмечалось ранее, формулу Пуассона (3) можно использовать в качестве приближения вместо точной биномиальной формулы для нахождения вероятностей успехов при независимых испытаниях.
Пример. На факультете насчитывается 500 студентов. Какова вероятность того,что 1 сентября является днем рождения одновременно для студентов данного факультета? Вычислить указанную вероятность для значений = 0, 1, 2, 3.
◄ Так как = 500 >> 1 и = {родиться 1 сентября любому из студентов факультета} = 
<< 1, то можно считать, что случайное число студентов X, родившихся 1 сентября, подчиняется закону распределения Пуассона с параметром 
= 1,36986. Поэтому по формуле (3) 
Далее находим рекуррентно:
Значения искомых вероятностей, соответствующих биномиальному распределению 
и вычисленных с четырьмя верными знаками после запятой, таковы: 
►
5. Геометрическое распределение зависит от параметра (0 < < 1) и определяется вероятностями
{ X = } = 
, = 0, 1, 2 …, 
= 1 – . (4)
В этом случае также выполнено условие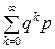 
= 1.
Пример. Производится стрельба по цели до первого попадания. Вероятность попадания при каждом выстреле равна . Найти математическое ожидание числа произведенных выстрелов, считая, что стрелять можно неограниченное число раз. Вычислить указанную величину при 
.
◄ Для случайного числа произведенных выстрелов ряд распределения имеет вид
|
| … | |||
| 
| 
| 
| … |
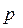
Из этого ряда видно, что имеет геометрическое распределение. Математическое ожидание находим по формуле для случая дискретной величины: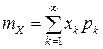 
= 
= 
= 
= = 
= 
= = 
. При имеем 
, т.е. среднее число выстрелов до первого попадания при данной вероятности попадания при каждом выстреле будет равно пяти. ►
