Из повседневного опыта известно, что одни случайные события наступают довольно часто, другие менее часто или совсем редко. Однако эти характеристики событий слишком неопределенны. Более объективной экспериментальной характеристикой случайного события (обозначим его, например, через 
) является относительная статистическая частота 
, равная отношению числа опытов 
, в которых событие наступило, к общему числу опытов 
, т. е. 
. Экспериментально установлено, что для многих событий относительная частота при увеличении становится почти постоянной. Это свойство называют статистической устойчивостью относительных частот. Таким образом, с каждым событием можно связать некоторое число 
, с которым сближается частота, и считать это число вероятностью события .
Рассмотренные выше и ряд других эмпирических фактов, связанных с поведением относительных частот наступления тех или иных событий в повторных испытаниях, обобщение этих фактов и абстрагирование свойств относительных частот привели к аксиоматическому определению понятия вероятности как меры возможности наступления того или иного наблюдаемого в опыте события.
Пусть 
– алгебра событий для данного опыта. Вероятностью называется числовая функция, определенная для всех 
и удовлетворяющая трем условиям (аксиомам вероятностей):
1) 
(аксиома неотрицательности);
2) 
(аксиома нормированности);
3) Если и 
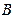несовместны (т. е. 
), то 
(аксиома аддитивности).
Нетрудно убедиться, что относительные частоты удовлетворяют условиям 1) – 3). Действительно,
, 
.
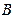Если реальные события и несовместны, то они наступили при разных опытах и, следовательно, 
. Отсюда
,
что соответствует 3).
Для решения задач, связанных с бесконечными последовательностями событий, требуется дополнить приведенные аксиомы следующей аксиомой:
4) Если в последовательности наблюдаемых событий 
события попарно несовместны (т. е. 
при 
) и 
, то 
(расширенная аксиома аддитивности).
Из аксиом 1) – 3) следует, что 
; в частности 
. Кроме того, если для некоторого опыта 
, то 
. Важно отметить, что из равенств 
или 
не следует, что событие является достоверным или соответственно невозможным.
Тройку 
, где – алгебра подмножеств множества элементарных исходов 
, 
– числовая функция, удовлетворяющая условиям 1) – 3), называют вероятностным пространством. Построение вероятностного пространства является основным этапом математической формализации того или иного случайного опыта. Наиболее трудной ее частью является задание вероятностного распределения на поле событий для данного опыта, которое в общем случае определяется следующим образом.
Пусть совокупность 
является разбиением множества . Тогда в силу аксиом 2) и 4) 
. Это значит, что единичная вероятность достоверного события распределяется по множеству несовместных событий, образующих полную группу. Соответствие между событиями некоторого поля и их вероятностями и называют распределением вероятностей.
Оставаясь в рамках аксиоматической теории, задачу о задании вероятностного распределения на поле событий для данного опыта нельзя решить однозначно. Вопрос о том, какое значение вероятности приписать тем или иным событиям в реальных опытах, решается методами математической статистики.
Знание вероятности наступления интересующего нас события позволяет предсказать с определенной точностью относительную частоту осуществления данного события при проведении достаточно большого числа реальных испытаний, т. е. вероятность выполняет прогностическую функцию. Задачи, которые решаются в теории вероятностей, заключаются в том, чтобы по вероятностям некоторых простых событий, известным из опыта, находить вероятности интересующих нас сложных событий. В других задачах вероятностное пространство строится на основе проведения аналогии между описываемым опытом и какой-либо моделью случайного опыта с известным распределением вероятностей. Ниже рассматриваются несколько важных частных моделей случайных явлений.
Конечное вероятностное пространство. Формула классической вероятности. Пусть 
– конечное множество элементарных исходов, 
– набор чисел, удовлетворяющих условиям
.
Вероятностью события назовем число , определенное формулой
,
где событие 
. Если 
, то по определению полагаем, что . Числа являются вероятностями элементарных исходов (элементарными вероятностями). Таким образом, вероятность события равна сумме тех элементарных вероятностей 
, у которых 
входят в . Нетрудно убедиться, что определенная таким образом вероятность удовлетворяет всем аксиомам вероятностей.
Определенное выше конечное вероятностное пространство называют также конечной схемой. В конечной схеме вероятность однозначно определяется элементарными вероятностями. Эта схема во многих случаях служит хорошей математической моделью случайных событий.
Рассмотрим частный случай конечной схемы, в котором элементарные вероятности одинаковы, т. е. множество представляет собой конечное множество равновероятных исходов: 
. Тогда победем иметь
, (1)
где 
– число элементов множества (число всех благоприятствующих событию исходов), 
– число элементов множества (число всех элементарных исходов опыта).
Определение (1) называют классическим определением вероятности, а саму формулу (1) – формулой классической вероятности.
Классическое определение вероятности является хорошей моделью тех случайных явлений, для которых элементарные исходы опыта обладают определенной симметрией по отношению к условиям опыта, так что нет оснований считать какой-либо из исходов более вероятным, чем другие. Обычно это предположение оправдано в задачах из области азартных игр, лотерей и т. д. Это объясняется тем, что при изготовлении игральных костей, карт, рулеток и организации лотерей заботятся о соблюдении равновозможности различных исходов. Такие же требования предъявляются к организации выборочного контроля и выборочных статистических исследований.
Пример. Из колоды в 36 карт наудачу вынимается одна карта. Какова вероятность вынуть карту пиковой масти?
◄ Здесь всего исходов 
. Событие ={вынута карта пиковой масти}. Число равновозможных исходов, благоприятствующих наступлению события , 
. Следовательно, 
. ►
Пример. Бросаются одновременно две симметричные монеты. Какова вероятность выпадения герба на обеих монетах?
◄ Множество состоит из 
равновозможных элементарных исходов: 
. Событию ={выпало два герба} благоприятствует 
исходов. По формуле классической вероятности получаем 
. ►
Непрерывное вероятностное пространство. Геометрические вероятности. Формула классической вероятности следующим образом обобщается на случай непрерывных множеств элементарных исходов .
Пусть – ограниченная замкнутая область на евклидовой плоскости, а условия опыта таковы, что вероятность попадания в произвольную подобласть области пропорциональна площади этой подобласти и не зависит от ее местоположения в . При этих условиях для вероятности наступления любого наблюдаемого в данном опыте события 
справедлива формула геометрической вероятности:
, (2)
где 
– площадь области , 
– площадь подобласти .
Формула (2) естественным образом обобщается на случай пространств произвольной размерности:
,
где 
– мера множества (длина, площадь, объем и т. д. в зависимости от размерности того пространства, в котором рассматриваются данные множества).
Пример. На обслуживающее устройство в промежуток времени 
должны поступить две заявки. Если разность между моментами поступления заявок меньше 
, то вторая заявка теряется. Найти вероятность потери заявки.
◄ Обозначим через 
и 
моменты поступления 1-й и 2-й заявок соответственно. Тогда множество можно записать в виде: 
. Искомое событие ={заявка будет потеряна} запишется в виде: 
. Если воспользоваться геометрически определением, то множества и изобразятся областями на плоскости, представленными на рис. 2. Площади этих фигур 
, 
. По формуле (2) находим 
. ►
