Рассмотрим издержки производства y как функцию количества выпускаемой продукции 
. Пусть 
– прирост продукции, 
– изменение издержек производства, тогда 
– среднее увеличение издержек производства на единицу продукции. Производная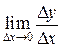 
выражает предельные издержки производства и приближено характеризует дополнительные затраты на производства единицы дополнительной продукции. Предельные издержки зависят от уровня производства и определяются не постоянными производственными затратами, а лишь переменными (на сырьё, топливо и т.д.). Аналогично могут быть определены предельная выручка, предельный доход, предельный продукт, предельная полезность.
Предельные величины характеризуют не состояние, а процесс, изменение экономического объекта. Таким образом, производная выступает как скорость изменения некоторого экономического объекта по времени или относительно другого исследуемого фактора.
Для исследования экономических процессов используется понятие эластичности функции.
Эластичность функции определяется так:
Это предел отношения относительного приращения функции к относительному приращению 
при 
.
Эластичность приближено показывает, на сколько процентов изменится функция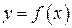 
при изменении на 
.
Свойства эластичности:
1. Эластичность функции равна произведению независимой переменной на темп изменения функций:
,
где темп изменения функции выражается по формуле:
2. Эластичность произведения (частного) двух функций равна сумме (разности) эластичностей этих функций:
Эластичность функции применяется при анализе спроса и потребления. Например, эластичность спроса у относительно цены x (или дохода x) – это коэффициент, показывающий приближенно, на сколько процентов изменится спрос (объём потребления) при увеличения цены (или дохода) на 1%.
Если 
, то функция называется эластичной, если 
– неэластичной, при 
функция называется нейтральной.
Еще одним примером использования производной в экономике является анализ производственной функции. Поскольку ограниченность ресурсов принципиально не устранима, то решающее значение приобретает отдача от факторов производства. Здесь также применима производная как инструмент исследования.
Пусть применяемый капитал постоянен, а затраты труда увеличиваются. Можно ввести в экономический анализ следующую категорию – предельный продукт труда MPL (marginal product of labor) – это дополнительный продукт 
, полученный в результате дополнительных вложений труда 
(L – labor) при неизменной величине капитала: 
. Если вложения осуществляются достаточно малыми порциями, то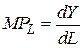 
. Т.к. dY – результат, dL – затраты, то MPL – предельная производительность труда.
Аналогично, 
– предельный продукт капитала – это дополнительный продукт, полученный в результате дополнительных вложений капитала 
при неизменной величине труда: 
. Если вложения осуществляются малыми порциями, то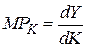 
. – характеризует предельную производительность капитала.
Пример. Опытным путём установлены функции спроса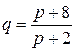 
и предложения 
, где q и s – количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени, p – цена товара. Найти: а) равновесную цену, т.е. цену при которой спрос равен предложению; б) эластичность спроса и предложения для этой цены; в) изменение дохода при увеличении цены на 5% от равновесной.
◄ а) Равновесная цена находится из условия q=s, тогда 
, откуда p= 2, т.е равновесная цена 2 ден.ед.
б) Найдём эластичность по спросу и предложению по формуле
. В нашем случае 
; 
. Для равновесной цены p=2 имеем 
; 
. Так как полученные значения эластичностей по абсолютной величине меньше 1, то и спрос и предложение данного товара при равновесной (рыночной) цене неэластичны относительно цены. Это означает, что изменение цены не приведёт к резкому изменению спроса и предложения. Так, при увеличении цены p на 1% спрос уменьшится на 0,3%, а предложение увеличится на 0,8%.
в) При увеличении цены p на 5% от равновесной спрос уменьшится на 5.0,3=1,5%, следовательно, доход возрастёт на 3,5%.►
Пример. Зависимость между издержками производства y и объёмом выпускаемой продукции x выражается функцией 
(ден.ед.). Определить средние и предельные издержки при объёме продукции 10 ед.
◄ Функция средних издержек выражается соотношением 
; при x= 10средние издержки (на единицу продукции) равны 
(ден. ед.). Функция предельных издержек выражается производной 
; при x= 10 предельные издержки составят 
(ден.ед.). Итак, если средние издержки на производство единицы продукции составляют 45 ден.ед., то предельные издержки, т.е. дополнительные затраты на производство дополнительной единицы продукции при данном уровне производства (объёме выпускаемой продукции 10 ед.), составляют 35 ден.ед. ►
